Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Hai đường thẳng song song khi:
- 2 góc so le trong bằng nhau.
- 2 góc đồng vị bằng nhau.
- 2 góc trong cùng phía bù nhau.
- Cùng song song với đường thẳng thứ 3.
- Cùng vuông góc với đường thẳng thứ 3
hai duong thang song song khi
2 góc sole bằng nhau
2 góc đồng vị bằng nhau
2 góc cùng phía bù nhau
cùng vuông góc với đng thắng thứ 3
cùng song song với đng thắng thứ 3

Có khá nhiều trg` hợp
Nếu 2 đường thẳng đó cùng song song với 1 đường thẳng khác
Nếu 2 đường thẳng đó cùng vuông góc với 1 đường thẳng khác
Nếu có 1 đùng thẳng căt qua và tạo thành :
+ 2 cặp góc so le trong bằng nhau
+ 2 cặp góc đồng vị bằng nhau
+ 2 cặp góc trong cùng phía bù nhau
Nều 2 đường thẳng đó là đấy và đường trung bình tương ứng
.....
- Hai đường thẳng song song khi:
+ Một cặp góc so le trong bằng nhau ;
+ Một cặp góc đồng vị bằng nhau ;
+ Một cặp góc trong cùng phía bù nhau ;
+ Cùng song song với đường thẳng thứ ba ;
+ Cùng vuông góc với đường thẳng thứ ba .

ta chứng minh nó là đồng vị,
kề bù,so le trong ,
trong cùng phía, ngoài cùng phía
từ đó ta sẽ pt hai đường thẳng đó có song song hay là vuông góc hay không
tíc mình nha

Vì đường thẳng AB cắt 2 đường thẳng a và b ,trong các góc tạo thánh có một cặp góc đọng vị bằng nhau thì a và b song song với nhau
Kẻ 1 dường thẳng khác và vuông góc với 2 đường thẳng đã cho => 2 đoạn thẳng đó song song

Lý Thuyết
1. Khoảng cách giữa hai đường thẳng song song
Định nghĩa: Khoảng cách giữa hai đường thẳng song song là khoảng cách từ một điểm tùy ý trên đường thẳng này đến đường thẳng kia. h là khoảng cách giữa hai đường thẳng song song a và b.
2. Tính chất của các điểm cách đều một đoạn thẳng cho trước.
Tính chất: Các điểm cách đường thẳng b một khoảng bằng h nằm trên hai đường thẳng song song với b và cách b một khoảng bằng h.
3. Đường thẳng song song cách đều
Định lí:
- Nếu các đường thẳng song song cách đều cắt một đường thằng thì chúng chắn trên đường thẳng đó các đoạn thẳng liên tiếp bằng nhau.
- Nếu các đường thẳng song song cắt một đường thẳng và chúng chắn trên đường thẳng đó các đoạn thẳng liên tiếp bằng nhau thì chúng song song cách đều.

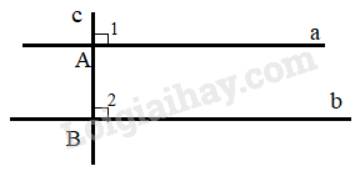
Giả sử có 2 đường thẳng phân biệt a,b cùng vuông góc với một đường thẳng c.
Ta có: \(\widehat {{A_1}} = \widehat {{B_2}}(=90^0)\), mà hai góc này ở vị trí đồng vị nên a//b (Dấu hiệu nhận biết 2 đường thẳng song song)
Như vậy, định lí trên có thể được suy ra trực tiếp từ định lí về dấu hiệu nhận biết hai đường thẳng song song.

Bài giải
a b A B 1 3 2 4
a, Nếu \(\widehat{A_1}=120^o\text{ ; }\widehat{B_3}=130^o\text{ }\text{thì }a\text{ không song song }b\)
Muốn \(a\text{ }//\text{ }b\text{ thì }\orbr{\begin{cases}\widehat{A_1}=\widehat{B_3}=130^o\\\widehat{A_1}=\widehat{B_3}=120^o\end{cases}}\) để hai góc bằng nhau ( so le ngoài )
b, Nếu \(\widehat{A_2}=65^o\text{ ; }\widehat{B_3}=64^o\) thì a không song song b
Muốn \(a\text{ }//\text{ }b\text{ thì }\orbr{\begin{cases}\widehat{A}_2=\widehat{B_3}=65^o\\\widehat{A_2}=\widehat{B_3}=64^o\end{cases}}\) để hai góc bằng nhau
CM 2 đường thẳng vuông góc:
1. Định lý: Nếu 1 đường thẳng vuông góc với 1 trong 2 đường thẳng song song thì nó cũng vuông góc với đường thẳng kia.
2. CM 2 đường thẳng đó tạo thành 1 góc 90o.
v..v....
CM 2 đường thẳng song song:
1. CM 2 đường thẳng đó cùng vuông góc với 1 đường thẳng thứ ba
2. CM 2 góc sole trong/ đồng vị/ sole ngoài bằng nhau
3. CM 2 góc trong cùng phía/ ngoài cùng phía bù nhau
các bn hiu nhầm câu hoi rùì
giả sử có 2 dg thg xy và cd, trên xy lấy AB,trên cd lay CD =AB
neu AD = BC thi chac chan xy//cd ( vi ABCD la hbh)