Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

\(\left[{}\begin{matrix}x=2\sqrt{2}\simeq2.82\\x=-2\sqrt{2}\simeq-2.82\end{matrix}\right.\)

x 2 = 6 ⇒ x 1 = 6 v à x 2 = - 6
Ta có: x 1 = 6 ≈ 2,449 và x 2 = -6 = -2,449

x 2 = 5 ⇒ x 1 = 5 v à x 2 = - 5
Ta có: x 1 = ( 5 ) = 1 , 495 v à x 2 = - ( 5 ) = - 1 , 495

x 2 = 5 ⇒ x 1 = 5 v à x 2 = - 5
Ta có: x 1 = 5 ≈ 2,236 và x 2 = - 5 = -2,236

x 2 = 2 , 5 ⇒ x 1 = 2 , 5 v à x 2 = - 2 , 5
Ta có: x 1 = 2 , 5 = 1 , 581 v à x 2 = - 2 , 5 = - 1 , 581

(2x - √2)2 – 1 = (x + 1)(x – 1);
⇔ 4x2 – 2.2x.√2 + 2 – 1 = x2 – 1
⇔ 4x2 – 2.2√2.x + 2 – 1 – x2 + 1 = 0
⇔ 3x2 – 2.2√2.x + 2 = 0
Có: a = 3; b’ = -2√2; c = 2; Δ’ = b’2 – ac = (-2√2)2 – 3.2 = 2 > 0
Vì Δ’ > 0 nên phương trình có hai nghiệm phân biệt là:
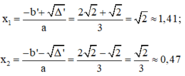

0,5x(x + 1) = (x – 1)2
⇔ 0,5x2 + 0,5x = x2 – 2x + 1
⇔ x2 – 2x + 1 – 0,5x2 – 0,5x = 0
⇔ 0,5x2 – 2,5x + 1 = 0
⇔ x2 – 5x + 2 = 0
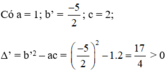
Phương trình có hai nghiệm phân biệt:
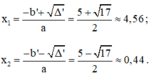

3x2 + 3 = 2(x + 1)
⇔ 3x2 + 3 = 2x + 2
⇔ 3x2 + 3 – 2x – 2 = 0
⇔ 3x2 – 2x + 1 = 0
Phương trình có a = 3; b’ = -1; c = 1; Δ’ = b’2 – ac = (-1)2 – 3.1 = -2 < 0
Vậy phương trình vô nghiệm.
