Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

bn mũ 3 lên đc bao nhiêu đã
sau đó p/t thành nhân tử đặt nhân tử chung
hok tốt

\(\sqrt{x^2-2x+4}+\sqrt{x^2+5}=9-2x\left(đk:x\le\dfrac{9}{2}\right)\)
\(\Leftrightarrow x^2-2x+4+x^2+5+2\sqrt{\left(x^2-2x+4\right)\left(x^2+5\right)}=81-36x+4x^2\)
\(\Leftrightarrow2\sqrt{\left(x^2-2x+4\right)\left(x^2+5\right)}=2x^2-34x+72\)
\(\Leftrightarrow4\left(x^2-2x+4\right)\left(x^2+5\right)=4x^4+1156x^2+5184-136x^3+288x^2-4896x\)
\(\Leftrightarrow4x^4-8x^3+36x^2-40x+80=4x^4-136x^3+1444x^2-4896x+5184\)
\(\Leftrightarrow128x^3-1408x^2+4856x-5104=0\)
\(\Leftrightarrow128x^2\left(x-2\right)-1152x\left(x-2\right)+2552\left(x-2\right)=0\)
\(\Leftrightarrow\left(x-2\right)\left(128x^2-1152x+2552\right)=0\)
\(\Leftrightarrow x=2\left(tm\right)\)(do \(128x^2-1152x+2552>0\))

\(\left(2\sqrt{6}-4\sqrt{3}+5\sqrt{2}\right)\cdot3\sqrt{6}\)
\(=2\sqrt{6}\cdot3\sqrt{6}-4\sqrt{3}\cdot3\sqrt{6}+5\sqrt{2}\cdot3\sqrt{6}\)
\(=36-36\sqrt{2}+30\sqrt{3}\)

A: Phần trắc nghiệm
Câu 1: B
Câu 2: A
Câu 3: C
Câu 4: D
Câu 5: B
Câu 6: A
Câu 7: C
Câu 8: A
Câu 9: D
Câu 10: A

Sửa đề : \(\sqrt{x+3-4\sqrt{x-1}}+\sqrt{x+8-6\sqrt{x-1}}=1\) (*)
ĐK : \(\left\{{}\begin{matrix}x-1\ge0\\x-3-4\sqrt{x-1}\ge0vàx+8-6\sqrt{x-1}\ge0\end{matrix}\right.\)(*) \(\Leftrightarrow\sqrt{\left(x-1\right)-2.2\sqrt{x-1}+4}+\sqrt{\left(x-1\right)-2.3\sqrt{x-1}+9}=1\)
\(\Leftrightarrow\sqrt{\left(\sqrt{x-1}-2\right)^2}+\sqrt{\left(\sqrt{x-1}-3\right)^2}=1\)
\(\Leftrightarrow\left|\sqrt{x-1}-2\right|+\left|\sqrt{x-1}-3\right|=1\)
=================
Đến đây phá dấu giá trị tuyệt đối ra rồi giải tiếp , bn tự làm nhé

\(\sqrt{2x+\sqrt{4x-1}}+\sqrt{2x-\sqrt{4x-1}}=\sqrt{6}\)
(ĐKXĐ: \(x\ge\dfrac{1}{4}\))
\(\Leftrightarrow2x+\sqrt{4x-1}+2x-\sqrt{4x-1}+2\sqrt{4x^2-4x+1}=6\)
\(\Leftrightarrow4x+2\sqrt{\left(2x-1\right)^2}=6\)
\(\Leftrightarrow2\left(2x+\left|2x-1\right|\right)=6\)
\(\Leftrightarrow2x+\left|2x-1\right|=3\)
\(\Leftrightarrow\left|2x-1\right|=3-2x\)
\(\Leftrightarrow\left[{}\begin{matrix}3-2x\ge0\\2x-1=3-2x\\2x-1=2x-3\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x\le\dfrac{3}{2}\\x=1\left(nhận\right)\\0=-2\left(vô.lý\right)\end{matrix}\right.\)
Vậy phương trình đã cho có nghiệm là x=1.

a: ĐKXĐ: \(x>0\)
b: Ta có: \(A=\dfrac{x^2+\sqrt{x}}{x-\sqrt{x}+1}-\dfrac{2x+\sqrt{x}}{\sqrt{x}}+1\)
\(=x+\sqrt{x}-2\sqrt{x}-1+1\)
\(=x-\sqrt{x}\)
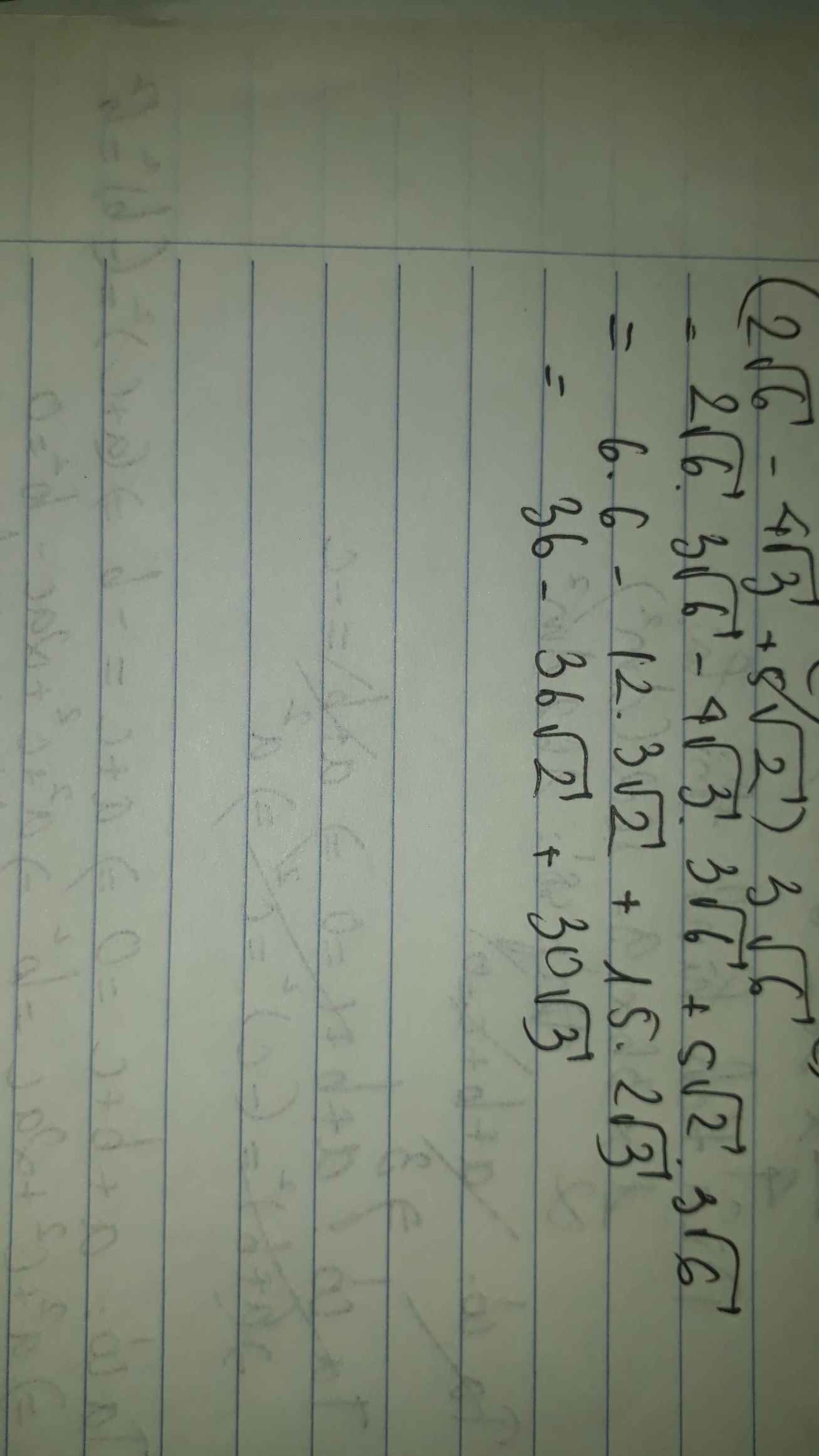


Ta có: \(\sqrt{2x+7}-6=x\)
\(\Leftrightarrow\sqrt{2x+7}=x+6\)
\(\Leftrightarrow x^2+12x+36-2x-7=0\)
\(\Leftrightarrow x^2+10x+29=0\)(Vô lý)
Vậy: \(S=\varnothing\)
Điều kiện : x ≥ 0
\(\sqrt{2x+97}-6=x\text{⇔}\sqrt{2x+97}=x+6\\ \text{⇔}2x+97=x^2+12x+36\text{⇔}x^2+10x-61=0\\ \text{⇔}\left[{}\begin{matrix}x=-5+\sqrt{86}\\x=-5-\sqrt{86}\end{matrix}\right.\)