
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

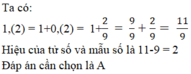

Tử và mẫu có tổng = 18 nên :
18 = 2 + 16 = 3 + 15 = 4 +14 = 5 + 13 = 6 + 12 = 7 + 11 = 8 + 10 = 9 + 9.
Do phân số tối giản nên có thể chọn 15 cặp:
\(\frac{5}{13}\) hoặc \(\frac{7}{11}\)

b)Phân số 5/8 được viết dưới dạng số thập phân hữu hạn vì có mẫu 8 = 23 không có ước nguyên tố khác 2 và 5
– Phân số-3/20 được viết dưới dạng số thập phân hữu hạn vì có mẫu 20 = 22 . 5 không có ước nguyên tố khác 2 và 5
– Phân số 14/35 được viết dưới dạng số thập phân hữu hạn vì14/35 = 2/5, mẫu 5 không có ước nguyên tố khác 2 và 5
– Các phân số 4/11 ; 15/22 ; 7/12 có mẫu lần lượt là 11 = 1 . 11; 22 = 2 . 11; 12 = 3 . 22 đều chứa ước nguyên tố khác 2 và 5 nên được viết dưới dạng số thập phân vô hạn tuần hoàn.
- 5/8 = 0,625; −3/20 = -0,15; 14/35 = 2/5 = 0,4 4/11 = 0,(36); 15/22 = 0,6(81); 7/12 = 0,58(3)
a) lấy máy tính để đổi nhé

Giải thích: Các phân số đã cho có mẫu dương và các mẫu đó lần lượt là 8 = 23, 5, 20 = 22.5, 125 = 53 đều không chứa thừa số nguyên tố nào khác 2 và 5 nên chúng được viết dưới dạng số thập phân hữu hạn.
3/8 = 0,375 ; −7/5 = -1,4; 13/20 = 0,65 ; −13/125 = -0,104
b. Các phân số đã cho có mẫu dương và các mẫu đó lần lượt là 12=22.3, 22=2.11, 35=7.5, 65 = 5.13 đều có chứa thừa số nguyên tố khác 2 và 5 nên chúng được viết dưới dạng số thập phân vô hạn tuần hoàn
ta được : \(\frac{5}{12}=0.41\left(6\right);\frac{29}{22}=1.3\left(18\right);\frac{27}{35}=0.7;\frac{51}{65}=0.8\)

1) Vì mẫu của chúng không chứa ước nguyên tố khác 2 và 5:
3/8 có mẫu 8 = 2^3
-7/5 có mẫu 5 = 5
13/20 có mẫu 20 = 2^2 . 5
-13/125 có mẫu 125 = 5^3
Nên: các phân số trên viết được dưới dạng số thập phân hữu hạn
Ta có: 3/8 = 0,375
-7/5 = -1,4
13/20 = 0,65
-13/125 = -0,104

a) \(C=\frac{m^3+3m^2+2m+5}{m\left(m+1\right)\left(m+2\right)+6}\)
\(C=\frac{m^3+2m^2+m^2+2m+5}{m\left(m+1\right)\left(m+2\right)+6}\)
\(C=\frac{m^2.\left(m+2\right)+m.\left(m+2\right)+5}{m\left(m+1\right)\left(m+2\right)+6}\)
\(C=\frac{\left(m+2\right).\left(m^2+m\right)+5}{m\left(m+1\right)\left(m+2\right)+6}\)
\(C=\frac{\left(m+2\right).m.\left(m+1\right)+5}{m\left(m+1\right)\left(m+2\right)+6}=\frac{a}{a+1}\)
Gọi d = ƯCLN(a; a + 1) (d \(\in\) N*)
\(\Rightarrow\begin{cases}a⋮d\\a+1⋮d\end{cases}\) \(\Rightarrow\left(a+1\right)-a⋮d\)
\(\Rightarrow1⋮d\)
Mà d \(\in\) N* => d = 1
=> ƯCLN(a; a + 1) = 1
=> C là phân số tối giản (đpcm)
b) Ta thấy: m.(m + 1).(m + 2) là tích 3 số nguyên liên tiếp nên\(m\left(m+1\right)\left(m+2\right)⋮3\)
Mà \(5⋮̸3\); \(6⋮3\)
\(\Rightarrow\begin{cases}\left(m+2\right).m.\left(m+1\right)+5⋮̸3\\m\left(m+1\right)\left(m+2\right)+6⋮3\end{cases}\)
Như vậy, đến khi tối giản, phân số C vẫn có tử \(⋮3;\ne2;5\) nên phân số C viết được dưới dạng số thập phân vô hạn tuần hoàn.