
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Ta có:
\(\left(\dfrac{1}{10}\right)^{15}=\left(\left(\dfrac{1}{10}\right)^3\right)^5=\left(\dfrac{1}{1000}\right)^5\)
\(\left(\dfrac{3}{10}\right)^{20}=\left(\left(\dfrac{3}{10}\right)^4\right)^5=\left(\dfrac{81}{10000}\right)^5\)
Ta có: \(\left(\dfrac{1}{10}\right)^{15}=\left(\dfrac{1}{10}^3\right)^5=\left(\dfrac{1}{1000}\right)^5\)
\(\left(\dfrac{3}{10}\right)^{20}=\left(\dfrac{3}{10}^4\right)^5=\left(\dfrac{3}{10000}\right)^5\)
Vì \(\dfrac{1}{1000}>\dfrac{3}{10000}\) nên \(\left(\dfrac{1}{10}\right)^{15}>\left(\dfrac{3}{10}\right)^{20}\)


Ta có: \(\dfrac{4^7\cdot2^8}{3\cdot2^{15}\cdot16^2-5\cdot2^2\cdot\left(2^{10}\right)^2}\)
\(=\dfrac{2^{22}}{3\cdot2^{15}\cdot2^8-5\cdot2^2\cdot2^{20}}\)
\(=\dfrac{2^{22}}{2^{22}\left(3\cdot2-5\right)}\)
\(=1\)

a. \(\frac{15^3.\left(-5\right)^4}{\left(-3\right)^5.5^6}=\frac{3^3.5^3.5^4}{\left(-3\right)^5.5^6}\)
\(=\frac{3^3.5^7}{\left(-3\right)^5.5^6}=\frac{5}{-9}\)
b. \(\frac{6^3.2^5.\left(-3\right)^2}{\left(-2\right)^9.3^7}=\frac{2^3.3^3.2^5.3^2}{\left(-2\right)^9.3^7}\)
\(=\frac{2^8.3^5}{\left(-2\right)^9.3^7}=\frac{1}{\left(-2\right).3^2}=-\frac{1}{18}\)

Bài làm
Đặt a - b = x ; b - c = y ; c - a = z
=> x + y + z = 0
Ta có :
\(N=\left(\frac{1}{x}+\frac{1}{y}+\frac{1}{z}\right)^2-2.\left(\frac{1}{xy}+\frac{1}{yz}+\frac{1}{xz}\right)=\left(\frac{1}{x}+\frac{1}{y}+\frac{1}{z}\right)^2-2.\left(\frac{x+y+z}{xyz}\right)\)
=> \(N=\left(\frac{1}{x}+\frac{1}{y}+\frac{1}{z}\right)^2\)( Vì x + y + z = 0 )
Vậy ta có đpcm

a) ta có A=\(15^{120}:25^{60}=3^{120}.5^{120}:5^{120}=3^{120}=9^{60}\)
B=\(2^{45}.2^{15}.4^{60}=2^{60}.2^{120}=2^{180}=8^{60}\)
-> A<B
b) bạn chỉ cần tính từng cái ra là dc ý ,ak dễ lắm nếu bạn chăm chỉ

\(\left(\frac{27}{64}\right)^{15}=\frac{\left(3^3\right)^{15}}{\left(2^6\right)^{15}}=\frac{3^{45}}{2^{90}}=\left(\frac{3}{2^2}\right)^{45}\)
\(\left(\frac{81}{256}\right)^{10}=\frac{\left(3^4\right)^{10}}{\left(2^8\right)^{10}}=\frac{3^{40}}{2^{80}}=\left(\frac{3}{2^2}\right)^{40}\)
Do \(\left(\frac{3}{2^2}\right)^{45}
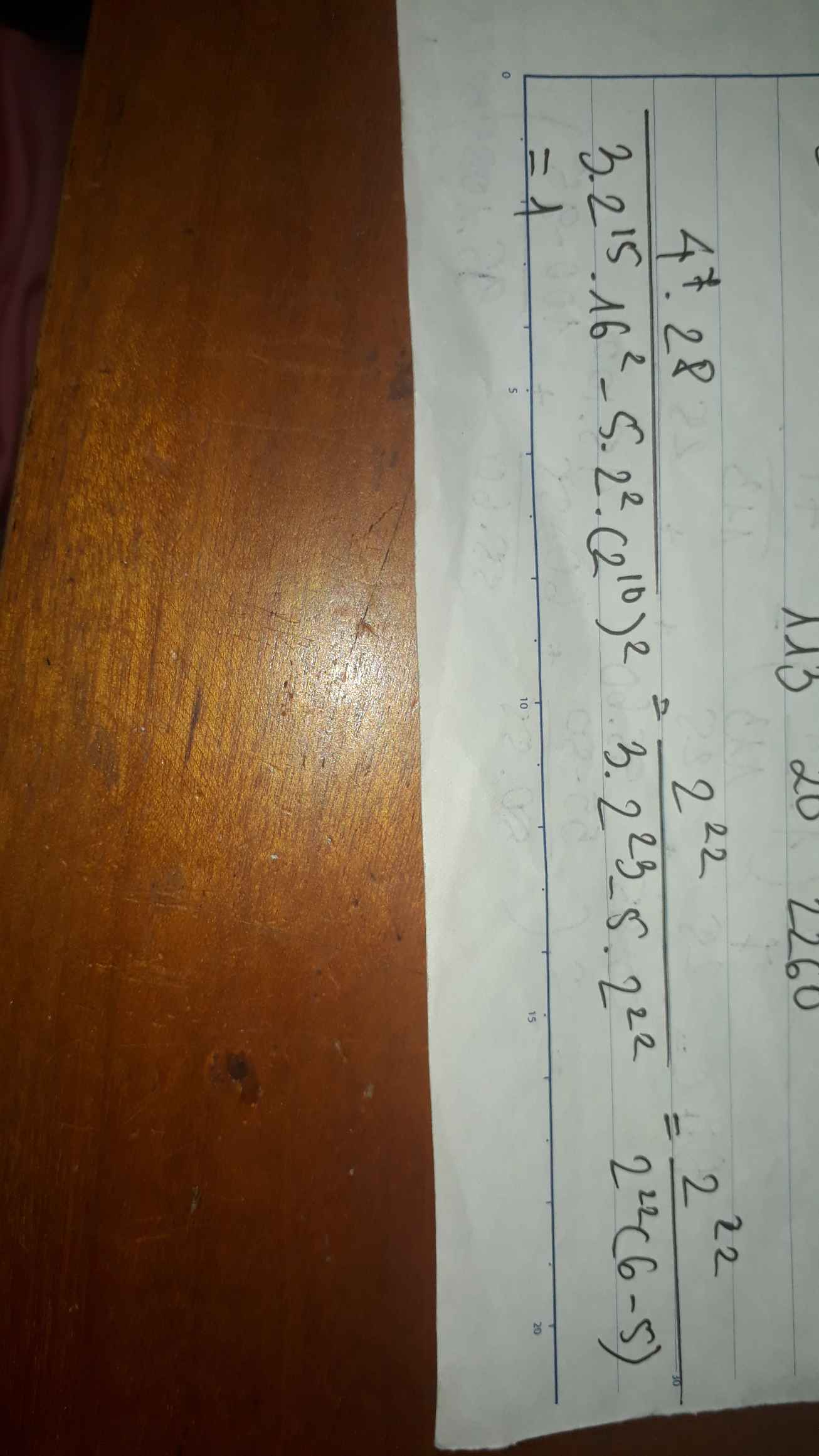
Ta có: \({\left( {{{15}^3}} \right)^2}\) = 153 . 153 = 153+3 = 156
\({15^{3.2}}\) = 156
Vậy \({\left( {{{15}^3}} \right)^2}\) = \({15^{3.2}}\)