So sánh: $\dfrac{x-y}{x+y}$ và $\dfrac{x^2-y^2}{x^2+xy+y^2}$ với x>y>0

Khách

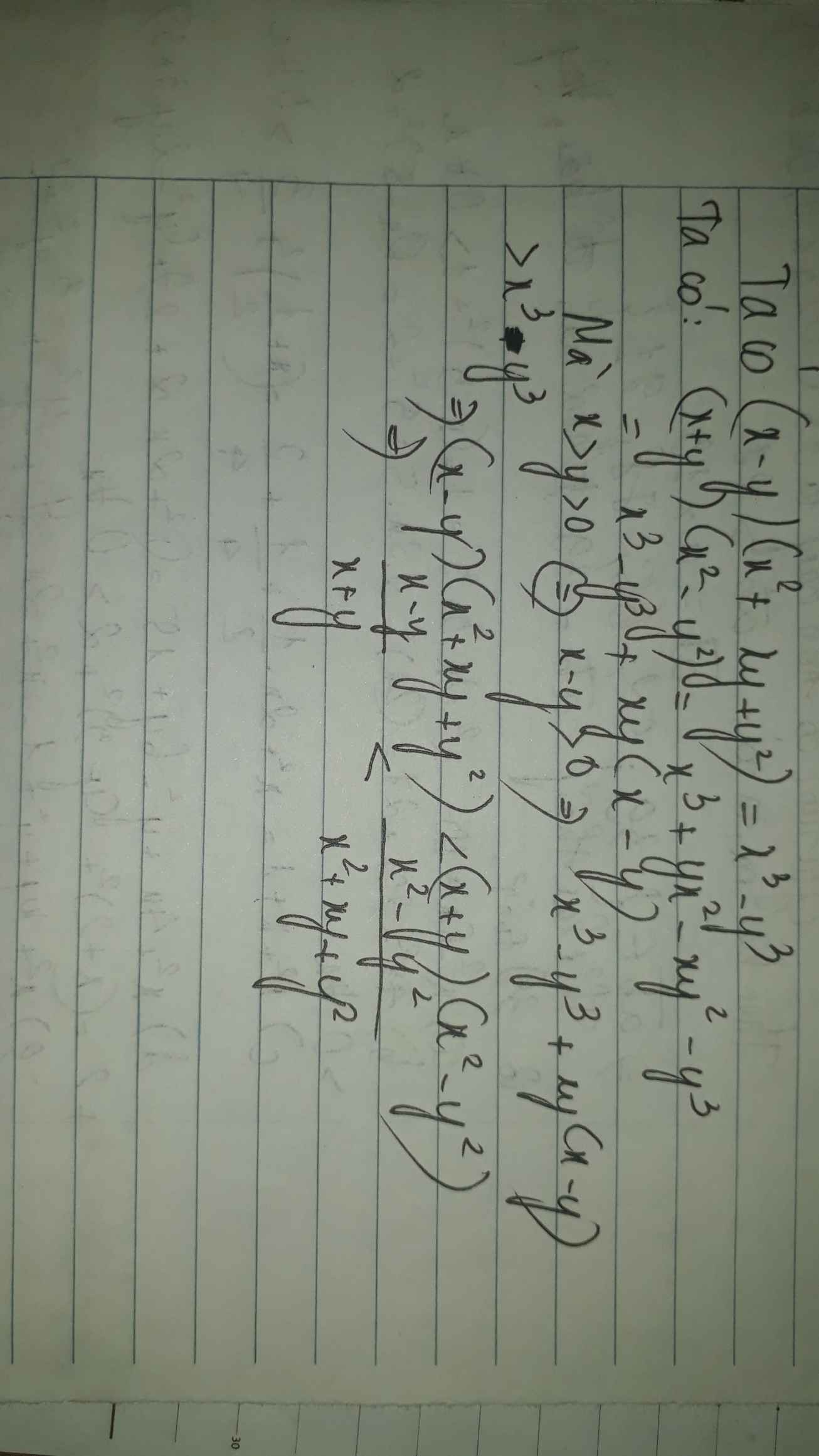
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Chọn lớp

Chọn môn

Mua vip

Phuong Anh Do

10 tháng 8 2021

So sánh: $\dfrac{x-y}{x+y}$ và $\dfrac{x^2-y^2}{x^2+xy+y^2}$ với x>y>0

#Toán lớp 8

Trên con đường thành công không có....

10 tháng 8 2021

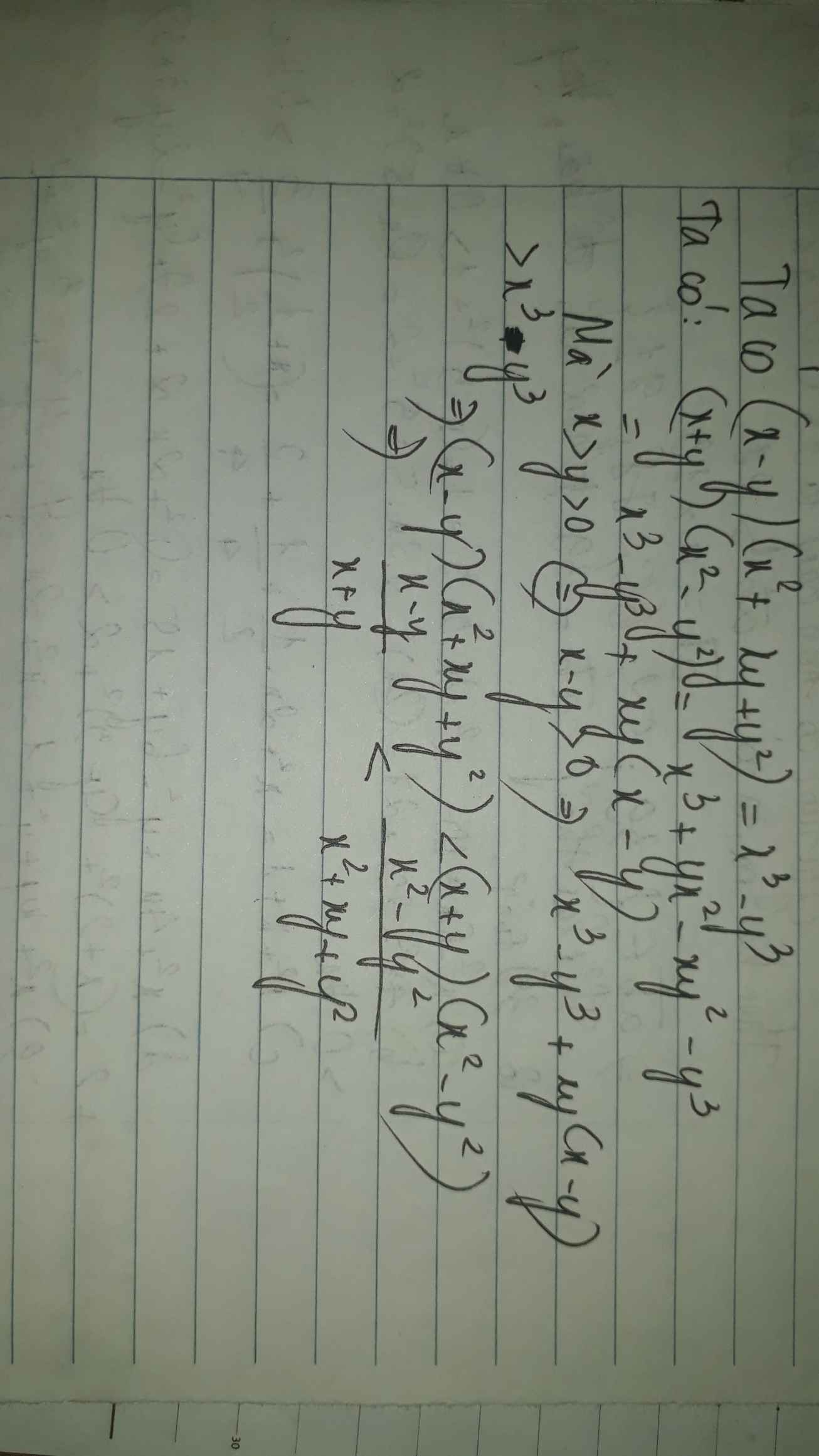
undefined

Đúng(3)

Các câu hỏi dưới đây có thể giống với câu hỏi trên

tư

9 tháng 3 2016 - olm

cho x>y>0

so sánh A= (x-y)/(x+y) và B=(x^2-y^2)/(x^2+y^2) 1like cho bạn giúp mik với mik cần gấp

#Toán lớp 8

Ngọc Nhi

13 tháng 2 2018

1. Cho các số dương x,y thỏa mãn : x2010 + y2010= x2011 + y2011 = x2012 + y2012. Tính x2016 + y2016. 2.Tìm các số x,y thỏa mãn : 2x2 + y2 -2y = 2(xy-1) 3.Cho y>x>0 và $\dfrac{x^2+y^2}{xy}=\dfrac{10}{3}$. Tính giá trị biểu thức: A= $\dfrac{x-y}{x+y}$ 4. Cho phân thức $P=\dfrac{x^2+2y^2}{2x+3y+4}$. Với giá trị nào của x và y thì P=0. ...

Đọc tiếp

#Toán lớp 8

Hoàng Anh Thư

13 tháng 2 2018

theo đầu bài ta có$\dfrac{x^2+y^2}{xy}=\dfrac{10}{3}$=>$3x^2+3y^2=10xy$

A=$\dfrac{x-y}{x+y}$

=>$A^2=\left(\dfrac{x-y}{x+y}\right)^2=\dfrac{x^2-2xy+y^2}{x^2+2xy+y^2}=\dfrac{3x^2-6xy+3y^2}{3x^2+6xy+3y^2}=\dfrac{10xy-6xy}{10xy+6xy}=\dfrac{4xy}{16xy}=\dfrac{1}{4}$

=>A=$\sqrt{\dfrac{1}{4}}=\dfrac{-1}{2}hoặc\sqrt{\dfrac{1}{4}}=\dfrac{1}{2}$ (cộng trừ căn 1/4 nhé)

vì y>x>0=> A=-1/2

Đúng(0)

Trần Thuận Ngân

22 tháng 3 2021

Cho xy≠0, chứng minh rằng $\dfrac{x^2}{y^2}+\dfrac{y^2}{x^2}$≥$\dfrac{x}{y}+\dfrac{y}{x}$

#Toán lớp 8

Nguyễn Việt Lâm

Giáo viên

22 tháng 3 2021

BĐT cần chứng minh tương đương:

$x^4+y^4\ge x^3y+xy^3$

$\Leftrightarrow x^4-x^3y+y^4-xy^3\ge0$

$\Leftrightarrow x^3\left(x-y\right)-y^3\left(x-y\right)\ge0$

$\Leftrightarrow\left(x-y\right)\left(x^3-y^3\right)\ge0$

$\Leftrightarrow\left(x-y\right)^2\left(x^2+xy+y^2\right)\ge0$ (luôn đúng)

Vậy BĐT đã cho đúng

Đúng(3)

ntkhai0708

22 tháng 3 2021

Ta có bất đẳng thức $a^2+b^2 \geq \dfrac{(a+b)^2}{2}

$⇔2.(a^2+b^2) \geq (a+b)^2$

$⇔(a-b)^2 \geq 0$ (đúng)

Áp dụng bất đẳng thức trên cho $\dfrac{x}{y}$ và $\dfrac{y}{x}$ có:

$\dfrac{x^2}{y^2}+\dfrac{y^2}{x^2} $

$\geq \dfrac{(\dfrac{x}{y}+\dfrac{y}{x})^2}{2}$

Hay $2.\dfrac{x^2}{y^2}+\dfrac{y^2}{x^2} \geq (\dfrac{x}{y}+\dfrac{y}{x})^2$

Áp dụng bất đẳng thức Cauchy (Cô-si) có:

$\dfrac{x}{y}+\dfrac{y}{x} \geq 2.\sqrt[]{\dfrac{x}{y}.\dfrac{y}{x}}=2$

Nên $(\dfrac{x}{y}+\dfrac{y}{x}).(\dfrac{x}{y}+\dfrac{y}{x}) \geq 2.(\dfrac{x}{y}+\dfrac{y}{x})$

Hay $ (\dfrac{x}{y}+\dfrac{y}{x})^2 \geq 2.(\dfrac{x}{y}+\dfrac{y}{x})$

Suy ra $2.\dfrac{x^2}{y^2}+\dfrac{y^2}{x^2} \geq 2.(\dfrac{x}{y}+\dfrac{y}{x})$

Hay $\dfrac{x^2}{y^2}+\dfrac{y^2}{x^2} \geq (\dfrac{x}{y}+\dfrac{y}{x})(đpcm)$

Dấu $=$ xảy ra $⇔x=y$

Đúng(0)

Thơ Nụ =))

18 tháng 1

cho 2 số thực `x,y` thỏa mãn `x>0,y>2,x`$\ne$`2y`. CMR: $\left(\dfrac{x-y}{2y-x}-\dfrac{x^2+y^2+y-2}{x^2-xy-2y^2}\right)\left(2x^2+y+2\right):\dfrac{x^4+4x^2y^2+y^4-4}{x^2+y+xy+x}=\dfrac{x+1}{2y-x}$

#Toán lớp 8

Nguyễn Việt Lâm

Giáo viên

19 tháng 1

Đề bài sai, đề đúng thì phân thức đằng sau dấu chia phải là:

$\dfrac{4x^4+4x^2y+y^2-4}{x^2+y+xy+x}$

Đúng(0)

Yuki Nguyễn

28 tháng 1 2019

Cho biểu thức: ( với x;y ≠ 0 ; x ≠ - y )

$P=\dfrac{2}{x}-\left(\dfrac{x^2}{x^2+xy}+\dfrac{y^2-x^2}{xy}-\dfrac{y^2}{xy+y^2}\right).\dfrac{x+y}{x^2+xy+y^2}$

a) Rút gọn P

b) Tìm giá trị của P biết x; y thỏa mãn: x² +y² + 10 = 2(x - 3y )

#Toán lớp 8

Nguyễn Việt Lâm

Giáo viên

28 tháng 1 2019

ĐKXĐ: $...$

$P=\dfrac{2}{x}-\left(\dfrac{x^2}{x\left(x+y\right)}-\dfrac{y^2}{y\left(x+y\right)}+\dfrac{y^2-x^2}{xy}\right).\dfrac{x+y}{x^2+xy+y^2}$

$P=\dfrac{2}{x}-\left(\dfrac{x-y}{x+y}-\dfrac{\left(x-y\right)\left(x+y\right)}{xy}\right).\dfrac{x+y}{x^2+xy+y^2}$

$P=\dfrac{2}{x}-\left(\dfrac{1}{x+y}-\dfrac{x+y}{xy}\right)\dfrac{x^2-y^2}{x^2+xy+y^2}$

$P=\dfrac{2}{x}-\dfrac{-\left(x^2+xy+y^2\right)}{xy\left(x+y\right)}.\dfrac{\left(x-y\right)\left(x+y\right)}{x^2+xy+y^2}$

$P=\dfrac{2}{x}+\dfrac{x-y}{xy}=\dfrac{2}{x}+\dfrac{1}{y}-\dfrac{1}{x}=\dfrac{1}{x}+\dfrac{1}{y}$

b/ $x^2+y^2+10=2x-6y\Leftrightarrow x^2-2x+1+y^2+6y+9=0$

$\Leftrightarrow\left(x-1\right)^2+\left(y+3\right)^2=0\Leftrightarrow\left\{{}\begin{matrix}x=1\\y=-3\end{matrix}\right.$

$\Rightarrow P=\dfrac{1}{1}-\dfrac{1}{3}=\dfrac{2}{3}$

Đúng(0)

Đinh Cẩm Tú

17 tháng 4 2021

Rút gọn biểu thức:

$\dfrac{x^2+xy}{x^2+xy+y^2}$ - [$\dfrac{x\left(2x^2+xy-y^2\right)}{x^3-y^3}$ - 2 + $\dfrac{y}{y-x}$] : $\dfrac{x-y}{x}$ - $\dfrac{x}{x-y}$

#Toán lớp 8

Nguyễn Lê Phước Thịnh

17 tháng 4 2021

Ta có: $\dfrac{x^2+xy}{x^2+xy+y^2}-\left(\dfrac{x\left(2x^2+xy-y^2\right)}{x^3-y^3}-2+\dfrac{y}{y-x}\right):\dfrac{x-y}{x}-\dfrac{x}{x-y}$

$=\dfrac{x^2+xy}{x^2+xy+y^2}-\left(\dfrac{x\left(2x^2+xy-y^2\right)}{\left(x-y\right)\left(x^2+xy+y^2\right)}-\dfrac{2\left(x^3-y^3\right)-y\left(x^2+xy+y^2\right)}{\left(x-y\right)\left(x^2+xy+y^2\right)}\right):\dfrac{x-y}{x}-\dfrac{x}{x-y}$

$=\dfrac{x^2+xy}{x^2+xy+y^2}-\dfrac{2x^3+x^2y-xy^2-2x^3+2y^3-x^2y-xy^2-y^3}{\left(x-y\right)\left(x^2+xy+y^2\right)}:\dfrac{x-y}{x}-\dfrac{x}{x-y}$

$=\dfrac{x\left(x+y\right)}{x^2+xy+y^2}-\dfrac{y^3-2xy^2}{\left(x-y\right)\left(x^2+xy+y^2\right)}:\dfrac{x-y}{x}-\dfrac{x}{x-y}$

$=\dfrac{x\left(x+y\right)}{x^2+xy+y^2}+\dfrac{y^2\left(x-y\right)}{\left(x-y\right)\left(x^2+xy+y^2\right)}\cdot\dfrac{x}{x-y}-\dfrac{x}{x-y}$

$=\dfrac{x\left(x+y\right)}{x^2+xy+y^2}+\dfrac{xy^2}{\left(x-y\right)\left(x^2+xy+y^2\right)}-\dfrac{x}{x-y}$

$=\dfrac{x\left(x^2-y^2\right)}{\left(x-y\right)\left(x^2+xy+y^2\right)}+\dfrac{xy^2}{\left(x-y\right)\left(x^2+xy+y^2\right)}-\dfrac{x\left(x^2+xy+y^2\right)}{\left(x-y\right)\left(x^2+xy+y^2\right)}$

$=\dfrac{x^3-xy^2+xy^2-x^3-x^2y-xy^2}{\left(x-y\right)\left(x^2+xy+y^2\right)}$

$=\dfrac{-x^2y-xy^2}{\left(x-y\right)\left(x^2+xy+y^2\right)}$

Đúng(0)

Tiến Hoàng Minh

11 tháng 1 2022

Cho x,y là hai số thay đổi thoat mãn x>0,y<0,x+y=1

A=$\dfrac{\text{y}-x}{\text{xy}}:\left(\dfrac{y^2}{\left(x-y\right)^2}-\dfrac{2x^2y}{\left(x^2-y^2\right)^2}+\dfrac{x^2}{y^2-x^2}\right)$

a) Rút gọn A

b) cmr A<-4

#Toán lớp 8

Nguyệt Trần

23 tháng 1 2017

Cho A=$(\dfrac{x}{y^2+xy}-\dfrac{x-y}{x^2+xy}):(\dfrac{y^2}{x^3-xy^2}+\dfrac{1}{x+y}):\dfrac{x}{y}$

a)tìm tập xác định của A

b)tìm x,y để A>1 và y<0

#Toán lớp 8

Nguyệt Trần

24 tháng 1 2017

Cho A=$(\dfrac{x}{y^2+xy}-\dfrac{x-y}{x^2+xy}):(\dfrac{y^2}{x^3-xy^2}+\dfrac{1}{x+y}):\dfrac{x}{y}$

a)tìm tập xác định của A

b)tìm x,y để A>1 và y<0

#Toán lớp 8

Nguyễn Quang Định

24 tháng 1 2017

tập xác định là gì

Đúng(0)

Nguyệt Trần

24 tháng 1 2017

mình cũng không biết, cô ghi sao mình ghi vậy

Đúng(0)

Chúng tôi đề xuất

Tài nguyên

Ứng dụng mobile

Bảng xếp hạng

Các khóa học có thể bạn quan tâm

Yêu cầu VIP