So sánh các góc của tam giác MNP, biết rằng MN = 8cm, NP = 3 cm, MP = 10 cm.

Khách

Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Chọn lớp

Chọn môn

Mua vip

Pham Trong Bach

13 tháng 5 2019

So sánh các góc của tam giác MNP, biết rằng MN = 8cm, NP = 3 cm, MP = 10 cm.

#Toán lớp 7

Cao Minh Tâm

13 tháng 5 2019

Đúng(0)

Các câu hỏi dưới đây có thể giống với câu hỏi trên

baek huyn

5 tháng 3 2018 - olm

Tam giác MNP có MN = 5cm , NP = 7cm , Mp =8cm . So sánh các góc của tam giác MNP

#Toán lớp 7

I don't need you

5 tháng 3 2018

XÉT \(\Delta MNP\)

CÓ: \(MP>NP>MN\left(8cm>7cm>5cm\right)\)

\(\Rightarrow\widehat{N}>\widehat{M}>\widehat{P}\)( ĐỊNH LÍ : TRONG 1 TAM GIÁC, GÓC ĐỐI DIỆN VỚI CẠNH LỚN HƠN LÀ GÓC LỚN HƠN)

CHÚC BN HỌC TỐT!!!!

Đúng(0)

Trinh

28 tháng 4 2022

Cho tam giác MNP biết MN=4cm,NP=5cm,MP=6cm. So sánh các góc của tam giác MNP

#Toán lớp 7

Kiệt Hoàng

28 tháng 4 2022

Đối diện cạnh MN là góc P

Đối diện cạnh NP là góc M

Đối diện cạnh MP là góc NMà MP>NP>MN(6cm>5cm>4cm)=>góc N>M>P

Đúng(3)

Tryechun🥶

28 tháng 4 2022

\(MP>NP>MN\\ \Rightarrow N>M>P\)

Đúng(3)

Đặng Nọc Long

29 tháng 4 2022

Cho tam giác MNP có MN = 6cm, MP = 8cm cm, NP = 10 cm.
a) Chứng minh tam giác MNP là tam giác vuông
b) Vẽ tia phân giác góc N cắt MP tại D, từ D vẽ DE vuông góc với ND. Chứng minh DM = DE
c) ED cắt MN tai F. Chứng minh tam giác MDF = tam giác EDP

#Toán lớp 7

Nguyễn Lê Phước Thịnh

30 tháng 4 2022

a: Xét ΔMNP có \(NP^2=MP^2+MN^2\)

nên ΔMNP vuông tại M

b: Xét ΔNMD vuông tại M và ΔNED vuông tại E có

ND chung

\(\widehat{MND}=\widehat{END}\)

DO đó: ΔNMD=ΔNED

Suy ra: DM=DE

Đúng(0)

Hoàng đức

13 tháng 3 2022

Cho tam giác MNP,MN>MP>NP. So sánh các góc của tam giác

#Toán lớp 7

Chuu

13 tháng 3 2022

Ta có: MN>MP>NP

=>góc P> góc N> góc M ( định lí: trong 1 tam giác góc đối diện với cạnh lớn hơn là góc lớn hơn

Đúng(1)

Shinichi Kudo

13 tháng 3 2022

Xét \(\Delta MNP\) có :

MN>MP>NP

=> \(\widehat{P}>\widehat{N}>\widehat{M}\)

Đúng(1)

Đoàn Thu Hiền

12 tháng 3 2018 - olm

Cho tam giác MNP có MN= 5cm, NP= 7cm , MP= 8cm. So sánh độ dài ba góc MNP

#giúpmknha

#Toán lớp 7

Girl

12 tháng 3 2018

Thực hiện so sánh các cạnh: \(MN< NP< MP\)

Dựa vào tích chất cạnh và góc đối diện trong tam giác: \(\widehat{P}< \widehat{M}< \widehat{N}\)

Đúng(1)

Đoàn Thu Hiền

12 tháng 3 2018

Thanksbn nha!!!!!!

Đúng(0)

Quoc Tran Anh Le

Giáo viên

19 tháng 9 2023

Cho tam giác MNP có độ dài các cạnh MN = 3 cm, NP = 5 cm, MP = 7 cm. Hãy xác định góc đối diện với từng cạnh rồi sắp xếp các góc của tam giác MNP theo thứ tự từ bé đến lớn.

#Toán lớp 7

Kiều Sơn Tùng

19 tháng 9 2023

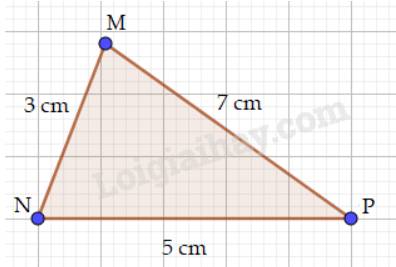
Góc P đối diện với cạnh MN

Góc M đối diện với cạnh NP

Góc N đối diện với cạnh MP.

Ta có: MN < NP < MP nên \(\widehat P < \widehat M < \widehat N\)( định lí)

Vậy sắp xếp các góc của tam giác MNP theo thứ tự từ bé đến lớn là: \(\widehat P;\widehat M;\widehat N\).

Đúng(0)

Quoc Tran Anh Le

Giáo viên

17 tháng 9 2023

Cho tam giác MNP có \(MN = 4\)cm, \(NP = 5\)cm, \(MP = 6\) cm. Tìm góc nhỏ nhất, góc lớn nhất của tam giác MNP.

#Toán lớp 7

Kiều Sơn Tùng

17 tháng 9 2023

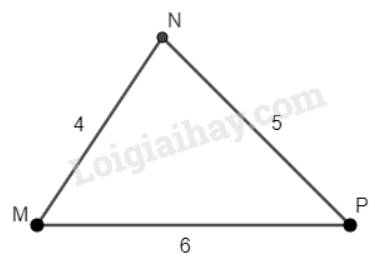
Trong tam giác MNP: \(MN < NP < MP\).

\(\Rightarrow\) Cạnh MN nhỏ nhất, MP lớn nhất trong tam giác MNP.

Vậy góc nhỏ nhất của tam giác MNP là góc P (đối diện với cạnh MN), góc lớn nhất của tam giác MNP là góc N (đối diện với cạnh MP)

Đúng(0)

Char

10 tháng 3 2022

Cho tam giác MNP cân tại A có MN = MP = 5 cm ; NP= 8cm

Kẻ MH vuông góc với NP (H thuộc NP).

a. Chứng minh HN = HP và

b. Tính độ dài MH

c. Kẻ HD vuông góc MN (D thuộc MN) Kẻ HE vuông góc MP (E thuộc MP).Chứng minh DHDE là tam giác cân.

#Toán lớp 7

Nguyễn Lê Phước Thịnh

11 tháng 3 2022

a: ta có: ΔMNP cân tại M

mà MH là đường cao

nên H là trung điểm của NP

hay HN=HP

b: NH=NP/2=8/2=4(cm)

=>MH=3(cm)

c: Xét ΔMDH vuông tại D và ΔMEH vuông tại E có

MH chung

\(\widehat{DMH}=\widehat{EMH}\)

Do đó: ΔMDH=ΔMEH

Suy ra: HD=HE

hay ΔHED cân tại H

Đúng(0)

THTA gaming TV

24 tháng 2 2022

tam giác MNP góc M = 90 độ, MN = 6cm, NP= 10 cm

a) tính MP

b) kẻ MK vuông góc với NP

so sánh MK với MP

c) so sánh NK và KP

#Toán lớp 7

Nguyễn Huy Tú

24 tháng 2 2022

a, Theo định lí Pytago tam giác MNP vuông tại M

\(MP=\sqrt{NP^2-MN^2}=8cm\)

b, Ta có MK < MP ( cạnh huyền > cạnh góc vuông tam giác MKP vuông tại K)

Đúng(1)

Chúng tôi đề xuất

Tài nguyên

Ứng dụng mobile

Bảng xếp hạng

Các khóa học có thể bạn quan tâm

Yêu cầu VIP