
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


\(g,4=2^2;6=2.3\\ \Rightarrow BCNN\left(4,6\right)=2^2.3=12\\ \Rightarrow x\in BC\left(4,6\right)=B\left(12\right)=\left\{0;12;24;36;48;60;...\right\}\\ \text{Mà }0< x< 50\\ \Rightarrow x\in\left\{12;24;36;48\right\}\\ h,12=2^2.3;18=2.3^2\\ \Rightarrow BCNN\left(12,18\right)=2^2.3^2=36\\ \Rightarrow x\in BC\left(12,18\right)=B\left(36\right)=\left\{0;36;72;108;144;180;216;252;...\right\}\\ \text{Mà }x< 250\\ \Rightarrow x\in\left\{0;36;72;108;144;180;216\right\}\)
g,\(x⋮4,x⋮6\Rightarrow x\in BC\left(4,6\right)=\left\{\pm0;\pm12;\pm24;\pm36;\pm48;\pm60;...\right\}\)
Mà \(0< x< 50\Rightarrow x\in\left\{12;36;48\right\}\)
h,\(x⋮12,x⋮18\Rightarrow x\in BC\left(12,18\right)=\left\{0;\pm36;\pm72;\pm108;\pm144;\pm180;\pm216;\pm252;...\right\}\)
Mà \(x< 50\Rightarrow x\in\left\{0;\pm36;\pm72;\pm108;\pm144;\pm180;\pm216\right\}\)

A = 1 . 2 + 2 . 3 + 3 . 4 + 4 . 5 + ... + 98 . 99
3A = 1 . 2 . 3 + 2 . 3 . 3 + 3 . 4 . 3 + 4 . 5 . 3 + ... + 98 . 99 . 3
3A = 1 . 2 . 3 + 2 . 3 . ( 4 - 1 ) + 3 . 4 . ( 5 - 2 ) + 4 . 5 . ( 6 - 3 ) + ... + 98 . 99 . ( 100 - 97 )
3A = 1 . 2 . 3 + 2 . 3 . 4 - 1 . 2 . 3 + 3 . 4 . 5 - 2 . 3 . 4 + 4 . 5 . 6 - 3 . 4 . 5 + ... + 98 . 99 . 100 - 97 . 98 . 99
3A = 98 . 99 . 100
A = \(\frac{98.99.100}{3}\)
A = 323400

chia 2 trường hợp
mik bt lm nhưng ko đánh đc dấu nên xin lỗi nha
a)<=> 12=!2x-1!
vô nghiệm VT chẵn VP luôn lẻ
b)
2x-1=x+3=> 2x-x=3+1=4=> x=4
2x-1=-x-2=> 2x+x=-2+1=-1=> vô nghiệm

Ta có:
452 chia a dư 32
321 chia a dư 21
Suy ra a thuộc
Vì
Vậy số tự nhiên a đó là 60.

Ta có:
\(B=2\cdot\left(1\cdot99+2\cdot98+...+50\cdot50\right)-50\cdot50\)
\(=2\cdot\left(1\cdot99+2\cdot\left(99-1\right)+...+50\cdot\left(99-49\right)\right)-50\cdot50\)-
\(=2\cdot\left(1\cdot99+2\cdot99-1\cdot2+...+50\cdot99-49\cdot50\right)-50\cdot50\)
\(=2\cdot\left(\left(1\cdot99+2\cdot99+...+50\cdot99\right)-\left(1\cdot2+2\cdot3+...+49\cdot50\right)\right)-50\cdot50\)
\(=2\cdot\left(\frac{99\cdot50\cdot51}{2}-\frac{49\cdot50\cdot51}{3}\right)-50\cdot50\)
\(=2\cdot84575-2500\)
\(=166650\)
Vậy B=166650
A=1.99+2.98+3.97+...+97.3+98.2+99.1
A=1.99+2.(99−1)+3.(99−2)+...+98.(99−97)+99.(99−98)
A=1.99+2.99−1.2+3.99−2.3+98.99−97.98+99.99−98.99
=(1.99+2.99+3.99+...+98.99+99.99)−(1.2+2.3+3.4+...+97.98+98.99)
=99.(1+2+3+...+98+99)−(1.2+2.3+3.4+...+97.98+98.99)
=99.4950−(1.2+2.3+3.4+97.98+98.99)
Mà 1.2+2.3+3.4+...97.98+98.99
= 1/3 .[1.2+2.3.(4−1)+3.4.(5−2)+98.99.(100−97)]
=1/3.98.99.100
=323400
⇒A=99.4950−323400=166650
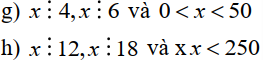 các bạn giải thích rõ ràng giúp mik nhé, cảm ơn các bạn nhiều
các bạn giải thích rõ ràng giúp mik nhé, cảm ơn các bạn nhiều
ta có A= 100100+1/100101+1< 1
-> 100100+1/100101+1 < 100100+1+99/ 100101+1+99= 100100+100/100101+100= 100(10099+1)/ 100(100100+1) = 10099+1/100100+1 =B
-> A<B
B1: so sánh 1 phân số vs 1 ( lưu í so sánh phân số có lũy thừa lớn hơn phân số có lũy thừa còn lại)
B2: suy ra phân số đó sẽ nhỏ hơn chính bằng phân số đó +99 để đc = 100 như phần số nguyên( nếu phần nguyên là 10 thì + 9, là 7 thì + 6 .....)
B3: đặt phần nguyên làm thừa số chung sau đó sẽ ra kq giống như phân số còn lại mà ta chưa so sánh
kết quả là A<B hoặc B<A
Ta có :
\(A=\frac{100^{100}+1}{100^{101}+1}\)
\(\Rightarrow100A=\frac{100^{101}+100}{100^{101}+1}\)
\(\Rightarrow100A=1+\frac{99}{100^{101}+1}\)
lại có :
\(B=\frac{100^{99}+1}{100^{100}+1}\)
\(\Rightarrow100B=\frac{100^{100+100}}{100^{100}+1}\)
\(\Rightarrow100B=1+\frac{99}{100^{100}+1}\)
Vì \(1+\frac{99}{100^{101}+1}< 1+\frac{99}{100^{100}+1}\Rightarrow100A< 100B\)
\(\Rightarrow A< B\)