DH
8
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
CM
16 tháng 4 2019
+ Lan viết đúng, vì :
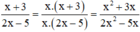
(Nhân cả tử và mẫu với x)
+ Hùng viết sai vì :
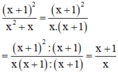
+ Giang viết đúng vì :
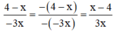
+ Huy viết sai vì :
CM
4 tháng 5 2018
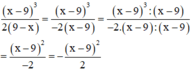
Nhân cả hai vế của bất đẳng thức a + 1 ≤ b + 2 với 2 > 0 ta được
2(a + 1) ≤ 2(b + 2) Û 2a + 2 ≤ 2b + 4.
Đáp án cần chọn là: D
CM
16 tháng 5 2019
Nhân cả hai vế của bất đẳng thức a - 2 ≤ b - 1 với 2 > 0 ta được:
2(a - 2) ≤ 2(b - 1) Û 2a - 4 ≤ 2b - 2.
Đáp án cần chọn là: D
NA
7
10 tháng 3 2018
\(a+b+c\ge3\sqrt[3]{3}\)
\(\frac{1}{a}+\frac{1}{b}+\frac{1}{c}\ge3\sqrt[3]{\frac{1}{abc}}\)
Nhân 2 vế ta được: \(\left(a+b+c\right).\left(\frac{1}{a}+\frac{1}{b}+\frac{1}{c}\right)\ge9\)
\(\Rightarrow\frac{1}{a}+\frac{1}{b}+\frac{1}{c}\ge\frac{9}{a+b+c}\)
Vậy \(\frac{1}{a}+\frac{1}{b}+\frac{1}{c}\ge\frac{9}{a+b+c}\left(đpcm\right)\)
10 tháng 3 2018
Nhân 2 vế vs a b c , xog r nhân hết ra pên vế traj ,
xog lấy tử chja mẫu sẽ đc 3 a/b b a c/b b/c a/c c/a ,
từg kặp số trên >=2 ,
cộg vao pag 3 2.3=9
13 tháng 11 2019
Bạn Trương who A,B,C,D để tìm đáp án sai hả cậu :)
Nhưng tớ có đáp án đúng :P mong cậu không chê hình của tớ và tớ không chắc đâu :)
N M C P B A D
Áp dụng hệ quả của định lý Ta-lét ta có :
-Do AD // BP nên \(\frac{AN}{NP}=\frac{AD}{BP}\)
-Do DC // AB nên \(\frac{DM}{AB}=\frac{ND}{NB}\)
Ta có : \(\frac{MC}{DM}=\frac{MD}{AM}\) mà \(\frac{MP}{AM}=\frac{CD}{BC}\Rightarrow\frac{MC}{DM}=\frac{PC}{CB}\)
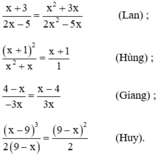
em chắc chắn số 5
so 8 em nghi zay
k nha