Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

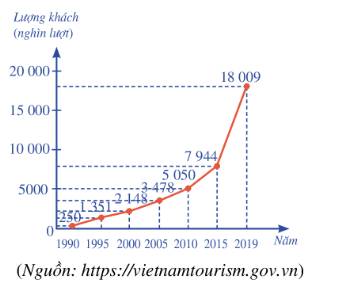
a) Mẫu số liệu thống kê số lượt khách du lịch Lượng khách quốc tế đến Việt Nam nhận được từ biểu đồ bên là:
250 1351 2148 3478 5050 7944 18009
b) Sắp xếp mẫu số liệu theo thứ tự không giảm ta được: 250 1351 2148 3478 5050 7944 18009
Số trung bình cộng của mẫu số liệu trên là:
\(\overline x = \frac{{250{\rm{ + }}1351{\rm{ + }}2148{\rm{ + }}3478{\rm{ + }}5050{\rm{ + }}7944{\rm{ + }}18009}}{7} = \frac{{38230}}{7}\)
Trung vị của mẫu số liệu trên là: Do mẫu số liệu trên có 7 số liệu ( lẻ ) nên trung vị \({Q_2} = 3478\)
Tứ phân vị của mẫu số liệu trên là:
- Trung vị của dãy 250 1351 2148 là: \({Q_1} = 1351\)
- Trung vị của dãy 5050 7944 18009 là: \({Q_3} = 7944\)
- Vậy tứ phân vị của mẫu số liệu là: \({Q_1} = 1351\), \({Q_2} = 3478\), \({Q_3} = 7944\)
c) Khoảng biến thiên của mẫu số liệu trên là: \(R = {x_{\max }} - {x_{\min }} = 18009 - 250 = 17759\)
Khoảng tứ phân vị của mẫu số liệu trên là: \({\Delta _Q} = {Q_3} - {Q_1} = 7944 - 1351 = 6593\)
d) Phương sai của mẫu số liệu trên là:
\({s^2} = \frac{{\left[ {{{\left( {250 - \overline x } \right)}^2} + {{\left( {351 - \overline x } \right)}^2} + ... + {{\left( {18009 - \overline x } \right)}^2}} \right]}}{7} \approx 31820198,82\)
Độ lệch chuẩn của mẫu số liệu trên là: \(s = \sqrt {{s^2}} \approx 5640,93\)

Chọn B.
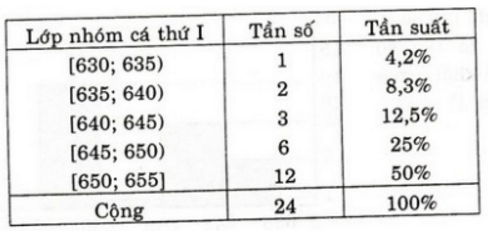
Ta có bảng phân bố tần số - tần suất
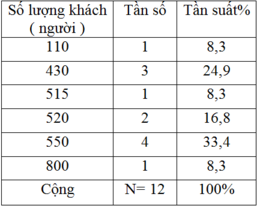
Dựa vào bảng phân bố tần số; tần suất ta thấy tần suất thấp nhất là 8,3%.

Chọn A.
| Tháng | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Số khách | 430 | 550 | 430 | 520 | 550 | 515 | 550 | 110 | 520 | 430 | 550 | 880 | Cộng: 6035 |
Đơn vị điều tra: Số khách đến tham quan một điểm du lịch trong 12 tháng
Kích thước mẫu của số liệu: 6035

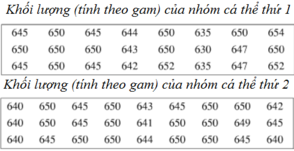
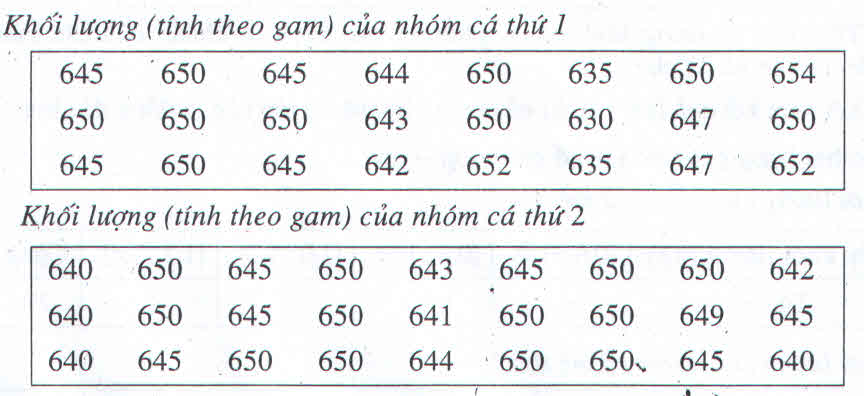
a) Bảng phân bố tần số và tần suất:
| Nhóm cá thứ I | Tần số | Tần suất |
|---|---|---|
| [630;635) | 1 | 4,2% |
| [635;640) | 2 | 8,3% |
| [640;645) | 3 | 12,5% |
| [645;650) | 6 | 25% |
| [650;655] | 12 | 50% |
| Cộng | 24 | 100% |
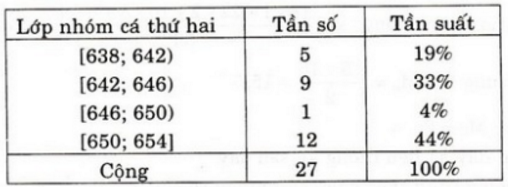
b) Bảng phân bố tần số và tần suất:
| Nhóm cá thứ I | Tần số | Tần suất |
|---|---|---|
| [638;642) | 5 | 18,52% |
| [642;646) | 9 | 33,33% |
| [646;650) | 1 | 3,7% |
| [650;654) | 12 | 44,45% |
| Cộng | 27 | 100% |
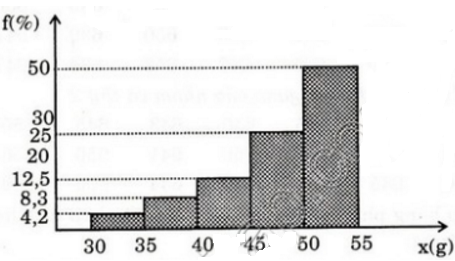
c) Biểu đồ tần suất hình cột:
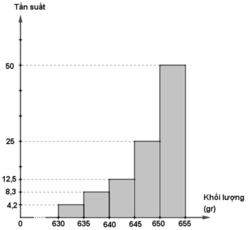
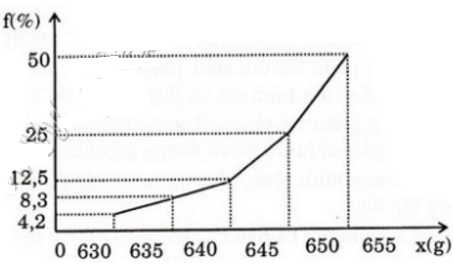
- Đường gấp khúc tần suất
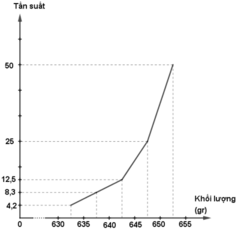
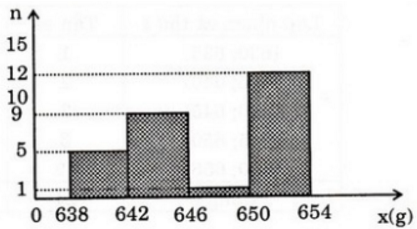
d) Biểu đồ tần số
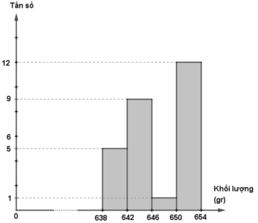
- Đường gấp khúc tần số
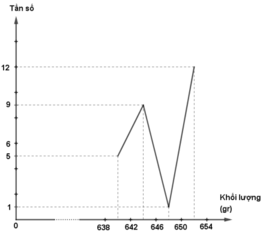
e) * Xét bảng phân bố ở câu a)
- Số trung bình:
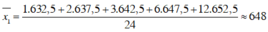
- Phương sai:
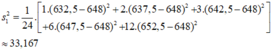
- Độ lệch chuẩn:
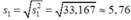
* Xét bảng phân bố ở câu b):
- Số trung bình:
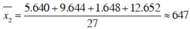
- Phương sai:
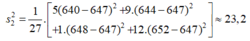
- Độ lệch chuẩn:
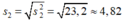
Nhận thấy s2 < s1 nên nhóm cá thứ hai có khối lượng đồng đều hơn.

a) Số điểm mà năm vận động viên bóng rổ ghi được trong một trận đấu:
9 8 15 8 20
Số trung bình: \(\overline X = \dfrac{{9 + 8 + 15 + 8 + 20}}{5} = 12\)
Trung vị:
Sắp xếp theo thứ tự không giảm:
8 8 9 15 20
Ta có n=5 là số lẻ nên trung vị là 9.
Mốt: Ta thấy số 8 là số có tần số cao nhất (xuất hiện 2 lần)
Tứ phân vị:
+ Tìm \({Q_2}\)
Ta có trung vị là 9=> \({Q_2} = 9\).
+ Tìm \({Q_1}\)
Nửa số liệu bên trái là:
8 8
Trung vị của mẫu này là \(\dfrac{{8 + 8}}{2} = 8\)=>\({Q_1} = 8\)
+ Tìm \({Q_3}\)
Nửa số liệu bên phải là:
15 20
Trung vị của mẫu này là \(\dfrac{{15 + 20}}{2} = 17,5\)=>\({Q_3} = 17,5\)
Vậy số trung bình là 12, trung vị là 9 và mốt là 8, \({Q_1} = 8\), \({Q_3} = 17,5\)
b) Giá của một số loại giày (đơn vị nghìn đồng):
350 300 650 300 450 500 300 250
Số trung bình: \(\overline X ) \( = \dfrac{{350 + 300.3 + 650 + 450 + 500 + 250}}{8}\) \( = 387,5\)
Trung vị:
Sắp xếp theo thứ tự không giảm:
250 300 300 300 350 450 500 650
Ta có n=8 là số chẵn nên trung vị là trung bình cộng của hai số chính giữa.
Hai số chính giữa là 300 và 350
=> Trung vị là \(\dfrac{{300 + 350}}{2} = 325\)
Mốt: Ta thấy số 300 là số có tần số cao nhất (xuất hiện 3 lần)
Tứ phân vị:
+ Tìm \({Q_2}\)
Ta có trung vị là 325=> \({Q_2} = 325\).
+ Tìm \({Q_1}\)
Vì n chẵn nên nửa số liệu bên trái là:
250 300 300 300
Trung vị của mẫu này là \(\dfrac{{300 + 300}}{2} = 300\)=>\({Q_1} = 300\)
+ Tìm \({Q_3}\)
Vì n chẵn nên nửa số liệu bên phải là:
350 450 500 650
Trung vị của mẫu này là \(\dfrac{{450 + 500}}{2} = 475\)=>\({Q_3} = 475\)
Vậy số trung bình là 387,5, trung vị là 325 và mốt là 300, \({Q_1} = 300\), \({Q_3} = 475\)
c) Số kênh được chiếu của một số hãng truyền hình cáp:
36 38 33 34 32 30 34 35
Số trung bình: \(\overline X = \dfrac{{36 + 38 + 33 + 34.2 + 32 + 30 + 35}}{8} = 34\)
Trung vị:
Sắp xếp theo thứ tự không giảm:
30 32 33 34 34 35 36 38
Ta có n=8 là số chẵn nên trung vị là trung bình cộng của hai số chính giữa.
Hai số chính giữa là 34 và 34
=> Trung vị là 34
Mốt: Ta thấy số 34 là số có tần số cao nhất (xuất hiện 2 lần)
Tứ phân vị:
+ Tìm \({Q_2}\)
Ta có trung vị là 34=> \({Q_2} = 34\).
+ Tìm \({Q_1}\)
Vì n chẵn nên nửa số liệu bên trái là:
30 32 33 34
Trung vị của mẫu này là \(\dfrac{{32 + 33}}{2} = 32,5\)=>\({Q_1} = 32,5\)
+ Tìm \({Q_3}\)
Vì n chẵn nên nửa số liệu bên phải là:
34 35 36 38
Trung vị của mẫu này là \(\dfrac{{35 + 36}}{2} = 35,5\)=>\({Q_3} = 35,5\)
Vậy số trung bình là 34, trung vị là 34 và mốt là 34, \({Q_1} = 32,5\), \({Q_3} = 35,5\)
Chú ý
Nếu n chẵn thì nửa số liệu bên trái (phải) \({Q_2}\) phải chứa cả \({Q_2}\)



c) Trong 35 ngày đến trường của bạn A, ta thấy :
- Chiếm tỉ lệ thấp nhất (11,43%) là những ngày bạn A có thời gian đến trường từ 27 phút đến 29 phút (ứng với cột thấp nhất của biểu đồ)
- Chiếm tỉ lệ cao nhất (28,57%) là những ngày bạn A có thời gian đến trường từ 23 phút đến dưới 25 phút (ứng với cột cao nhất của biểu đồ)
- Đa số các ngày (74,28%), bạn A có thời gian đến trường từ 21 phút đến dưới 27 phút (ứng với 3 cột cao trội lên của biểu đồ)

a) Bảng phân bố tần số và tần suất:
b) Bảng phân bố tần số và tần suất:
c) Biểu đồ tần suất hình cột:
- Đường gấp khúc tần suất
d) Biểu đồ tần số
- Đường gấp khúc tần số
e) Xét bảng phân bố ở câu a)
- Số trung bình cộng:
Từ đó ta thấy nhóm cá thứ 2 có khối lượng đồng đều hơn.

a)
Do x là số lượng khách thứ 51 trở lên nên x>0.
Cứ thêm 1 người thì giá còn (300000-5 000.1) đồng/người cho toàn bộ hành khách.
Thêm x người thì giá còn (300 000-5 000.x) đồng/người cho toàn bộ hành khách.
Doanh thu theo x: \(\left( {50 + x} \right).\left( {300000 - 5000x} \right)\) (VNĐ)
b) Do chi phí thực sự cho chuyến đi là 15 080 000 đồng nên để công ty không bị lỗ thì doanh thu phải lớn hơn hoặc bằng 15 080 000 đồng
Khi đó:
\(\begin{array}{l}\left( {50 + x} \right).\left( {300000 - 5000x} \right) \ge 15080000\\ \Leftrightarrow \left( {50 + x} \right).5000.\left( {60 - x} \right) \ge 15080000\\ \Leftrightarrow \left( {x + 50} \right)\left( {60 - x} \right) \ge 3016\\ \Leftrightarrow - {x^2} + 10x + 3000 \ge 3016\\ \Leftrightarrow - {x^2} + 10x - 16 \ge 0\\ \Leftrightarrow {x^2} - 10x + 16 \le 0\\ \Leftrightarrow \left( {x - 2} \right)\left( {x - 8} \right) \le 0\\ \Leftrightarrow 2 \le x \le 8\end{array}\)
Vậy số người của nhóm du khách nhiều nhất là 58 người.

a) Ta có x1 = 1 có tần số n1 = 2100 (lớn nhất)
⇒ Mốt của bảng phân bố đã cho là: Mo = 1
b) Trong sản xuất, nhà máy nên ưu tiên cho mẫu số 1