Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) Để có đc bảng này, người điều tra phải đi gặp lớp trưởng của từng lớp để lấy số liệu.
b) Dấu hiệu : Số học sinh nữ trong mỗi lớp
Các gt khác nhau của dấu hiệu và tần số của từng giá trị :
| x | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 24 | 25 | 28 |
| x | 2 | 1 | 3 | 3 | 3 | 1 | 4 | 1 | 1 | 1 |
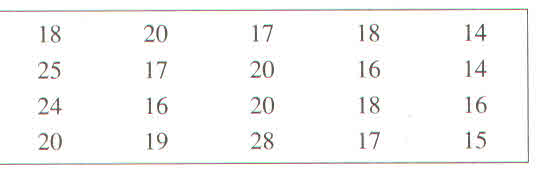
a) Để có được bảng này, người điều tra phải khảo sát số học sinh nữ của từng lớp trong trường THCS đó rồi thống kê.
b) Dấu hiệu ở đây là số lượng học sinh nữ của từng lớp trong 1 trường THCS.
Dãy giá trị khác nhau của dấu hiệu: \(14,15,16,17,18,19,20,24,25,28\)
Ta có bảng "tần số" các giá trị của dấu hiệu:
| \(x\) | \(14\) | \(15\) | \(16\) | \(17\) | \(18\) | \(19\) | \(20\) | \(24\) | \(25\) | \(28\) |
| \(n\) | \(2\) | \(1\) | \(3\) | \(3\) | \(3\) | \(1\) | \(4\) | \(1\) | \(1\) | \(1\) |

Gọi số học sinh lớp \(7A;7B;7C\) lần lượt là \(a;b;c\)
Theo đề bài ta có:
\(\dfrac{2}{3}a=\dfrac{3}{4}b=\dfrac{4}{5}c\Leftrightarrow\dfrac{2a}{3}=\dfrac{3b}{4}=\dfrac{4c}{5}\)
Tương đương với:
\(\dfrac{2a}{3}.\dfrac{1}{12}=\dfrac{3b}{4}.\dfrac{1}{12}=\dfrac{4c}{5}.\dfrac{1}{12}\)
\(\Leftrightarrow\dfrac{2a}{36}=\dfrac{3b}{48}=\dfrac{4c}{60}\)
\(\Leftrightarrow\dfrac{a}{18}=\dfrac{b}{16}=\dfrac{c}{15}\)
Áp dụng tính chất dãy tỉ số bằng nhau ta có:
\(\dfrac{a}{18}=\dfrac{b}{16}=\dfrac{c}{15}=\dfrac{a+b-c}{18+16-15}=\dfrac{57}{19}=3\)
\(\Rightarrow\left\{{}\begin{matrix}a=18.3=54\\b=16.3=48\\c=15.3=45\end{matrix}\right.\)

ĐỀ 2
I. PHẦN TRẮC NGHIỆM: (3 điểm)
Khoanh tròn chữ cái đứng trước câu trả lời đúng:
1. Trong các khẳng định sau, khẳng định sai là:
A. I ⊂ R
B. I ∪ Q = R
C. Q ⊂ I
D. Q ⊂ R
2. Kết quả của phép nhân (-0,5)3.(-0,5) bằng:
A. (-0,5)3
B. (-0,5)
C. (-0,5)2
D. (0,5)4
3. Giá trị của (-2/3) ³ bằng:

=> Chọn B
4. Nếu | x | = |-9 |thì:
A. x = 9 hoặc x = -9
B. x = 9
B. x = -9
D. Không có giá trị nào của x để thỏa mãn
5. Kết quả của phép tính 36.34. 32 bằng:
A. 2712
B. 312
C. 348
D. 2748
=> 39168
6. Kết quả của phép tính ![]()

Tần số tương ứng của các giá trị 7; 8; 9; 11 là 2; 2; 4; 1
Do đó, giá trị có tần số nhỏ nhất là 11
Chọn đáp án D

Câu 1 :
a, \(=\left(\dfrac{3}{4}.\dfrac{1}{5}\right).\left(26-44\right)=\dfrac{3}{20}.\left(-18\right)=\dfrac{-27}{10}\)b,
\(=\left(-8\right).\left(-0,75\right)-0,25.4-2.\dfrac{7}{6}\)
\(=\left(-6\right)-1-\dfrac{7}{3}=-7-2\dfrac{1}{3}=-9\dfrac{1}{3}\)
Câu 2 :
a, \(\rightarrow4\dfrac{1}{3}=\dfrac{6}{0,3}.\dfrac{x}{4}\)
\(\rightarrow\dfrac{13}{3}=20.\dfrac{x}{4}\)
\(\rightarrow13.4=20.x.4\rightarrow13=20.x\\ \Rightarrow x=\dfrac{13}{20}\)
b, \(\rightarrow\)TH1:
x + 1 = 4 , 5 \(\rightarrow x=4,5-1\Rightarrow x=3,5\)
\(\rightarrow\)TH2 :
x + 1 = 4 , 5 \(\rightarrow x=-4,5-1\Rightarrow x=-5,5\)
Câu 1.
a. \(\dfrac{3}{4}.26\dfrac{1}{5}-\dfrac{3}{4}.44\dfrac{1}{5}\)
\(=\dfrac{3}{4}.\left(26\dfrac{1}{5}-44\dfrac{1}{5}\right)\)
\(=\dfrac{3}{4}.(-18)\)
\(=-13\dfrac{1}{2}\)
b.\(\left(-2\right)^3.\left(-\dfrac{3}{4}\right)-0,25:\dfrac{1}{4}-2.1\dfrac{1}{6}\)
\(=\left(-8\right).\left(-\dfrac{3}{4}\right)-\dfrac{1}{4}:\dfrac{1}{4}-2.\dfrac{7}{6}\)
\(=6-1-\dfrac{7}{3}\)
\(=5-\dfrac{7}{3}\)
\(=\dfrac{8}{3}\)
Câu 2.
a. \(4\dfrac{1}{3}:\dfrac{x}{4}=6:0,3\)
\(4\dfrac{1}{3}:\dfrac{x}{4}=20\)
\(\dfrac{x}{4}=4\dfrac{1}{3}:20\)
\(\dfrac{x}{4}=\dfrac{13}{60}\)
\(\dfrac{15x}{60}=\dfrac{13}{60}\)
\(\Rightarrow15x=13\)
\(x=13:15\)
\(x=\dfrac{13}{15}\)
b. \(\left|x+1\right|=4,5\)
\(\Rightarrow x+1\in\left\{\pm4,5\right\}\)
* \(x+1=-4,5\)
\(x=-4,5-1\)
\(x=-5,5\)
* \(x+1=4,5\)
\(x=4,5-1\)
\(x=3,5\)
Vậy \(x\in\left\{-5,5;3,5\right\}\)

Bài 1:
a: \(\dfrac{45^{10}\cdot5^{20}}{75^{15}}=\dfrac{5^{10}\cdot3^{20}\cdot5^{20}}{\left(5^2\right)^{15}\cdot3^{15}}=3^5\)
b: \(\dfrac{2^{15}\cdot9^4}{6^6\cdot8^3}=\dfrac{2^{15}\cdot3^8}{2^6\cdot2^9\cdot3^6}=3^2\)

Dài ngoằng nhìn phát ngán
a)\(\left(x^4\right)^{^3}=\frac{x^{18}}{x^7}\Leftrightarrow x^{12}=x^{18-7}\Leftrightarrow x^{12}=x^{11}\Rightarrow\orbr{\begin{cases}x=0\\x=1\end{cases}}\)
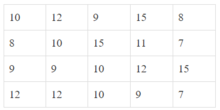

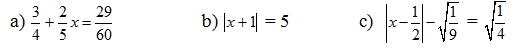
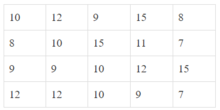
Tần số tương ứng của các giá trị 9, 10, 15 là 4, 4, 3
Chọn đáp án A.