Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) Để có đc bảng này, người điều tra phải đi gặp lớp trưởng của từng lớp để lấy số liệu.
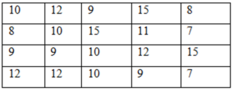
b) Dấu hiệu : Số học sinh nữ trong mỗi lớp
Các gt khác nhau của dấu hiệu và tần số của từng giá trị :
| x | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 24 | 25 | 28 |
| x | 2 | 1 | 3 | 3 | 3 | 1 | 4 | 1 | 1 | 1 |
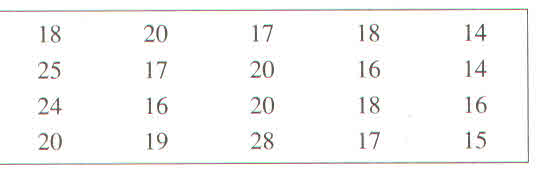
a) Để có được bảng này, người điều tra phải khảo sát số học sinh nữ của từng lớp trong trường THCS đó rồi thống kê.
b) Dấu hiệu ở đây là số lượng học sinh nữ của từng lớp trong 1 trường THCS.
Dãy giá trị khác nhau của dấu hiệu: \(14,15,16,17,18,19,20,24,25,28\)
Ta có bảng "tần số" các giá trị của dấu hiệu:
| \(x\) | \(14\) | \(15\) | \(16\) | \(17\) | \(18\) | \(19\) | \(20\) | \(24\) | \(25\) | \(28\) |
| \(n\) | \(2\) | \(1\) | \(3\) | \(3\) | \(3\) | \(1\) | \(4\) | \(1\) | \(1\) | \(1\) |

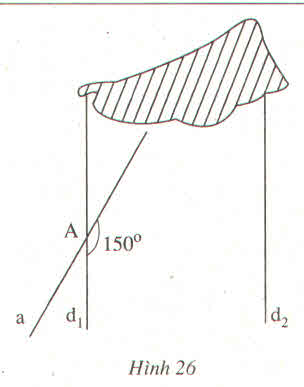
Ta có : ˆA1A1^ và ˆA2A2^ là hai góc kề bù nên:
ˆA1+ˆA2=1800⇒ˆA2=1800−ˆA1=1800−1500=300A1^+A2^=1800⇒A2^=1800−A1^=1800−1500=300
Vì d1 // d2 và ˆA2A2^ so le trong với ˆB1B1^
⇒ˆB1=ˆA2=300⇒B1^=A2^=300
Vậy ˆB1=300
Gọi B giao điểm của a và d2.
d1 // d2 nên góc nhọn tại B bằng góc nhọn tại A và bằng
1800 - 1500= 300.

Có 7 giá trị khác nhau của dấu hiệu, đó là: 15;16;17;18;20;22;24.
Đáp án cần chọn là: A

Có 7 giá trị khác nhau của dấu hiệu là 7,8,9,10,11,12,15.
Đáp án cần chọn là: B

bạn ơi bạn đã học cái tính chất trong 1 tam giác cân thì trung tuyến vừa là đường cao và là đường trung trực chưa

cũng đúng bn ạ, nhưng dài hơn cái trên, mik = tuổi bn. kb nha
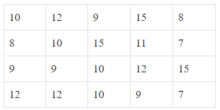

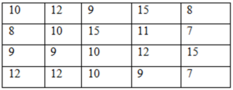

Có 20 giá trị của dấu hiệu
Đáp án cần chọn là: A