

Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



Chọn D
Chọn 3 học sinh (có thứ tự) xếp vào 10 vị trí có số cách chọn là số chỉnh hợp chập 3 của 10 phần tử: A 10 3

Chọn D
Nhóm có tất cả 9 học sinh nên số cách xếp 9 học sinh này ngồi vào một hàng có 9 ghế là 9! = 362880(cách).
Vậy số phần tử không gian mẫu là n ( Ω ) = 362880
Đặt biến cố A: “ 3 học sinh lớp không ngồi ghế liền nhau”.
Giả sử học sinh lớp 10 ngồi 3 ghế liền nhau. Ta xem 3 học sinh này là một nhóm
+/ Xếp X và 6 bạn còn lại vào ghế có 7! cách xếp.
+/ Ứng với mỗi cách xếp ở trên, có 3! cách xếp các bạn trong nhóm X.
Vậy theo quy tắc nhân ta có số cách xếp là: 7!.3! = 30240 (cách).
Suy ra số cách xếp để học sinh lớp không ngồi cạnh nhau là (cách) .
Vậy xác suất để học sinh lớp 10 không ngồi cạnh nhau là 362880 - 30240 = 332640 (cách)
=> n(A) = 332640
Vậy xác suất để học sinh lớp 10 không ngồi cạnh nhau là
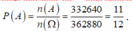

Chọn A.
Số phần tử của không gian mẫu là n(W =) 6!.
Gọi A là biến cố : "Các bạn học sinh nam ngồi đối diện các bạn nữ".
Chọn chỗ cho học sinh nam thứ nhất có 6 cách.
Chọn chỗ cho học sinh nam thứ 2 có 4 cách (không ngồi đối diện học sinh nam thứ nhất)
Chọn chỗ cho học sinh nam thứ 3 có 2 cách (không ngồi đối diện học sinh nam thứ nhất, thứ hai).
Xếp chỗ cho 3 học sinh nữ : 3! cách.
Theo quy tắc nhân ta có cách
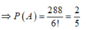

Chọn D
Cách 1. Xếp ngẫu nhiên 10 học sinh vào hai dãy ghế có cách.
Đánh số ghế lần lượt từ 1 đến 10.
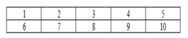
Xếp học sinh thỏa mãn bài toán xảy ra hai khả năng sau:
Khả năng 1: Nam ngồi vị trí lẻ, nữ ngồi vị trí chẵn có 5!.5! cách.
Khả năng 2: Nam ngồi vị trí chẵn, nữ ngồi vị trí lẻ có 5!.5! cách.
Vậy có tất cả 2. ( 5 ! ) 2 cách.
Xác suất cần tìm bằng 
Cách 2: Xếp ngẫu nhiên 10 học sinh vào hai dãy ghế, có 10! cách xếp.
Ta chia hai dãy ghế thành 5 cặp ghế đối diện:
+ Chọn 1 nam và 1 nữ xếp vào cặp ghế 1 có ![]() cách;
cách;
+ Chọn 1 nam và 1 nữ xếp vào cặp ghế 2 có ![]() cách;
cách;
+ Chọn 1 nam và 1 nữ xếp vào cặp ghế 3 có ![]() cách;
cách;
+ Chọn 1 nam và 1 nữ xếp vào cặp ghế 4 có ![]() cách;
cách;
+ Chọn 1 nam và 1 nữ xếp vào cặp ghế 5 có 1 cách.
Vậy có tất cả ![]() cách xếp thỏa mãn.
cách xếp thỏa mãn.
Xác suất cần tìm bằng 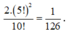

Chọn A
Số cách xếp ngẫu nhiên 6 học sinh vào dãy ghế: n ( Ω ) = 6!.
Gọi M là biến cố “xếp 6 học sinh vào dãy ghế mà không có học sinh lớp C nào ngồi cạnh nhau”.
Gọi M ¯ là biến cố “xếp 6 học sinh vào dãy ghế mà hai học sinh lớp C ngồi cạnh nhau”.
Ghép 2 học sinh lớp C thành nhóm X.
Xếp nhómX, 2 học sinh lớp A, 2 học sinh lớp B vào dãy ghế: 5!.
Hoán đổi vị trí 2 học sinh lớp C: 2!.
![]()
Vậy ![]()