K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
26 tháng 8 2021
1, \(sin\left(x+\dfrac{\pi}{6}\right)+cos\left(x+\dfrac{\pi}{6}\right)=\dfrac{\sqrt{6}}{2}\)
⇔ \(\dfrac{\sqrt{2}}{2}sin\left(x+\dfrac{\pi}{6}\right)+\dfrac{\sqrt{2}}{2}cos\left(x+\dfrac{\pi}{6}\right)=\dfrac{\sqrt{3}}{2}\)
⇔ \(sin\left(x+\dfrac{\pi}{6}+\dfrac{\pi}{4}\right)=sin\dfrac{\pi}{4}\)
2, \(\left(\sqrt{3}-1\right)sinx+\left(\sqrt{3}+1\right)cosx=1-\sqrt{3}\)
⇔ \(\dfrac{\left(\sqrt{3}-1\right)}{2\sqrt{2}}sinx+\dfrac{\left(\sqrt{3}+1\right)}{2\sqrt{2}}cosx=\dfrac{1-\sqrt{3}}{2\sqrt{2}}\)
⇔ sinx . si
HA
3
AH
Akai Haruma
Giáo viên
2 tháng 9 2023
a.
Tìm min:
$y=(4\sin ^2x-4\sin x+1)+2=(2\sin x-1)^2+2$
Vì $(2\sin x-1)^2\geq 0$ với mọi $x$ nên $y=(2\sin x-1)^2+2\geq 0+2=2$
Vậy $y_{\min}=2$
----------------
Mặt khác:
$y=4\sin x(\sin x+1)-8(\sin x+1)+11$
$=(\sin x+1)(4\sin x-8)+11$
$=4(\sin x+1)(\sin x-2)+11$
Vì $\sin x\in [-1;1]\Rightarrow \sin x+1\geq 0; \sin x-2<0$
$\Rightarrow 4(\sin x+1)(\sin x-2)\leq 0$
$\Rightarrow y=4(\sin x+1)(\sin x-2)+11\leq 11$
Vậy $y_{\max}=11$
AH
Akai Haruma
Giáo viên
2 tháng 9 2023
b.
$y=\cos ^2x+2\sin x+2=1-\sin ^2x+2\sin x+2$
$=3-\sin ^2x+2\sin x$
$=4-(\sin ^2x-2\sin x+1)=4-(\sin x-1)^2\leq 4-0=4$
Vậy $y_{\max}=4$.
---------------------------
Mặt khác:
$y=3-\sin ^2x+2\sin x = (1-\sin ^2x)+(2+2\sin x)$
$=(1-\sin x)(1+\sin x)+2(1+\sin x)=(1+\sin x)(1-\sin x+2)$
$=(1+\sin x)(3-\sin x)$
Vì $\sin x\in [-1;1]$ nên $1+\sin x\geq 0; 3-\sin x>0$
$\Rightarrow y=(1+\sin x)(3-\sin x)\geq 0$
Vậy $y_{\min}=0$
MH
9 tháng 4 2017
a) Dễ thấy cosx = 0 không thỏa mãn phương trình đã cho nên chiaw phương trình cho cos2x ta được phương trình tương đương 2tan2x + tanx - 3 = 0.
Đặt t = tanx thì phương trình này trở thành
2t2 + t - 3 = 0 ⇔ t ∈ {1 ; 
}.
Vậy 
b) Thay 2 = 2(sin2x + cos2x), phương trình đã cho trở thành
3sin2x - 4sinxcosx + 5cos2x = 2sin2x + 2cos2x
⇔ sin2x - 4sinxcosx + 3cos2x = 0
⇔ tan2x - 4tanx + 3 = 0
⇔ 
⇔ x = 
+ kπ ; x = arctan3 + kπ, k ∈ Z.
c) Thay sin2x = 2sinxcosx ; 
= (sin2x + cos2x) vào phương trình đã cho và rút gọn ta được phương trình tương đương
sin2x + 2sinxcosx - 
cos2x = 0 ⇔ tan2x + 4tanx - 5 = 0 ⇔ 
⇔ x = + kπ ; x = arctan(-5) + kπ, k ∈ Z.
d) 2cos2x - 3√3sin2x - 4sin2x = -4
⇔ 2cos2x - 3√3sin2x + 4 - 4sin2x = 0
⇔ 6cos2x - 6√3sinxcosx = 0 ⇔ cosx(cosx - √3sinx) = 0
⇔ 
NV
Nguyễn Việt Lâm
Giáo viên
12 tháng 7 2021
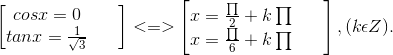
a.
\(\left(sin^2\dfrac{x}{2}+cos^2\dfrac{x}{2}\right)^2-2sin^2\dfrac{x}{2}cos^2\dfrac{x}{2}=\dfrac{1}{2}\)
\(\Leftrightarrow2-\left(2sin\dfrac{x}{2}cos\dfrac{x}{2}\right)^2=1\)
\(\Leftrightarrow1-sin^2x=0\)
\(\Leftrightarrow cos^2x=0\)
\(\Leftrightarrow x=\dfrac{\pi}{2}+k\pi\)
NV
Nguyễn Việt Lâm
Giáo viên
12 tháng 7 2021
b.
\(\left(sin^2x+cos^2x\right)^3-3sin^2x.cos^2x\left(sin^2x+cos^2x\right)=\dfrac{7}{16}\)
\(\Leftrightarrow1-\dfrac{3}{4}\left(2sinx.cosx\right)^2=\dfrac{7}{16}\)
\(\Leftrightarrow16-12.sin^22x=7\)
\(\Leftrightarrow3-4sin^22x=0\)
\(\Leftrightarrow3-2\left(1-cos4x\right)=0\)
\(\Leftrightarrow cos4x=-\dfrac{1}{2}\)
\(\Leftrightarrow4x=\pm\dfrac{2\pi}{3}+k2\pi\)
\(\Leftrightarrow x=\pm\dfrac{\pi}{6}+\dfrac{k\pi}{2}\)
NV
Nguyễn Việt Lâm
Giáo viên
4 tháng 10 2020
1.
\(\Leftrightarrow3x=k\pi\Leftrightarrow x=\frac{k\pi}{3}\)
2.
\(\Leftrightarrow cos5x=0\Leftrightarrow5x=\frac{\pi}{2}+k\pi\Leftrightarrow x=\frac{\pi}{10}+\frac{k\pi}{5}\)
4.
\(cos3x+cosx+cos2x=0\)
\(\Leftrightarrow2cos2x.cosx+cos2x=0\)
\(\Leftrightarrow cos2x\left(2cosx+1\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}cos2x=0\\cosx=-\frac{1}{2}\end{matrix}\right.\) \(\Leftrightarrow\left[{}\begin{matrix}x=\frac{\pi}{4}+\frac{k\pi}{2}\\x=\pm\frac{2\pi}{3}+k2\pi\end{matrix}\right.\)
NV
Nguyễn Việt Lâm
Giáo viên
4 tháng 10 2020
5.
\(sin6x+sin2x+sin4x=0\)
\(\Leftrightarrow2sin4x.cos2x+sin4x=0\)
\(\Leftrightarrow sin4x\left(2cos2x+1\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}sin4x=0\\cos2x=-\frac{1}{2}\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=\frac{k\pi}{4}\\x=\pm\frac{\pi}{3}+k\pi\end{matrix}\right.\)
6. ĐKXĐ; ...
\(\Leftrightarrow tanx+tan2x=1-tanx.tan2x\)
\(\Leftrightarrow\frac{tanx+tan2x}{1-tanx.tan2x}=1\)
\(\Leftrightarrow tan3x=1\)
\(\Leftrightarrow x=\frac{\pi}{12}+\frac{k\pi}{3}\)
1 tháng 8 2023
a: tan x(cot^2x-1)
\(=\dfrac{1}{cotx}\left(cot^2x-cotx\cdot tanx\right)\)
=cotx-tanx/cotx=cotx(1-tan^2x)
b: \(tan^2x-sin^2x=\dfrac{sin^2x}{cos^2x}-sin^2x\)
\(=sin^2x\left(\dfrac{1}{cos^2x}-1\right)=sin^2x\cdot\dfrac{sin^2x}{cos^2x}=sin^2x\cdot tan^2x\)
c: \(\dfrac{cos^2x-sin^2x}{cot^2x-tan^2x}=\dfrac{cos^2x-sin^2x}{\dfrac{cos^2x}{sin^2x}-\dfrac{sin^2x}{cos^2x}}\)
\(=\left(cos^2x-sin^2x\right):\dfrac{cos^4x-sin^4x}{sin^2x\cdot cos^2x}\)
\(=\dfrac{sin^2x\cdot cos^2x}{1}=sin^2x\cdot cos^2x\)
=>sin^2x*cos^2x-cos^2x=cos^2x(sin^2x-1)
=-cos^2x*cos^2x=-cos^4x
=>ĐPCM
20 tháng 8 2023
a: ĐKXĐ: \(x\in R\)
=>TXĐ: D=R
b; ĐKXĐ: 2x-4>=0
=>x>=2
TXĐ: D=[2;+\(\infty\))
c: ĐKXĐ: 1-cos^2x>=0
=>sin^2x>=0(luôn đúng)
bấm máy
máy có cu giải đc