Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

- Vì A≠G mà chữ số hàng chục của tổng là 0 nên phép cộng có nhớ 1 sang hàng trăm nên ở hàng trăm: H + N + 1 (nhớ) = 10; nhớ 1 sang hàng nghìn. Do đó H + N = 10 - 1 = 9.
- Phép cộng ở hàng nghìn: N + 1 (nhớ) = 2 nên N = 2 - 1 = 1.
Thay N = 1 ta có: H + 1 = 9 nên H = 9 - 1 = 8
- Phép cộng ở hàng đơn vị: Có 2 trường hợp xảy ra:
* Trường hợp 1: Phép cộng ở hàng đơn vị không nhớ sang hàng chục.
Khi đó: M + O = 0 và A + G = 10.
Ta có bảng: (Lưu ý 4 chữ M, O, A, G phải khác nhau và khác 1; 8)
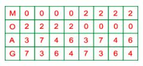
* Trường hợp 2: Phép cộng ở hàng đơn vị có nhớ 1 sang hàng chục.
Khi đó: M + O = 12 và A + G = 9. Ta có bảng:
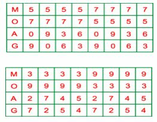
Vậy bài toán có 24 đáp số như trên.

BENJAMIN có 8 chữ cái
2; 3; 4; 5; 6; 7; 8 là 7 số
:VVV??????

a, \(\overline{ab,b}\) - \(\overline{c,c}\) = \(\overline{0,a}\)
(\(\overline{ab,b}\) - \(\overline{c,c}\)) \(\times\)10 = \(\overline{0,a}\)
\(\overline{abb}\) - \(cc\) = \(a\)
\(a\times\)100 + \(b\)\(\times\)11 - \(c\times\)11 = \(a\)
\(a\times\)100 + \(b\times\)11 - \(c\times\)11 - \(a\) = 0
\(a\times\)99 + \(b\) \(\times\)11 - \(c\times\) 11 = 0
11\(\times\)(\(a\times\)9 + \(b\) - \(c\)) = 0
\(a\times\) 9 + \(b\) - \(c\) = 0
\(a\times\) 9 = \(c-b\) ⇒ \(c-b\)⋮9 ⇒ \(c\) = \(b\) ; \(c\) - \(b\) = 9;
th: \(c\) = \(b\) ⇒ \(a\times\)9 = 0 ⇒ \(a\) = 0 (loại)
th: \(c-b=9\) ⇒ \(c=9+b\) ⇒ \(b\) = 0; \(c\) = 9
\(a\times\) 9 = 9 - 0 = 9 ⇒ \(a\) = 1
Vậy thay \(a=1;b=0;c=9\) vào biểu thức: \(\overline{ab,b}-\overline{c,c}=\overline{o,a}\) ta được:
10,0 -9,9 = 0,1
b, \(\overline{b,a}\) - \(\overline{a,b}\) = 2,7
(\(\overline{b,a}\) - \(\overline{a,b}\))\(\times\)10 = 2,7 \(\times\) 10
\(\overline{ba}\) - \(\overline{ab}\) = 27
\(b\times10+a-a\times10-b\) = 27
(\(b\times10\) - \(b\)) - (\(a\) \(\times\) 10 - \(a\)) = 27
(\(b\times10-b\times1\)) - (\(a\times\)10 - \(a\)\(\times\)1) = 27
\(b\)\(\times\)(10 -1) - \(a\) \(\times\)( 10 - 1) =27
\(b\times\) 9 - \(a\times9\) = 27
9\(\times\) (\(b-a\)) = 27
\(b-a\) = 27 : 9
\(b-a\) = 3 ⇒ \(b\) = 3 + \(a\) ≤ 9 ⇒ \(a\) ≤ 9 - 3 = 6
Lập bảng ta có:
| \(a\) | 0 | 1 | 2 | 3 | 4 | 5 | 6 |
| \(b\) = \(a+3\) | 3 | 4 | 5 | 6 | 7 | 8 |
9 |
Thay các giá trị của \(a;b\) lần lượt vào biểu thức \(\overline{b,a}-\overline{a,b}\) = 2,7 ta có:
3,0 - 0,3 = 2,7
4,1 - 1,4 = 2,7
5,2 - 2,5 = 2.7
6,3 - 3,6 = 2,7
8,5 - 5,8 = 2,7
9,6 - 6,9 = 2,7

Ta có CCCCCCCCC = C .111111111 = 12345679 . C . 9
Ta tìm cách phân tích số CCCCCCCCC thành tích của hai số ABCDEFGH (Số có 8 chữ số) và AK (Số có 2 chữ số).
Xét lần lượt C = 1 ; 2; ...; 9 như sau:
- Với C = 1: Ta có CCCCCCCCC = = 111111111 = 12345679 . 9 là cách phân tích duy nhất thành một số có 8 chữ số với số có 1 chữ số. Vậy không thỏa mãn.
- Với C = 2: Ta có CCCCCCCCC = 222222222 = 12345679 . 2 . 9 = 12345679 . 18 là cách phân tích duy nhất thành một số có 8 chữ số với số có 2 chữ số. Tuy nhiên không phải dạng ABCDEFGH x AK = CCCCCCCCC (vì C trong ABCDEFGH bằng 3 trong khi C trong CCCCCCCCC lại bằng 2)
- Với C = 3: Ta có CCCCCCCCC = 333333333 = 12345679 . 3 . 9 = 12345679 . 27 là cách phân tích duy nhất thành một số có 8 chữ số với số có 2 chữ số. Tuy nhiên không phải dạng ABCDEFGH x AK = CCCCCCCCC (vì A trong ABCDEFGH bằng 1 trong khi A trong AK lại bằng 2)
- Với C = 4: Ta có CCCCCCCCC = 444444444 = 12345679 . 4 . 9 = 12345679 . 36 = 24691358 x 18. Có hai cách phân tích duy số 444444444 là 12345679 x 36 và 24691358 x 18, cả hai cách đều không thỏa mãn dạng ABCDEFGH x AK = CCCCCCCCC
Cứ xét tiếp tục ta sẽ thấy với C = 6 thì:
666666666 = 12345679 x 6 x 9 = 12345679 x 54 = 24691358 x 27 = 37037037 x 18
Có 3 cách biểu diễn số 666666666 thành tích của số có 8 chữ số và số có 2 chữ số. Chỉ có duy nhất cách 666666666 = 24691358 x 27 là thỏa mãn dạng CCCCCCCCC = ABCDEFGH x AK.
Vậy phép nhân thỏa mãn điều kiện bài toán là: 24691358 x 27 = 666666666.
Xác định lại đề
"Mỗi chữ cái khác nhau tương ứng với mỗi số khác nhau"
Theo mình
"Mỗi chữ cái khác nhau tương ứng với mỗi chữ số khác nhau"
Cái đấy thì ai cũng biết