Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Do các tấm thẻ giống nhau, nên lấy 3 tấm từ 10 tấm không quan tâm thứ tự có \(C_{10}^3 = 120\)cách, suy ra \(n\left( \Omega \right) = 120\)
Gọi A là biến cố “Tích các số ghi trên ba thẻ đó là số chẵn”
Để tích các số trên thẻ là số chẵn thì ít nhất có 1 thẻ là số chẵn
Để chọn ra 3 thẻ thuận lợi cho biến cố A ta có 3 khả năng
+) Khả năng 1: 3 thẻ chọn ra có 1 thẻ có số chẵn và 2 thẻ có số lẻ có \(5.C_5^2 = 50\) khả năng
+) Khả năng 2: 3 thẻ chọn ra có 2 thẻ có số chẵn và 1 thẻ có số lẻ có \(C_5^2.5 = 50\) khả năng
+) Khả năng 3: 3 thẻ chọn ra có đều là có số chắn có \(C_5^3 = 10\) khả năng
Suy ra \(n\left( A \right) = 50 + 50 + 10 = 110\)
Vậy xác suất của biến cố A là: \(P(A) = \frac{{110}}{{120}} = \frac{{11}}{{12}}\)

a) Kí hiệu \({X_1},{X_2},...,{X_7}\) là bảy thẻ màu xanh, \({D_1},{D_2},...,{D_5}\) là 5 thẻ màu đỏ và \({V_1},{V_2}\) là hai thẻ màu vàng.
Ta có không gian mẫu là \(\Omega = \left\{ {{X_1},{X_2},...,{X_7},{D_1},{D_2},...,{D_5},{V_1},{V_2}} \right\}\).
b) Ta có \(A = \left\{ {{D_1},{D_2},{D_3},{D_4},{D_5},{V_1},{V_2}} \right\},B = \left\{ {{X_2},{X_3},{D_2},{D_3},{V_2}} \right\}\).

TH1: tấm chia hết cho 5 là số lẻ
=>Có \(5\cdot C^3_{24}\cdot C^4_{25}\left(cách\right)\)
TH2: tấm chia hết cho 5 là sốchẵn
=>Có \(5\cdot C^3_4\cdot C^4_{25}\left(cách\right)\)
=>n(A)=506000
n(omega)=\(C^8_{50}=536878650\)
=>P=40/42441

Ta có \(n\left( \Omega \right) = C_{11}^2 = 55\).
a) Có 5 số lẻ là \(\left\{ {11;13;15;17;19} \right\}\) nên \(n\left( C \right) = C_5^2 = 10\). Vậy \(P\left( C \right) = \frac{{10}}{{55}} = \frac{2}{{11}}\).
b) Có 6 số chẵn là \(\left\{ {10;12;14;16;18;20} \right\}\) nên \(n\left( D \right) = C_6^2 = 15\). Vậy \(P\left( D \right) = \frac{{15}}{{55}} = \frac{3}{{11}}\).

Số phần tử của không gian mẫu là\(n\left( \Omega \right) = 30\).
Gọi E là biến cố: “Số trên thẻ được rút ra là số chia hết cho 5”
Ta có \(E = \left\{ {5;10;15;20;25;30} \right\} \Rightarrow n\left( E \right) = 6\)
Vậy xác suất của biến cố E là \(P\left( E \right) = \frac{{n\left( E \right)}}{{n\left( \Omega \right)}} = \frac{1}{5}\).
Chọn B

Không gian mẫu: \(A_6^3=120\)
Gọi số cần lập có dạng \(\overline{abc}\)
Số chia hết cho 5 \(\Rightarrow c=5\) (1 cách chọn)
Chọn và hoán vị cặp ab: \(A_5^2=20\) cách
\(\Rightarrow1.20=20\) số chia hết cho 5
Xác suất: \(P=\dfrac{20}{120}=\dfrac{1}{6}\)

a) Mỗi phần tử của không gian mẫu là một tổ hợp chập 2 của 20 phần tử. Do đó, số phần tử của không gian mẫu là: \(n\left( \Omega \right) = C_{20}^2\) ( phần tử)
b) Gọi A là biến cố “Tích các số trên hai thẻ là số lẻ”
Để tích các số trên thẻ là số lẻ thì cả hai thẻ bốc được đểu phải là số lẻ vậy nên ta phải chọn ngẫu nhiên 2 thẻ từ 10 thẻ số lẻ. Do đó, số phần tử các kết quả thuận lợi cho biến cố A là tổ hợp chập 2 của 10 phần tử: \(n\left( A \right) = C_{10}^2\) ( phần tử)
Vậy xác suất của biến cố A là: \(P\left( A \right) = \frac{{n\left( A \right)}}{{n\left( \Omega \right)}} = \frac{{C_{10}^2}}{{C_{20}^2}} = \frac{9}{{38}}\)

Gọi B là tổng các chữ số của A. Ta có A = 123456...9899100
Lúc này ta cần tính B = 1 + 2 + ... + 8 + 9 + 1 +0 +1 + 1 + ... + 9 + 9 + 1 + 0 + 0
Ta sẽ tính sác xuất xuất hiện ( tức tần số suất hiện ) của các chữ số 0 ; 1 ; 2 ; ... ; 8 ; 9
Ta sẽ thấy 0 xuất hiện 11 lần ; 1 xuất hiện 21 lần còn các chữ số còn lại là 2 ; 3 ;... ;9 thì xuất hiện 20 lần
Vậy B = 0 x 1 + 1 x 21 + ( 2 + 3 + ... + 9 ) x 20 = 901 ko chia hết cho 9 nên ko thể chia hết cho 2007

Gọi \(S=\left\{\overline{abc}\right\}\)
a có 5 cách chọn
b có 5 cách chọn
c có 4 cách chọn
=>S có 5*5*4=100 số
Gọi \(\overline{abc}\) là số chia hết cho 5
TH1: c=5
=>a có 4 cách và b có 4 cách
=>Có 16 cách
TH2: c=0
=>a có 5 cách và b có 4 cách
=>Có 5+4=20 cách
=>Có 16+20=36(cách)
\(n\left(\Omega\right)=C^2_{100}\)
\(n\left(B\right)=C^2_{36}\)
=>\(P\left(B\right)=\dfrac{7}{55}\)
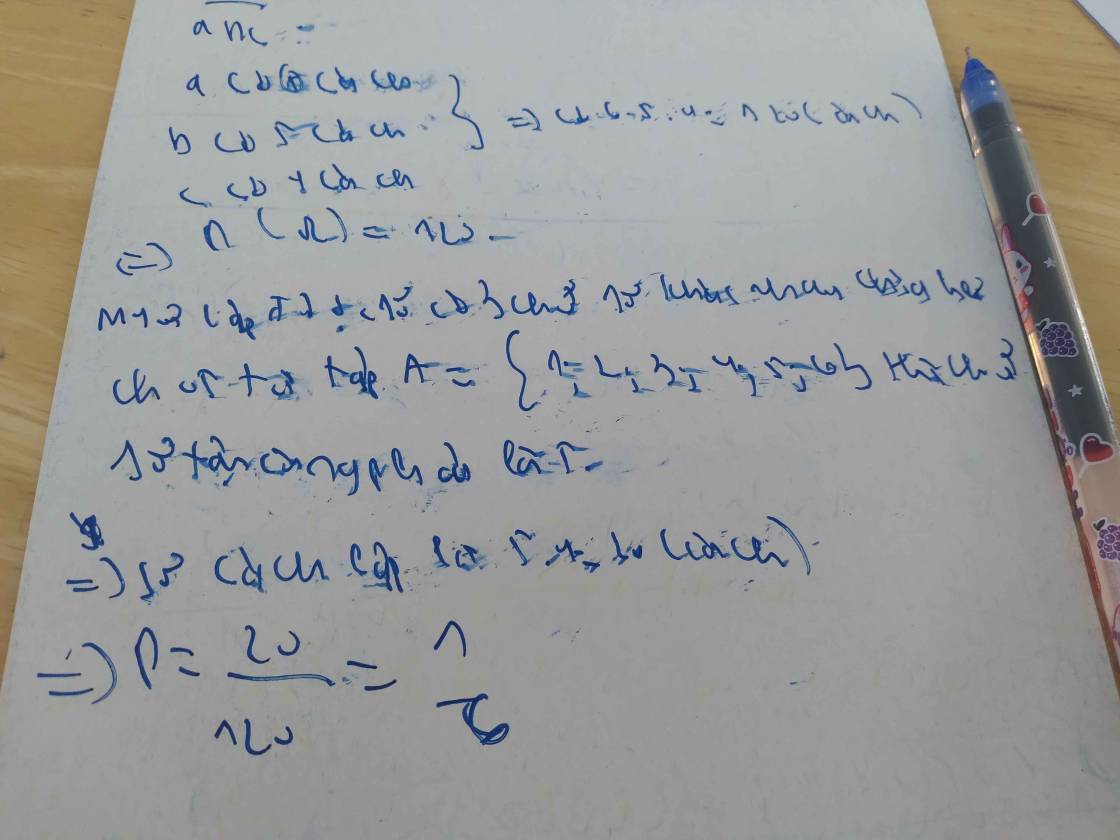
Gọi số lập được có dạng \(\overline {{a_1}{a_2}{a_3}{a_4}{a_5}} \) với \(\left( {{a_1},{a_2},{a_3},{a_4},{a_5}} \right) = 1,2,3,4,5\)
Tổng số khả năng xảy ra của phép thử là \(n\left( \Omega \right) = 5!\)
a) Biến cố “a là số chẵn” xảy ra khi chữ số tận cùng là số chẵn, suy ra \({a_5} = \left\{ {2,4} \right\}\)
Số kết quả thuận lợi cho biến cố “a là số chẵn” là \(n = 4!.2\)
Vậy xác suất của biến cố “a là số chẵn” là \(P = \frac{{4!.2}}{{5!}} = \frac{2}{5}\)
b) Biến cố “a chia hết cho 5” xảy ra khi chữ số tận cùng là số 5
Suy ra, số kết quả thuận lợi cho biến cố “a chia hết cho 5” là \(n = 4!.1\)
Vậy xác suất của biến cố “a là số chẵn” là \(P = \frac{{4!.1}}{{5!}} = \frac{1}{5}\)
c) Biến cố “\(a \ge 32000\)” xảy ra khi a có dạng như dưới đây\(\overline {5{a_2}{a_3}{a_4}{a_5}} ;\overline {4{a_2}{a_3}{a_4}{a_5}} ;\overline {34{a_3}{a_4}{a_5}} ;\overline {35{a_3}{a_4}{a_5}} ;\overline {32{a_3}{a_4}{a_5}} \)
Suy ra, số kết quả thuận lợi cho biến cố “\(a \ge 32000\)” là \(n = 2.4! + 3.3!\)
Vậy xác suất của biến cố “\(a \ge 32000\)” là \(P = \frac{{2.4! + 3.3!}}{{5!}} = \frac{{11}}{{20}}\)
d) Để sắp xếp các chữ số của a ta cần thực hiện hai công đoạn
Công đoạn 1: Sắp xếp 2 chữ số chẵn trước có \(2!\) cách
Công đoạn 2: Sắp xếp 3 chũ số lẻ xen vào 3 chỗ trồng tạo bởi 2 chữ số chẵn có \(3!\) cách
Suy ra, số kết quả thuận lợi cho biến cố “Trong các chữ số của a không có hai chữ số lẻ nào đứng cạnh nhau” là \(2!.3!\)
Vậy xác suất của biến cố là \(P = \frac{{2!.3!}}{{5!}} = \frac{1}{{10}}\)