Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Gọi A là biến cố "Rút được 2 lá bài cơ".
Số kết quả thuận lợi là \(\left|\Omega_A\right|=C^2_{13}=78\).
Số kết quả có thể xảy ra là \(\left|\Omega\right|=C^2_{52}=1326\).
\(\Rightarrow\) Xác suất xảy ra biến cố A là \(P\left(A\right)=\dfrac{78}{1326}=\dfrac{1}{17}\).

Số phần tử không gian mẫu: n(Ω)=52
Số phần tử của biến cố xuất hiện lá J đỏ hay lá 5 là n(A)=2+4=6
Suy ra 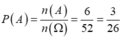
Chọn B.

Không gian mẫu: \(C_{52}^2\)
Số cách rút không có quân K nào: \(C_{48}^2\)
Xác suất: \(P=\dfrac{C_{52}^2-C_{48}^2}{C_{52}^2}=...\)

Lời giải:
Rút 5 trong 52 lá bài, có $C^5_{52}$ kết quả.
Rút 5 lá 10, J, Q, K, A đồng chất, có 4 kết quả (bích, tép, cơ, rô)
Xác suất rút được 5 lá thỏa mãn đề: $\frac{4}{C^5_{52}}$

Số phần tử không gian mẫu: n(Ω) = 52
Số phần tử của biến cố xuất hiện lá bích n(A) = 13
Suy ra 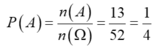
Chọn B.

Số phần tử không gian mẫu: n(Ω) = 52
Số phần tử của biến cố xuất hiện lá át hay lá rô n(A) = 4 +12 = 16.
Suy ra 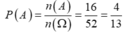
Chọn C.

Số phần tử không gian mẫu: n(Ω)=52
Số phần tử của biến cố xuất hiện lá át n(A)=4
Suy ra 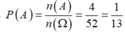
Chọn C.

Đáp án C.
Số cách chọn ngẫu nhiên 2 lá phiếu là: C 9 2 = 36 (cách)
Các cặp số có tổng là một số lẻ lớn hơn hoặc bằng 15 là: (9;8); (9;6); (8;7). Xác suất để tổng của hai số ghi trên hai lá phiếu rút được là một số lẻ lớn hơn hoặc bằng 15 là: 3 36 = 1 12

Đáp án C
Số cách rút hai lá phiếu là C 9 2
Gọi p là biến cố hai lá phiếu rút được có tổng lẻ lớn hơn hoặc bằng 15
![]()
![]()
Gọi \(A\) là biến cố “Hạt giống thứ nhất nảy mầm”, \(B\) là biến cố “Hạt giống thứ hai nảy mầm”.
\(P\left( A \right) = P\left( B \right) = 0,8 \Rightarrow P\left( {\bar A} \right) = P\left( {\bar B} \right) = 1 - 0,8 = 0,2\)
Xác suất để có đúng 1 trong 2 hạt giống đó nảy mầm là:
\(P\left( {A\bar B} \right) + P\left( {\bar AB} \right) = P\left( A \right).P\left( {\bar B} \right) + P\left( {\bar A} \right).P\left( B \right) = 0,8.0,2 + 0,2.0,8 = 0,32\)