Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
a) Ta có: \(A=\dfrac{a^2-1}{3}\cdot\sqrt{\dfrac{9}{\left(1-a\right)^2}}\)
\(=\dfrac{\left(a+1\right)\cdot\left(a-1\right)}{3}\cdot\dfrac{3}{\left|1-a\right|}\)
\(=\dfrac{\left(a+1\right)\left(a-1\right)}{1-a}\)
=-a-1
b) Ta có: \(B=\sqrt{\left(3a-5\right)^2}-2a+4\)
\(=\left|3a-5\right|-2a+4\)
\(=5-3a-2a+4\)
=9-5a
c) Ta có: \(C=4a-3-\sqrt{\left(2a-1\right)^2}\)
\(=4a-3-\left|2a-1\right|\)
\(=4a-3-2a+1\)
\(=2a-2\)
d) Ta có: \(D=\dfrac{a-2}{4}\cdot\sqrt{\dfrac{16a^4}{\left(a-2\right)^2}}\)
\(=\dfrac{a-2}{4}\cdot\dfrac{4a^2}{\left|a-2\right|}\)
\(=\dfrac{a^2\left(a-2\right)}{-\left(a-2\right)}\)
\(=-a^2\)
a) Ta có: \(\sqrt{27\cdot48\left(1-a^2\right)}\)
\(=\sqrt{3^4\cdot4^2\cdot\left(1-a^2\right)}\)
\(=36\sqrt{1-a^2}\)
c) Ta có: \(\sqrt{5a}\cdot\sqrt{45a}-3a\)
\(=15a-3a=12a\)
b) Ta có: \(B=\dfrac{1}{a-b}\cdot\sqrt{a^4\cdot\left(a-b\right)^2}\)
\(=\dfrac{1}{a-b}\cdot a^2\cdot\left(a-b\right)\)
\(=a^2\)
d) Ta có: \(D=\left(3-a\right)^2-\sqrt{0.2}\cdot\sqrt{180a^2}\)
\(=a^2-6a+9-\sqrt{36a^2}\)
\(=a^2-6a+9-\left|6a\right|\)
\(=\left[{}\begin{matrix}a^2-6a+9-6a\left(a\ge0\right)\\a^2-6a+9+6a\left(a< 0\right)\end{matrix}\right.\)
\(=\left[{}\begin{matrix}a^2-12a+9\\a^2+9\end{matrix}\right.\)
a: Ta có: \(B=\left(\dfrac{6}{a-1}+\dfrac{10-2\sqrt{a}}{a\sqrt{a}-a-\sqrt{a}+1}\right)\cdot\dfrac{\left(\sqrt{a}-1\right)^2}{4\sqrt{a}}\)
\(=\dfrac{6\sqrt{a}-6+10-2\sqrt{a}}{\left(\sqrt{a}-1\right)^2\cdot\left(\sqrt{a}+1\right)}\cdot\dfrac{\left(\sqrt{a}-1\right)^2}{4\sqrt{a}}\)
\(=\dfrac{4\left(\sqrt{a}+1\right)}{\sqrt{a}+1}\cdot\dfrac{1}{4\sqrt{a}}\)
\(=\dfrac{1}{\sqrt{a}}\)
a) \(B=\left(\dfrac{6}{a-1}+\dfrac{10-2\sqrt{a}}{a\sqrt{a}-a-\sqrt{a}+1}\right).\dfrac{\left(\sqrt{a}-1\right)^2}{4\sqrt{a}}=\left(\dfrac{6}{a-1}+\dfrac{10-2\sqrt{a}}{\left(a-1\right)\left(\sqrt{a}-1\right)}\right).\dfrac{\left(\sqrt{a}-1\right)^2}{4\sqrt{a}}=\dfrac{6\left(\sqrt{a}-1\right)+10-2\sqrt{a}}{\left(a-1\right)\left(\sqrt{a}-1\right)}.\dfrac{\left(\sqrt{a}-1\right)^2}{4\sqrt{a}}=\dfrac{4\left(\sqrt{a}+1\right)}{\left(\sqrt{a}-1\right)^2\left(\sqrt{a}+1\right)}.\dfrac{\left(\sqrt{a}-1\right)^2}{4\sqrt{a}}=\dfrac{1}{\sqrt{a}}\)
b) \(C=B.\left(a-\sqrt{a}+1\right)=\dfrac{a-\sqrt{a}+1}{\sqrt{a}}=\sqrt{a}-1+\dfrac{1}{\sqrt{a}}\ge2\sqrt{\sqrt{a}.\dfrac{1}{\sqrt{a}}}-1=1\)(bất đẳng thức Cauchy cho 2 số dương)
b. \(=\left(\dfrac{\sqrt{a}-a+a\left(1-\sqrt{a}\right)}{1-\sqrt{a}}\right):\left(\dfrac{2\sqrt{a}}{1+\sqrt{a}}\right)\)
\(=\left(\dfrac{2\sqrt{a}}{1-\sqrt{a}}\right):\left(\dfrac{2\sqrt{a}}{1+\sqrt{a}}\right)\)
\(=\left(1-\sqrt{a}\right)\left(1+\sqrt{a}\right)\)
\(=1-a\)
\(a.\sqrt{8}-2\sqrt{50}+\sqrt{18}=2\sqrt{2}-10\sqrt{2}+3\sqrt{2}=\sqrt{2}\left(2-10+3\right)=-5\sqrt{2}\)
\(b.\left(\dfrac{\sqrt{a}-a}{1-\sqrt{a}}+\sqrt{a}\right):\dfrac{2\sqrt{a}}{1+\sqrt{a}}\left(đk:a\ge0;a\ne1\right)\)
\(=\left(\sqrt{a}+\sqrt{a}\right).\dfrac{1+\sqrt{a}}{2\sqrt{a}}\)
\(=2\sqrt{a}.\dfrac{1+\sqrt{a}}{2\sqrt{a}}\)
\(=1+\sqrt{a}\)
(Chỗ điều kiện bài b mik thấy a = 0 cũng có thể là nghiệm nên mik sửa lại nhé)
\(A=\dfrac{2-\sqrt{a}-\sqrt{a}-3}{2\sqrt{a}+1}=-1\)
\(B=\dfrac{1}{1-\sqrt{2+\sqrt{3}}}-\dfrac{1}{1-\sqrt{2-\sqrt{3}}}\)
\(=\dfrac{\sqrt{2}}{\sqrt{2}-\sqrt{3}-1}-\dfrac{\sqrt{2}}{\sqrt{2}-\sqrt{3}+1}\)
\(=\dfrac{2-\sqrt{6}+\sqrt{2}-2+\sqrt{6}+\sqrt{2}}{5-2\sqrt{6}-1}\)
\(=\dfrac{2\sqrt{2}}{4-2\sqrt{6}}=\dfrac{1}{\sqrt{2}-\sqrt{3}}=-\sqrt{2}-\sqrt{3}\)
\(A=\left|a-3\right|-3a=3-a-3a=3-4a\)
\(B=4a+3-\left|2a-1\right|=4a+3-2a+1=2a+4\)
\(C=\dfrac{4}{a^2-4}\left|a-2\right|=\dfrac{-4\left(a-2\right)}{\left(a-2\right)\left(a+2\right)}=\dfrac{-4}{a+2}\)
\(D=\dfrac{a^2-9}{12}:\sqrt{\dfrac{\left(a+3\right)^2}{16}}=\dfrac{a^2-9}{12}:\dfrac{\left|a+3\right|}{4}=\dfrac{\left(a-3\right)\left(a+3\right).4}{-12\left(a+3\right)}=\dfrac{3-a}{3}\)
a)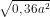
= 
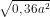= 0,6.│a│
Vì a < 0 nên │a│= -a. Do đó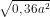
= -0,6a.
b)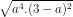
= 
.
= │
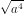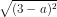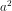│.│3 - a│.
Vì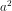
≥ 0 nên │b│= 
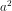. Vì a ≥ 3 nên 3 - a ≤ 0, do đó │3 - a│= a - 3.
Vậy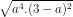
= 
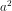(a - 3).
c)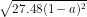
= 
= 
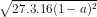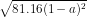= √81.√16.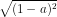
= 9.4.│1 - a│
Vì a > 1 nên 1 - a < 0. Do đó │1 - a│= a -1.
Vậy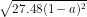
= 36(a - 1).
d)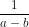
: 
= 
: (
= 
: (
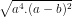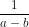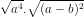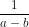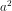.│a - b│)
Vì a > b nên a -b > 0, do đó│a - b│= a - b.
Vậy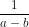
: 
= 
: (
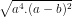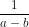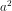(a - b)) = 
.
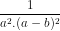a)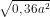
= 
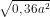= 0,6.│a│
Vì a < 0 nên │a│= -a. Do đó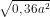
= -0,6a.
b)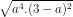
= 
.
= │
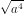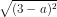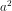│.│3 - a│.
Vì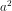
≥ 0 nên │b│= 
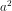. Vì a ≥ 3 nên 3 - a ≤ 0, do đó │3 - a│= a - 3.
Vậy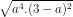
= 
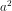(a - 3).
c)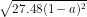
= 
= 
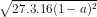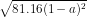= √81.√16.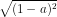
= 9.4.│1 - a│
Vì a > 1 nên 1 - a < 0. Do đó │1 - a│= a -1.
Vậy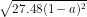
= 36(a - 1).
d)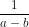
: 
= 
: (
= 
: (
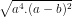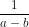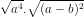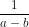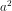.│a - b│)
Vì a > b nên a -b > 0, do đó│a - b│= a - b.
Vậy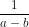
: 
= 
: (
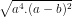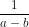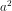(a - b)) = 
.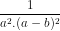