Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) ab2.√3a2b4=ab2.√3√a2b4ab2.3a2b4=ab2.3a2b4
=ab2.√3√a2.√b4=ab2.√3|a|.|b2|=ab2.3a2.b4=ab2.3|a|.|b2|
=ab2.√3(−a).b2=ab2.3(−a).b2 (Do a<0a<0 nên |a|=−a|a|=−a và b≠0b≠0 nên b2>0b2>0 ⇒⇒ ∣∣b2∣∣=b2|b2|=b2)
=−√3=−3.
b) √27(a−3)248=√9(a−3)21627(a−3)248=9(a−3)216
=√9.√(a−3)2√16=3.|a−3|4=9.(a−3)216=3.|a−3|4
=3(a−3)4=3(a−3)4.
(Do a>3a>3 nên |a−3|=a−3|a−3|=a−3)
c) √9+12a+4a2b2=√32+2.3.2a+(2a)2√b29+12a+4a2b2=32+2.3.2a+(2a)2b2
=√(3+2a)2√b2=|3+2a||b|=(3+2a)2b2=|3+2a||b|
=3+2a−b=−2a+3b=3+2a−b=−2a+3b.
(Do a≥−1,5a≥−1,5 ⇒⇒ 3+2a≥03+2a≥0 nên |3+2a|=3+2a|3+2a|=3+2a và b<0b<0 nên |b|=−b|b|=−b)
d) (a−b).√ab(a−b)2=(a−b).√ab√(a−b)2(a−b).ab(a−b)2=(a−b).ab(a−b)2
=(a−b).√ab|a−b|=(a−b).√ab−(a−b)=(a−b).ab|a−b|=(a−b).ab−(a−b)
=−√ab=−ab.
(Do a<b<0a<b<0 nên |a−b|=−(a−b)|a−b|=−(a−b) và ab>0ab>0)
a) ab2.√3a2b4=ab2.√3√a2b4ab2.3a2b4=ab2.3a2b4
=ab2.√3√a2.√b4=ab2.√3|a|.|b2|=ab2.3a2.b4=ab2.3|a|.|b2|
=ab2.√3(−a).b2=ab2.3(−a).b2 (Do a<0a<0 nên |a|=−a|a|=−a và b≠0b≠0 nên b2>0b2>0 ⇒⇒ ∣∣b2∣∣=b2|b2|=b2)
=−√3=−3.
b) √27(a−3)248=√9(a−3)21627(a−3)248=9(a−3)216
=√9.√(a−3)2√16=3.|a−3|4=9.(a−3)216=3.|a−3|4
=3(a−3)4=3(a−3)4.
(Do a>3a>3 nên |a−3|=a−3|a−3|=a−3)
c) √9+12a+4a2b2=√32+2.3.2a+(2a)2√b29+12a+4a2b2=32+2.3.2a+(2a)2b2
=√(3+2a)2√b2=|3+2a||b|=(3+2a)2b2=|3+2a||b|
=3+2a−b=−2a+3b=3+2a−b=−2a+3b.
(Do a≥−1,5a≥−1,5 ⇒⇒ 3+2a≥03+2a≥0 nên |3+2a|=3+2a|3+2a|=3+2a và b<0b<0 nên |b|=−b|b|=−b)
d) (a−b).√ab(a−b)2=(a−b).√ab√(a−b)2(a−b).ab(a−b)2=(a−b).ab(a−b)2
=(a−b).√ab|a−b|=(a−b).√ab−(a−b)=(a−b).ab|a−b|=(a−b).ab−(a−b)
=−√ab=−ab.
(Do a<b<0a<b<0 nên |a−b|=−(a−b)|a−b|=−(a−b) và ab>0ab>0)

a,\(ab^2\sqrt{\dfrac{3}{a^2b^4}}=ab^2.\dfrac{\sqrt{3}}{\sqrt{a^2b^4}}=ab^2.\dfrac{\sqrt{3}}{ab^2}=\sqrt{3}\)
b,\(\sqrt{\dfrac{27\left(a-3\right)^2}{48}}=\dfrac{3\sqrt{3}\left(a-3\right)}{4\sqrt{3}}=\dfrac{3}{4}\left(a-3\right)\)
c,\(\sqrt{\dfrac{9+12a+4a^2}{b^2}}=\dfrac{\sqrt{\left(3+2a\right)^2}}{\sqrt{b^2}}=\dfrac{3+2a}{b}\)
d, \(\left(a-b\right).\sqrt{\dfrac{ab}{\left(a-b\right)^2}}=\left(a-b\right).\dfrac{\sqrt{ab}}{\sqrt{\left(a-b\right)^2}}=\left(a-b\right).\dfrac{\sqrt{ab}}{\left(a-b\right)}=\sqrt{ab}\)

Bài 1:
a: \(=\sqrt{\dfrac{7-4\sqrt{3}}{2-\sqrt{3}}}\cdot\sqrt{2+\sqrt{3}}\)
\(=\sqrt{2-\sqrt{3}}\cdot\sqrt{2+\sqrt{3}}=1\)
Bài 2:
\(VT=\left(4+\sqrt{15}\right)\cdot\left(\sqrt{5}-\sqrt{3}\right)\cdot\sqrt{8-2\sqrt{15}}\)
\(=\left(4+\sqrt{15}\right)\left(8-2\sqrt{15}\right)\)
\(=32-8\sqrt{15}+8\sqrt{15}-30=2\)

a: \(=2ab\cdot\dfrac{-15}{b^2a}=\dfrac{-30}{b}\)
b: \(=\dfrac{2}{3}\cdot\left(1-a\right)=\dfrac{2}{3}-\dfrac{2}{3}a\)
c: \(=\dfrac{\left|3a-1\right|}{\left|b\right|}=\dfrac{3a-1}{b}\)
d: \(=\left(a-2\right)\cdot\dfrac{a}{-\left(a-2\right)}=-a\)

Bài 6:
a: \(\Leftrightarrow\sqrt{x^2+4}=\sqrt{12}\)
=>x^2+4=12
=>x^2=8
=>\(x=\pm2\sqrt{2}\)
b: \(\Leftrightarrow4\sqrt{x+1}-3\sqrt{x+1}=1\)
=>x+1=1
=>x=0
c: \(\Leftrightarrow3\sqrt{2x}+10\sqrt{2x}-3\sqrt{2x}-20=0\)
=>\(\sqrt{2x}=2\)
=>2x=4
=>x=2
d: \(\Leftrightarrow2\left|x+2\right|=8\)
=>x+2=4 hoặcx+2=-4
=>x=-6 hoặc x=2

\(1a.\left(\sqrt{28}-2\sqrt{3}+\sqrt{7}\right)\sqrt{7}+\sqrt{84}=\left(2\sqrt{7}-2\sqrt{3}+\sqrt{7}\right)\sqrt{7}+\sqrt{84}=21-2\sqrt{21}+2\sqrt{21}=21\) \(b.\left(\sqrt{6}+\sqrt{5}\right)^2-\sqrt{120}=11+2\sqrt{30}-2\sqrt{30}=11\)
\(2a.\sqrt{\dfrac{a}{b}}+\sqrt{ab}+\dfrac{a}{b}\sqrt{\dfrac{b}{a}}=\sqrt{\dfrac{a}{b}}+\sqrt{\dfrac{a}{b}.b^2}+\sqrt{\dfrac{a^2}{b^2}.\dfrac{b}{a}}=\sqrt{\dfrac{a}{b}}+b\sqrt{\dfrac{a}{b}}+\sqrt{\dfrac{a}{b}}=\left(2+b\right)\sqrt{\dfrac{a}{b}}\) \(b.\sqrt{\dfrac{m}{1-2x+x^2}}.\sqrt{\dfrac{4m-8mx+4mx^2}{81}}=\sqrt{\dfrac{m}{\left(x-1\right)^2}}.\sqrt{\dfrac{\left(2\sqrt{m}x-2\sqrt{m}\right)^2}{81}}=\dfrac{\sqrt{m}}{\text{|}x-1\text{|}}.\dfrac{\text{|}2\sqrt{m}x-2\sqrt{m}\text{|}}{9}=\dfrac{\sqrt{m}}{\text{|}x-1\text{|}}.\dfrac{2\sqrt{m}\text{|}x-1\text{|}}{9}=\dfrac{2m}{9}\) \(3a.VP=\left(\dfrac{1-a\sqrt{a}}{1-\sqrt{a}}+\sqrt{a}\right)\left(\dfrac{1-\sqrt{a}}{1-a}\right)^2=\left(a+\sqrt{a}+1+\sqrt{a}\right)\left(\dfrac{1}{\sqrt{a}+1}\right)^2=\left(\sqrt{a}+1\right)^2.\dfrac{1}{\left(\sqrt{a}+1\right)^2}=1=VT\)
KL : Vậy đẳng thức được chứng minh.
\(b.VP=\dfrac{a+b}{b^2}.\sqrt{\dfrac{a^2b^4}{a^2+2ab+b^2}}=\dfrac{a+b}{b^2}.\dfrac{b^2\text{|}a\text{|}}{\text{|}a+b\text{|}}=\dfrac{a+b}{b^2}.\dfrac{b^2\text{|}a\text{|}}{a+b}=\text{|}a\text{|}=VT\)
KL : Vậy đẳng thức được chứng minh .
P/s : Dài v ~
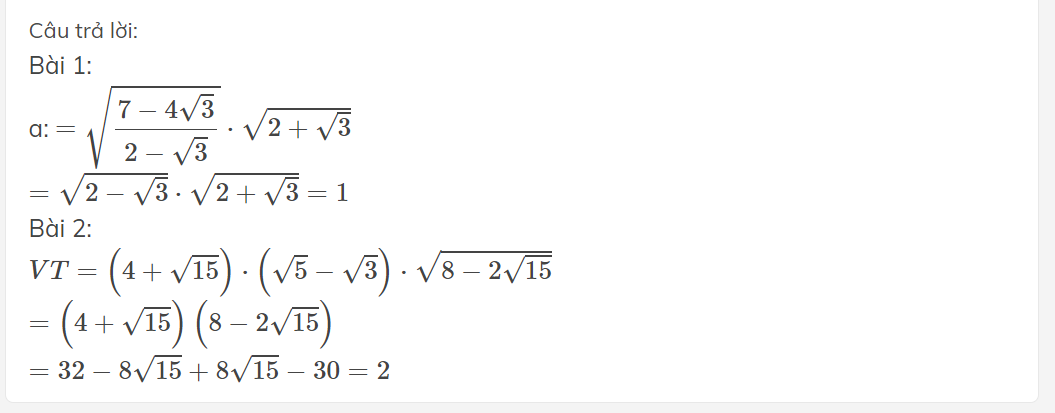
(vì a < 0 nên |a| = -a, b2 > 0 với mọi b ≠ 0 nên |b2| = b2 )
(vì a > 3 nên |a - 3| = a - 3)
Vì b < 0 nên |b| = -b
Vì a ≥ -1,5 nên 3 + 2a ≥ 0. Do đó: |3 + 2a| = 3 + 2a
Vậy:
(vì a < b < 0 và b < 0 nên |a - b| = -(a - b), ab > 0)