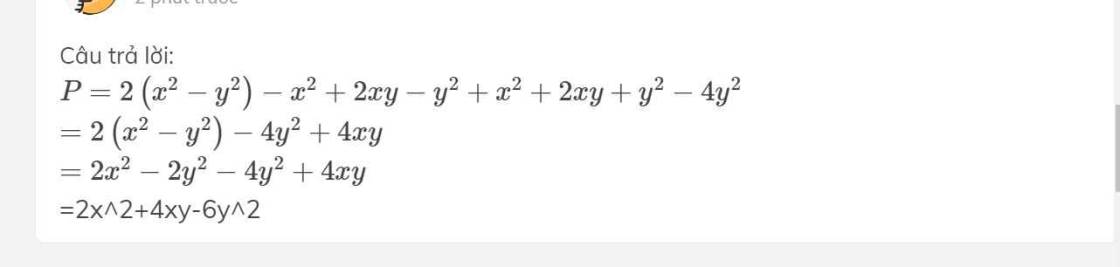MN
0
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
PD
2 tháng 10 2018
1)a)=>x2+y2+2xy-4(x2-y2-2xy)
=>x2+y2+2xy-4.x2+4y2+8xy
=>-3.x2+5y2+10xy
20 tháng 11 2022
\(P=2\left(x^2-y^2\right)-x^2+2xy-y^2+x^2+2xy+y^2-4y^2\)
\(=2\left(x^2-y^2\right)-4y^2+4xy\)
\(=2x^2-2y^2-4y^2+4xy\)
=2x^2+4xy-6y^2
8 tháng 9 2017
Hên xui thôi ( cái này không có chắc lắm )
\(\frac{x^3-xy^3+y^3z-yz^3+z^3x-x^3z}{x^2y-xy^2+y^2z-yz^2+z^2x-zx^2}\)
\(=xy-xy+xy-yz+zx-x^3\)\(z\)\(-\)\(zx^2\)
\(=xy-yz-zx-x^3\)\(z\)
8 tháng 9 2017
phần trên sai rồi cho xin lỗi ( trình bày lại )
bạn ghi lại đề nha
= xy - xy + yz - yz + zx - x^3z - zx^2
= -zx - x^3z
15 tháng 8 2016
=x^3-xy-x^3-x^2y+x^2y--xy
=-2xy
thay x=1\2 va y bang 100 vao Bta duoc
B= -2.1\2.100=-100
BN
3
1 tháng 8 2016
a) \(\left(x-2y\right)^2+\left(x+2y\right)^2=x^2-4xy+4y^2+x^2+4xy+4y^2=2x^2+8y^2\)
b) \(2\left(x-y\right)\left(x+y\right)+\left(x+y\right)^2+\left(x-y\right)^2=2\left(x^2-y^2\right)+x^2+2xy+y^2+x^2-2xy^2+y^2\)
\(=2x^2-2y^2+2x^2+2y^2=4x^2\)
1 tháng 8 2016
\(a,\left(x-2y\right)^2+\left(x+2y\right)^2\)
\(=\left(x^2-4xy+4y^2\right)
+\left(x^2+4xy+4y^2\right)\)
\(=2x^2+8y^2\)
\(b,2\left(x-y\right).\left(x+y\right)+\left(x+y\right)^2+\left(x-y\right)^2\)
\(=2\left(x^2-y^2\right)+\left(x^2+2xy+y^2\right)+\left(x^2-2xy+y^2\right)\)
\(=2x^2-2y^2+2x^2+2y^2\)
\(=4x^2\)
BP
4
A
11 tháng 9 2020
\(P=\left(x^2+2xy\right)^2+2\left(x^2+2xy\right)y^2+y^4\)
\(=x^4+4x^3y+4x^2y^2+2x^2y^2+4xy^3+y^4\)
\(=x^4+y^4+6x^2y^2+4x^3y+4xy^3\)
11 tháng 9 2020
P = ( x2 + 2xy )2 + 2( x2 + 2xy )y2 + y4
= ( x2 + 2xy )2 + 2( x2 + 2xy )y2 + ( y2 )2
= ( x2 + 2xy + y2 )2
= [ ( x + y )2 ]2
= ( x + y )4
29 tháng 6 2019
\(a,\)\(2\left(x-y\right)\left(x+y\right)+\left(x-y\right)^2+\left(x+y\right)^2.\)
\(=\left[\left(x-y\right)+\left(x+y\right)\right]^2=\left(x-y+x+y\right)^2=x^2\)
\(b,\)\(\left(2x-3\right)\left(4x^2+6x+9\right)-\left(54+8x\right)\)
\(=8x^2-27-54-8x=8x^2-8x-81\)
\(c,\)\(\left(3x+y\right)\left(9x^2-3xy+y^2\right)-\left(3x-y\right)\left(9x^2+3xy+y^2\right)\)
\(=27x^3+y^3-\left(27x^3-y^3\right)=2y^3\)
\(d,\)\(\left(a+b+c\right)^2-\left(a-c\right)^2-2ab+2bc\)
\(=a^2+b^2+c^2+2ab+2bc+2ac-a^2+2ac-c^2-2ab+2bc\)
\(=b^2+4bc+4ac\)
