Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

câu a ở phần mẫu của cụm đầu tiên cái \(\left(\sqrt{a+\sqrt{b}}\right)^2\rightarrow\left(\sqrt{a}+\sqrt{b}\right)^2\) giúp em với ạ ( em cảm ơn )

a: \(\sqrt{6+2\sqrt{5}}-\sqrt{6-2\sqrt{5}}\)
\(=\sqrt{5}+1-\sqrt{5}+1\)
=2
c: \(\dfrac{x-y}{\sqrt{x}-\sqrt{y}}=\sqrt{x}+\sqrt{y}\)
d: \(\dfrac{y-2\sqrt{y}+1}{\sqrt{y}-1}=\sqrt{y}-1\)

a) \(\sqrt{\left(2-\sqrt{3}\right)^2}+\sqrt{7+4\sqrt{3}}=\left|2-\sqrt{3}\right|+\sqrt{4+4\sqrt{3}+3}\)
\(=2-\sqrt{3}+\sqrt{\left(2+\sqrt{3}\right)^2}=2-\sqrt{3}+\left|2+\sqrt{3}\right|\)
\(=2-\sqrt{3}+2+\sqrt{3}=4\)
b) \(\left(\frac{a\sqrt{a}+b\sqrt{b}}{\sqrt{a}+\sqrt{b}}-\sqrt{ab}\right):\left(a-b\right)+\frac{2\sqrt{b}}{\sqrt{a}+\sqrt{b}}\)
\(=\left[\frac{\left(\sqrt{a}\right)^3+\left(\sqrt{b}\right)^3}{\sqrt{a}+\sqrt{b}}-\sqrt{ab}\right].\frac{1}{a-b}+\frac{2\sqrt{b}}{\sqrt{a}+\sqrt{b}}\)
\(=\left[\frac{\left(\sqrt{a}+\sqrt{b}\right)\left(a-\sqrt{ab}+b\right)}{\sqrt{a}+\sqrt{b}}-\sqrt{ab}\right].\frac{1}{a-b}+\frac{2\sqrt{b}}{\sqrt{a}+\sqrt{b}}\)
\(=\left(a-\sqrt{ab}+b-\sqrt{ab}\right).\frac{1}{\left(\sqrt{a}-\sqrt{b}\right)\left(\sqrt{a}+\sqrt{b}\right)}+\frac{2\sqrt{b}}{\sqrt{a}+\sqrt{b}}\)
\(=\frac{\left(a-2\sqrt{ab}+b\right)}{\left(\sqrt{a}-\sqrt{b}\right)\left(\sqrt{a}+\sqrt{b}\right)}+\frac{2\sqrt{b}}{\sqrt{a}+\sqrt{b}}\)
\(=\frac{\left(\sqrt{a}-\sqrt{b}\right)^2}{\left(\sqrt{a}-\sqrt{b}\right)\left(\sqrt{a}+\sqrt{b}\right)}+\frac{2\sqrt{b}}{\sqrt{a}+\sqrt{b}}\)
\(=\frac{\sqrt{a}-\sqrt{b}}{\sqrt{a}+\sqrt{b}}+\frac{2\sqrt{b}}{\sqrt{a}+\sqrt{b}}=\frac{\sqrt{a}-\sqrt{b}+2\sqrt{b}}{\sqrt{a}+\sqrt{b}}\)
\(=\frac{\sqrt{a}+\sqrt{b}}{\sqrt{a}+\sqrt{b}}=1\)
a) \(\sqrt{\left(2-\sqrt{3}\right)^2}+\sqrt{7+4\sqrt{3}}\)
\(=\left|2-\sqrt{3}\right|+\sqrt{3+4\sqrt{3}+4}\)
\(=2-\sqrt{3}+\sqrt{\left(\sqrt{3}+2\right)^2}\)
\(=2-\sqrt{3}+\left|\sqrt{3}+2\right|\)
\(=2-\sqrt{3}+\sqrt{3}+2\)
\(=4\)
b) \(\left(\frac{a\sqrt{a}+b\sqrt{b}}{\sqrt{a}+\sqrt{b}}-\sqrt{ab}\right)\div\left(a-b\right)+\frac{2\sqrt{b}}{\sqrt{a}+\sqrt{b}}\)( \(\hept{\begin{cases}a,b\ge0\\a\ne b\end{cases}}\))
\(=\left(\frac{\left(\sqrt{a}+\sqrt{b}\right)\left(a-\sqrt{ab}+b\right)}{\left(\sqrt{a}+\sqrt{b}\right)}-\sqrt{ab}\right)\div\left(a-b\right)+\frac{2\sqrt{b}}{\sqrt{a}+\sqrt{b}}\)
\(=\left(a-\sqrt{ab}+b-\sqrt{ab}\right)\div\left(a-b\right)+\frac{2\sqrt{b}}{\sqrt{a}+\sqrt{b}}\)
\(=\left(a-2\sqrt{ab}+b\right)\div\left(a-b\right)+\frac{2\sqrt{b}}{\sqrt{a}+\sqrt{b}}\)
\(=\frac{a-2\sqrt{ab}+b}{a-b}+\frac{2\sqrt{b}}{\sqrt{a}+\sqrt{b}}\)
\(=\frac{a-2\sqrt{ab}+b}{\left(\sqrt{a}-\sqrt{b}\right)\left(\sqrt{a}+\sqrt{b}\right)}+\frac{2\sqrt{b}\left(\sqrt{a}-\sqrt{b}\right)}{\left(\sqrt{a}-\sqrt{b}\right)\left(\sqrt{a}+\sqrt{b}\right)}\)
\(=\frac{a-2\sqrt{ab}+b+2\sqrt{ab}-2b}{\left(\sqrt{a}-\sqrt{b}\right)\left(\sqrt{a}+\sqrt{b}\right)}\)
\(=\frac{a-b}{a-b}=1\)

đk : \(a\ge0;b\ge0;a\ne b\)
a) \(\dfrac{\sqrt{a}+\sqrt{b}}{\sqrt{a}-\sqrt{b}}+\dfrac{\sqrt{a}-\sqrt{b}}{\sqrt{a}+\sqrt{b}}\) = \(\dfrac{\left(\sqrt{a}+\sqrt{b}\right)^2+\left(\sqrt{a}-\sqrt{b}\right)^2}{\left(\sqrt{a}+\sqrt{b}\right)\left(\sqrt{a}-\sqrt{b}\right)}\)
= \(\dfrac{a+2\sqrt{ab}+b+a-2\sqrt{ab}+b}{a-b}\) = \(\dfrac{2\left(a+b\right)}{a-b}\)
b) đk : \(a\ge0;b\ge0;a\ne b\)
\(\dfrac{a-b}{\sqrt{a}-\sqrt{b}}-\dfrac{\sqrt{a^3}-\sqrt{b^3}}{a-b}\)
= \(\dfrac{\left(\sqrt{a}+\sqrt{b}\right)\left(\sqrt{a}-\sqrt{b}\right)}{\sqrt{a}-\sqrt{b}}-\dfrac{\left(\sqrt{a}-\sqrt{b}\right)\left(a+\sqrt{ab}+b\right)}{\left(\sqrt{a}+\sqrt{b}\right)\left(\sqrt{a}-\sqrt{b}\right)}\)
= \(\dfrac{\sqrt{a}+\sqrt{b}}{1}-\dfrac{a+\sqrt{ab}+b}{\sqrt{a}+\sqrt{b}}\) = \(\dfrac{\left(\sqrt{a}+\sqrt{b}\right)^2-\left(a+\sqrt{ab}+b\right)}{\sqrt{a}+\sqrt{b}}\)
= \(\dfrac{a+2\sqrt{ab}+b-a-\sqrt{ab}-b}{\sqrt{a}+\sqrt{b}}\) = \(\dfrac{\sqrt{ab}}{\sqrt{a}+\sqrt{b}}=\dfrac{\sqrt{ab}\left(\sqrt{a}-\sqrt{b}\right)}{a+b}\)

a) \(\sqrt{16x-8}+\sqrt{36x-18}-\sqrt{64x-32}=\sqrt{10}\)
\(\Leftrightarrow\sqrt{8\left(2x-1\right)}+\sqrt{18\left(2x-1\right)}-\sqrt{32\left(2x-1\right)}=\sqrt{10}\)
\(\Leftrightarrow\sqrt{8}.\sqrt{2x-1}+\sqrt{18}.\sqrt{2x-1}-\sqrt{32}.\sqrt{2x-1}=\sqrt{10}\)
\(\Leftrightarrow\sqrt{2x-1}.\left(\sqrt{8}+\sqrt{18}-\sqrt{32}\right)=\sqrt{10}\)
\(\Leftrightarrow\sqrt{2x-1}.\sqrt{2}=\sqrt{10}\)
\(\Leftrightarrow\sqrt{2x-1}=\sqrt{5}\)
\(\Leftrightarrow2x-1=5\)
\(\Leftrightarrow x=3\)
Vậy ...
b) \(\sqrt{x^2-6x+9}=x+3\)
\(\Leftrightarrow\sqrt{x^2-2.x.3+3^2}=x+3\)
\(\Leftrightarrow\sqrt{\left(x-3\right)^2}=x+3\)
\(\Leftrightarrow\left|x-3\right|=x+3\)
\(\Leftrightarrow x-3=x+3\) hoặc \(x-3=-x-3\)
\(\Leftrightarrow x=0\)
Vậy ...
bài 2 :
A = \(\left(\dfrac{\sqrt{a}+\sqrt{b}}{\sqrt{a}-\sqrt{b}}-\dfrac{4\sqrt{ab}}{a-b}\right)\left(\dfrac{a\sqrt{a}+b\sqrt{b}}{\sqrt{ab}-\left(a+b\right)}\right)\)
\(=\left(\dfrac{\sqrt{a}+\sqrt{b}}{\sqrt{a}-\sqrt{b}}-\dfrac{4\sqrt{ab}}{\left(\sqrt{a}-\sqrt{b}\right)\left(\sqrt{a+\sqrt{b}}\right)}\right)\left(\dfrac{a\sqrt{a}+b\sqrt{b}}{\sqrt{ab}-\left(a+b\right)}\right)\)
\(=\left(\dfrac{\left(\sqrt{a}+\sqrt{b}\right)^2-4\sqrt{ab}}{\left(\sqrt{a}+\sqrt{b}\right)\left(\sqrt{a}-\sqrt{b}\right)}\right)\left(\dfrac{\sqrt{a^3}+\sqrt{b^3}}{\sqrt{ab}-a-b}\right)\)
\(=\left(\dfrac{a+2\sqrt{ab}+b-4\sqrt{ab}}{\left(\sqrt{a}+\sqrt{b}\right)\left(\sqrt{a}-\sqrt{b}\right)}\right)\left(\dfrac{\left(\sqrt{a}+\sqrt{b}\right)\left(a-\sqrt{ab}+b\right)}{-a+\sqrt{ab}-b}\right)\)
\(=\dfrac{a-2\sqrt{ab}+b}{\left(\sqrt{a}+\sqrt{b}\right)\left(\sqrt{a}-\sqrt{b}\right)}.\dfrac{\left(\sqrt{a}+\sqrt{b}\right)\left(a-\sqrt{ab}+b\right)}{-\left(a-\sqrt{ab}+b\right)}\)
\(=\dfrac{\left(\sqrt{a}-\sqrt{b}\right)^2}{\left(\sqrt{a}+\sqrt{b}\right)\left(\sqrt{a}-\sqrt{b}\right)}.\left(-\left(\sqrt{a}+\sqrt{b}\right)\right)\)
\(=\dfrac{\left(\sqrt{a}-\sqrt{b}\right).\left(-1\right).\left(\sqrt{a}+\sqrt{b}\right)}{\sqrt{a}+\sqrt{b}}\)
\(=-\left(\sqrt{a}-\sqrt{b}\right)=\sqrt{b}-\sqrt{a}\)
cuối cùng cũng xong, mong bn phù hộ độ trì cho mk![]()

Ta có : \(a\sqrt{a}-b\sqrt{b}=\left(\sqrt{a}\right)^3-\left(\sqrt{b}\right)^3=\left(\sqrt{a}-\sqrt{b}\right)\cdot\left(a+\sqrt{ab}+b\right)\)Suy ra : a\(\dfrac{a\sqrt{a}-b\sqrt{b}}{\sqrt{a}-\sqrt{b}}=a+\sqrt{ab}+b\)
bạn ơi ! bạn giải thích tại sao nó có thể ra đc hằng đẳng thức trên không
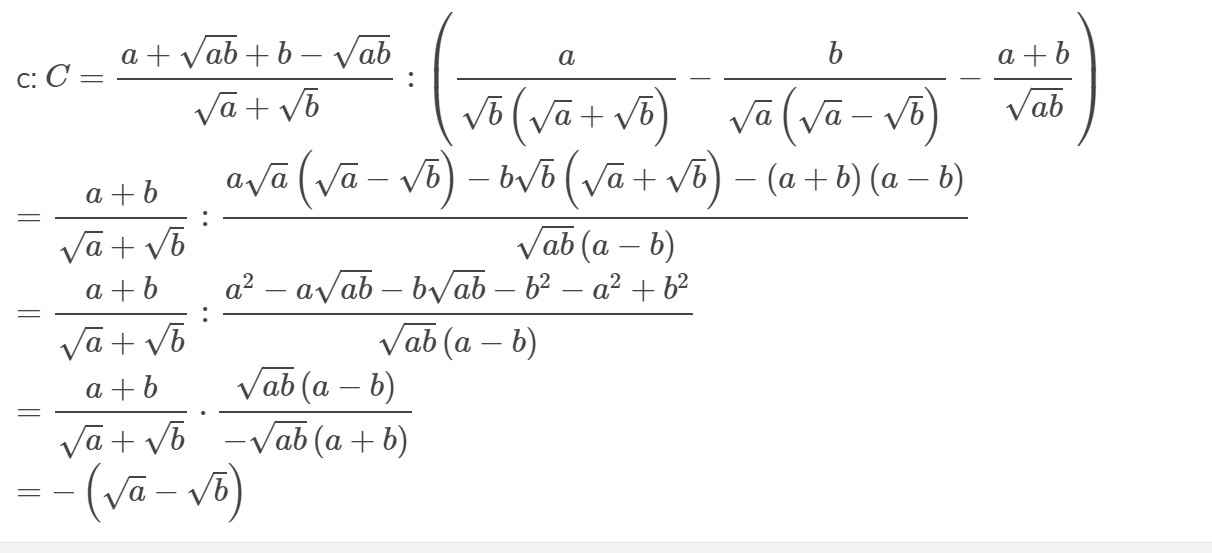
\(\dfrac{a\sqrt{a}-b\sqrt{b}}{\sqrt{a}-\sqrt{b}}=\dfrac{\sqrt{a^3}-\sqrt{b^3}}{\sqrt{a}-\sqrt{b}}\)
\(=\dfrac{\left(\sqrt{a}-\sqrt{b}\right)\left(a+\sqrt{ab}+b\right)}{\sqrt{a}-\sqrt{b}}\)
\(=a+\sqrt{ab}+b\)