Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Có đầy câu hỏi tương tự đáy bạn lên các câu hỏi đó mà xem

a: \(A=\dfrac{a^3+a^2+a^2+a-a-1}{\left(a+1\right)\left(a^2-a+1\right)+2a\left(a+1\right)}\)
\(=\dfrac{\left(a+1\right)\left(a^2+a-1\right)}{\left(a+1\right)\left(a^2+a+1\right)}=\dfrac{a^2+a-1}{a^2+a+1}\)
b: Nếu a là số nguyên âm thì a<0
Vì a2+a=a(a+1) chia hết cho 2 nên \(a^2+a-1;a^2+a+1\) là hai số tự nhiên lẻ liên tiếp
hay A là phân số tối giản

a) Ta có:
\(A=\left(a-4\right)\left(a+5\right)-\left(a-5\right)\left(a+4\right)\)
\(=\left[\left(a-4\right)a+5\left(a-4\right)\right]-\left[\left(a-5\right)a+4\left(a-5\right)\right]\)
\(=\left[a^2-4a+5a-20\right]-\left[a^2-5a+4a-20\right]\)
\(=a^2-4a+5a-20-a^2+5a-4a+20\)
\(=\left(a^2-a^2\right)+\left(-4a+5a+5a-4a\right)+\left(-20+20\right)\)
\(=0+2a+0\)
\(=2a\)
b) Ta có:
\(B=\left(2-a\right)\left(a+7\right)-\left(a-1\right)\left(a+2\right)\)
\(=\left[\left(2-a\right)a+7\left(2-a\right)\right]-\left[\left(a-1\right)a+2\left(a-1\right)\right]\)
\(=\left[2a-a^2+14-7a\right]-\left[a^2-a+2a-2\right]\)
\(=2a-a^2+14-7a-a^2+a-2a+2\)
\(=\left(2a-7a+a-2a\right)-\left(a^2+a^2\right)+\left(14+2\right)\)
\(=-6a-2a^2+16\)

\(A=\left(\frac{1-\left(\sqrt{a}\right)^3}{1-\sqrt{a}}\right)\left(\frac{1-\sqrt{a}}{1-\left(\sqrt{a}\right)^2}\right)^2\)
\(=\left(1+\sqrt{a}+a\right).\frac{1}{\left(1+\sqrt{a}\right)^2}\)
\(=\frac{1+\sqrt{a}+a}{1+2\sqrt{a}+a}\)
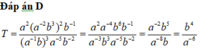

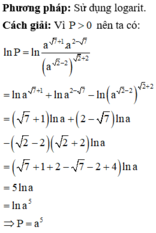
Đáp án A