K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
29 tháng 6 2023
a: =12x^4-6x^3+3x+4x^3-2x^2+1
=12x^4-2x^3-2x^2+3x+1
b: =14x^4+28x^2+6x^2+12x
=14x^4+34x^2+12x
29 tháng 6 2023
`@` `\text {Ans}`
`\downarrow`
\((3x + 1)(4x³ - 2x² + 1)\)
`= 3x(4x^3-2x^2+1) + 4x^3 - 2x^2 + 1`
`= 12x^4 - 6x^3 + 3x + 4x^3 - 2x^2 + 1`
`= 12x^4 + (-6x^3 + 4x^3) - 2x^2 + 3x + 1`
`= 12x^4 - 2x^3 - 2x^2 + 3x + 1`
\((7x² + 3x)(2x + 4)\)
`= 7x^2(2x+4) + 3x(2x+4)`
`= 14x^3 + 28x^2 + 6x^2 + 12x`
`= 14x^3 + (28x^2 + 6x^2)+12x`
`= 14x^3 + 34x^2 + 12x`
`@` `\text {Kaizuu lv uuu}`
6 tháng 11 2021
a: \(A=4x-3x^2+20-15x-9x^2-12x-4+\left(2x+1\right)^3-\left(8x^3-1\right)\)
\(=-12x^2-23x+16+8x^3+12x^2+6x+1-8x^3+1\)
\(=-17x+18\)
H9
HT.Phong (9A5)
CTVHS
14 tháng 4 2023
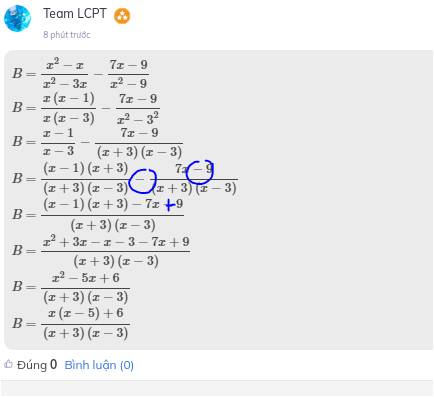
\(B=\dfrac{x^2-x}{x^2-3x}-\dfrac{7x-9}{x^2-9}\)
\(B=\dfrac{x\left(x-1\right)}{x\left(x-3\right)}-\dfrac{7x-9}{x^2-3^2}\)
\(B=\dfrac{x-1}{x-3}-\dfrac{7x-9}{\left(x+3\right)\left(x-3\right)}\)
\(B=\dfrac{\left(x-1\right)\left(x+3\right)}{\left(x+3\right)\left(x-3\right)}-\dfrac{7x-9}{\left(x+3\right)\left(x-3\right)}\)
\(B=\dfrac{\left(x-1\right)\left(x+3\right)-7x-9}{\left(x+3\right)\left(x-3\right)}\)
\(B=\dfrac{x^2+3x-x-3-7x+9}{\left(x+3\right)\left(x-3\right)}\)
\(B=\dfrac{x^2-5x+6}{\left(x+3\right)\left(x-3\right)}\)
\(B=\dfrac{x\left(x-5\right)+6}{\left(x+3\right)\left(x-3\right)}\)
29 tháng 10 2021
\(=7x^2+28x-14x^3+7x^2-28x-6x^2+3x-12\)
\(=-14x^3+8x^2+3x-12\)
29 tháng 10 2021
\(7x\left(x+4\right)-\left(7x+3\right)\left(2x^2-x+4\right)\)
\(=7x^2+28x-14x^3+7x^2-28x-6x^2+3x-12\)
\(=14x^3+8x^2+3x-12\)
H9
HT.Phong (9A5)
CTVHS
7 tháng 10 2023
a) \(C=\left(\dfrac{x}{x^2-x-6}-\dfrac{x-1}{3x^2-4x-15}\right):\dfrac{x^4-2x^2+1}{3x^2+11x+10}\cdot\left(x^2-2x+1\right)\) (ĐK: \(x\ne-\dfrac{5}{3};x\ne3;x\ne-2;x\ne1\))
\(C=\left[\dfrac{x}{\left(x-3\right)\left(x+2\right)}-\dfrac{x-1}{\left(x-3\right)\left(3x+5\right)}\right]:\dfrac{\left(x^2-1\right)^2}{\left(3x+5\right)\left(x+2\right)}\cdot\left(x-1\right)^2\)
\(C=\left[\dfrac{x\left(3x+5\right)}{\left(3x+5\right)\left(x+2\right)\left(x-3\right)}-\dfrac{\left(x-1\right)\left(x+2\right)}{\left(x-3\right)\left(3x+5\right)\left(x+2\right)}\right]\cdot\dfrac{\left(3x+5\right)\left(x+2\right)}{\left(x^2-1\right)^2\left(x-1\right)^2}\)
\(C=\dfrac{3x^2+5x-x^2-2x+x+2}{\left(3x+5\right)\left(x+2\right)\left(x-3\right)}\cdot\dfrac{\left(3x+5\right)\left(x+2\right)}{\left(x^2-1\right)^2\left(x-1\right)^2}\)
\(C=\dfrac{2x^2+4x+2}{\left(3x+5\right)\left(x+2\right)\left(x-3\right)}\cdot\dfrac{\left(3x+5\right)\left(x+2\right)}{\left(x+1\right)^2\left(x-1\right)^4}\)
\(C=\dfrac{2\left(x+1\right)^2}{\left(3x+5\right)\left(x-3\right)\left(x+2\right)}\cdot\dfrac{\left(3x+5\right)\left(x+2\right)}{\left(x+1\right)^2\left(x-1\right)^4}\)
\(C=\dfrac{2}{\left(x-1\right)^4\left(x-3\right)}\)
b) Thay x = 2003 ta có:
\(C=\dfrac{2}{\left(2003-1\right)^4\left(2003-3\right)}=\dfrac{2}{2002^4\cdot2000}=\dfrac{1}{2002^4\cdot1000}\)
c) \(C>0\) khi:
\(\dfrac{2}{\left(x-1\right)^4\left(x-3\right)}>0\) mà: \(\left\{{}\begin{matrix}2>0\\\left(x-1\right)^4>0\end{matrix}\right.\)
\(\Leftrightarrow x-3>0\)
\(\Leftrightarrow x>3\) (đpcm)
KV
27 tháng 12 2022
a) ĐKXĐ: 3x + 6 khác 0
x khác -2
b) A = (x² + 4x + 4)/(3x + 6)
= (x + 2)²/[3(x + 2)]
= (x + 2)/3
c) Khi x = 1/4, ta có:
A = (1/4 + 2)/3
= (9/4)/3
= 3/4
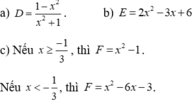
x ≤ 0 nên – 3x ≥ 0 ⇒ |-3x| = -3x
Vậy C = |-3x| + 7x – 4 = -3x + 7x - 4 = 4x - 4