JN
1
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
19 tháng 8 2021
b: Ta có: \(N=a^3+b^3+3ab\)
\(=\left(a+b\right)^3-3ab\left(a+b\right)+3ab\)
\(=1-3ab+3ab\)
=1
26 tháng 9 2021
\(N=a^3+b^3+3ab\)
\(=\left(a+b\right)^3-3ab\left(a+b\right)+3ab\)
=1
26 tháng 9 2021
\(M=\left(a^2+b^2+2-a^2-b^2+2\right)\left[\left(a^2+b^2+2\right)^2+\left(a^2+b^2+2\right)\left(a^2+b^2-2\right)+\left(a^2+b^2-2\right)^2\right]-12\left(a^2+b^2\right)^2\\ M=4\left(a^4+b^4+4+4a^2+4b^2+2a^2b^2+\left(a^2+b^2\right)^2-4+a^4+b^4+4-4a^2-4b^2+2a^2b^2\right)-12\left(a^4+2a^2b^2+b^4\right)\\ M=4\left(3a^4+3b^4+4+6a^2b^2\right)-12\left(a^4+2a^2b^2+b^4\right)\\ M=4\left(3a^4+3b^4+4+6a^2b^2-3a^4-6a^2b^2-3b^4\right)\\ M=4\cdot4=164\)
CM
21 tháng 6 2018
a) Ta có A = 8 ( a 2 + b 2 ) a ( a 2 − 16 b 2 ) . a 2 − 16 b 2 a 2 + b 2 = 8 a
b) Ta có B = 2 t + 2 t + 2 . 4 − t 2 4 − 4 t 2 = 2 − t 2 − 2 t
PA
0
IS
0
KT
20 tháng 7 2018
Bài 1:
a) ĐKXĐ: \(x\ne\pm5\)
\(A=\frac{1}{x+5}+\frac{2}{x-5}-\frac{2x+10}{\left(x+5\right)\left(x-5\right)}\)
\(=\frac{x-5}{\left(x+5\right)\left(x-5\right)}+\frac{2\left(x+5\right)}{\left(x-5\right)\left(x+5\right)}-\frac{2x+10}{\left(x-5\right)\left(x+5\right)}\)
\(=\frac{x-5+\left(2x+10\right)-\left(2x+10\right)}{\left(x-5\right)\left(x+5\right)}\)
\(=\frac{x-5}{\left(x-5\right)\left(x+5\right)}=\frac{1}{x+5}\)
b) \(B=9x^2-42x+49=\left(3x-7\right)^2\)
Tại \(x=-3\)thì: \(B=\left[3.\left(-3\right)-7\right]^2=256\)
KT
20 tháng 7 2018
Bài 2:
a) ĐKXĐ: \(x\ne\pm3\)
\(A=\frac{3}{x+3}+\frac{1}{x-3}-\frac{18}{9-x^2}\)
\(=\frac{3\left(x-3\right)}{\left(x+3\right)\left(x-3\right)}+\frac{x+3}{\left(x-3\right)\left(x+3\right)}+\frac{18}{\left(x-3\right)\left(x+3\right)}\)
\(=\frac{3x-9+x+3+18}{\left(x-3\right)\left(x+3\right)}\)
\(=\frac{4x+12}{\left(x-3\right)\left(x+3\right)}\)
\(=\frac{4\left(x+3\right)}{\left(x-3\right)\left(x+3\right)}=\frac{4}{x-3}\)
b) \(A=4\)\(\Rightarrow\)\(\frac{4}{x-3}=4\)
\(\Rightarrow\)\(4\left(x-3\right)=4\)\(\Leftrightarrow\)\(x-3=1\)\(\Leftrightarrow\)\(x=4\) (t/m ĐKXĐ)
Vậy....
IS
0
19 tháng 1 2022
Bài 1:
a: \(A=\dfrac{x^2-3+x+3}{\left(x-3\right)\left(x+3\right)}\cdot\dfrac{x+3}{x}=\dfrac{x\left(x+1\right)}{x\left(x-3\right)}=\dfrac{x+1}{x-3}\)
b: Để A=3 thì 3x-9=x+1
=>2x=10
hay x=5
Bài 2:
a: \(A=\dfrac{x+x-2-2x-4}{\left(x-2\right)\left(x+2\right)}:\dfrac{x+2-x}{x+2}\)
\(=\dfrac{-6}{x-2}\cdot\dfrac{1}{2}=\dfrac{-3}{x-2}\)
b: Để A nguyên thì \(x-2\in\left\{1;-1;3;-3\right\}\)
hay \(x\in\left\{3;1;5;-1\right\}\)
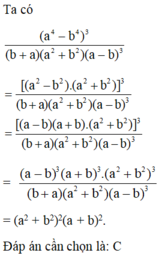
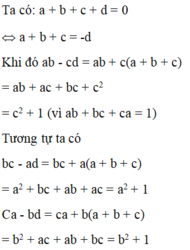
Biểu thức: \(M=\left(a+b\right)^3-\left(a-b\right)^3-b\left(6a^2-b^2\right)\)
\(=a^3+3a^2b+3ab^2+b^3-\left(a^3-3a^2b+3ab^2-b^3\right)-6a^2b+b^3.\)
\(=6a^2b+2b^3-6a^2b+b^3=3b^3\)
Khi b=2 thì M=3*23 =24.