
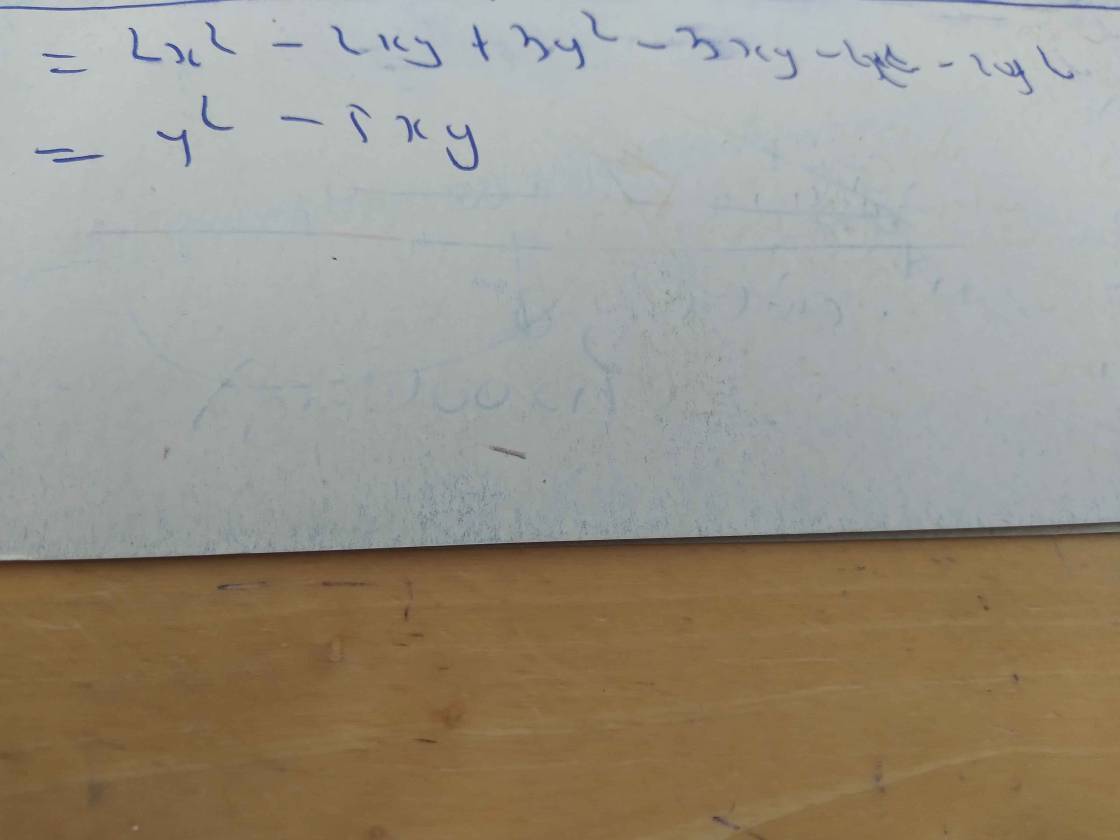
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

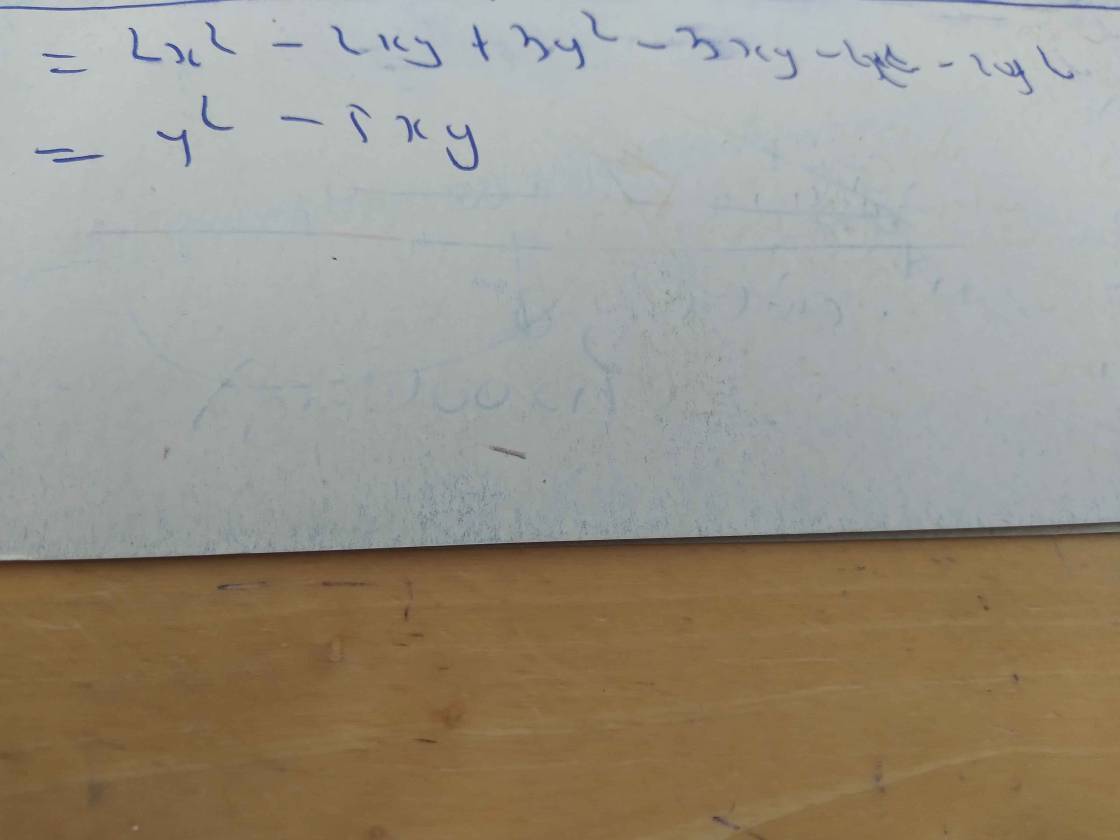

\(a,\left(2x-1\right)^2-\left(x-3\right)\left(x+3\right)-1969\\ =4x^2-4x+1-x^2+9-1969\\ =3x^2-4x-1959\)
\(b,\left(2x-3y\right)\left(2x+3y\right)-\left(2x-y\right)^2\\ =4x^2-9y^2-4x^2+4xy-y^2\\ =8y^2+4xy=4y\left(2y+x\right)\)
\(c,\left(x+3y\right)^2+\left(x+y\right)\left(x-y\right)+280\\ =x^2+6xy+9y^2+x^2-y^2+280\\ =2x^2+8y^2+6xy+280\)
a: \(\left(2x-1\right)^2-\left(x-3\right)\cdot\left(x+3\right)-1969\)
\(=4x^2-4x+1-x^2+9-1969\)
\(=3x^2-4x-1959\)
b: \(\left(2x-3y\right)\left(2x+3y\right)-\left(2x-y\right)^2\)
\(=4x^2-9y^2-4x^2+4xy-y^2\)
\(=-10y^2+4xy\)


Bài 1:
a, (\(x\) - 4).(\(x\) + 4) - (5 - \(x\)).(\(x\) + 1)
= \(x^2\) - 16 - 5\(x\) - 5 + \(x^2\) + \(x\)
= (\(x^2\) + \(x^2\)) - (5\(x\) - \(x\)) - (16 + 5)
= 2\(x^2\) - 4\(x\) - 21
b, (3\(x^2\) - 2\(xy\) + 4) + (5\(xy\) - 6\(x^2\) - 7)
= 3\(x^2\) - 2\(xy\) + 4 + 5\(xy\) - 6\(x^2\) - 7
= (3\(x^2\) - 6\(x^2\)) + (5\(xy\) - 2\(xy\)) - (7 - 4)
= - 3\(x^2\) + 3\(xy\) - 3

\(a,A=\left(2x+y\right)^2-\left(2x-y\right)^2\\ =\left(2x+y-2x+y\right)\left(2x+y+2x-y\right)\\ =2y\cdot4x\\ =8xy\\ b,B=\left(x-2y\right)^2-4y\left(x-2y\right)+4y^2\\ =x^2-4xy+4y^2-4xy+8y^2+4y^2\\ =x^2+16y^2-8xy\\ =\left(x-4y\right)^2\)