
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


\(\sqrt{x^2y^3}+y\sqrt{x^4y}-xy\sqrt{y}\)
\(=xy\sqrt{y}+x^2y\sqrt{y}-xy\sqrt{y}\)
\(=x^2y\sqrt{y}\)

2\(\sqrt{\dfrac{16}{3}}\) - 3\(\sqrt{\dfrac{1}{27}}\) - \(\dfrac{3}{2\sqrt{3}}\)
= \(\dfrac{8}{\sqrt{3}}\) - \(\dfrac{3}{3\sqrt{3}}\) - \(\dfrac{3}{2\sqrt{3}}\)
= \(\dfrac{8}{\sqrt{3}}\) - \(\dfrac{1}{\sqrt{3}}\) - \(\dfrac{3}{2\sqrt{3}}\)
= \(\dfrac{16}{2\sqrt{3}}\) - \(\dfrac{2}{2\sqrt{3}}\) - \(\dfrac{3}{2\sqrt{3}}\)
= \(\dfrac{11}{2\sqrt{3}}\)
= \(\dfrac{11\sqrt{3}}{6}\)
f, 2\(\sqrt{\dfrac{1}{2}}\)- \(\dfrac{2}{\sqrt{2}}\) + \(\dfrac{5}{2\sqrt{2}}\)
= \(\dfrac{2}{\sqrt{2}}\) - \(\dfrac{2}{\sqrt{2}}\) + \(\dfrac{5}{2\sqrt{2}}\)
= \(\dfrac{5}{2\sqrt{2}}\)
= \(\dfrac{5\sqrt{2}}{4}\)
(1 + \(\dfrac{3-\sqrt{3}}{\sqrt{3}-1}\)).(1- \(\dfrac{3+\sqrt{3}}{\sqrt{3}+1}\))
= \(\dfrac{\sqrt{3}-1+3-\sqrt{3}}{\sqrt{3}-1}\).\(\dfrac{\sqrt{3}+1-3+\sqrt{3}}{\sqrt{3}+1}\)
= \(\dfrac{2}{\sqrt{3}-1}\).\(\dfrac{-2}{\sqrt{3}+1}\)
= \(\dfrac{-4}{3-1}\)
= \(\dfrac{-4}{2}\)
= -2

\(A=\left(\dfrac{\sqrt{x}-2}{x-1}-\dfrac{\sqrt{x}+2}{x+2\sqrt{x}+1}\right)\cdot\dfrac{\left(x-1\right)^2}{2}\)
\(=\dfrac{x-\sqrt{x}-2-\sqrt{x}-\sqrt{x}+2}{\left(\sqrt{x}-1\right)^2\cdot\left(\sqrt{x}+1\right)}\cdot\dfrac{\left(x-1\right)^2}{2}\)
\(=-\sqrt{x}\cdot\left(\sqrt{x}+1\right)\)


\(X=\dfrac{3}{\left(\sqrt{x}-2\right)\left(\sqrt{x}+1\right)}+\dfrac{2}{\sqrt{x}+1}+\dfrac{1}{2-\sqrt{x}}\left(đk:x\ge0;x\ne4\right)\)
\(X=\dfrac{3}{\left(\sqrt{x}-2\right)\left(\sqrt{x}+1\right)}+\dfrac{2}{\sqrt{x}+1}-\dfrac{1}{\sqrt{x}-2}\)
\(X=\dfrac{3}{\left(\sqrt{x}-2\right)\left(\sqrt{x}+1\right)}+\dfrac{2\left(\sqrt{x}-2\right)}{\left(\sqrt{x}-2\right)\left(\sqrt{x}+1\right)}-\dfrac{\sqrt{x}+1}{\left(\sqrt{x}-2\right)\left(\sqrt{x}+1\right)}\)
\(X=\dfrac{3+2\sqrt{x}-4-\sqrt{x}-1}{\left(\sqrt{x}-2\right)\left(\sqrt{x}+1\right)}\)
\(X=\dfrac{\sqrt{x}-2}{\left(\sqrt{x}-2\right)\left(\sqrt{x}+1\right)}\)
\(X=\dfrac{1}{\sqrt{x}+1}\)
\(S=\left(\dfrac{1}{x+2\sqrt{x}}+\dfrac{1}{\sqrt{x}-2}\right):\left(\dfrac{1-\sqrt{x}}{x+4\sqrt{x}+4}\right)\left(đk:x\ge0;x\ne1\right)\)
\(S=\left(\dfrac{\sqrt{x}-2}{\sqrt{x}\left(\sqrt{x}+2\right)\left(\sqrt{x}-2\right)}+\dfrac{\sqrt{x}\left(\sqrt{x}+2\right)}{\sqrt{x}\left(\sqrt{x}+2\right)\left(\sqrt{x}-2\right)}\right):\left(\dfrac{1-\sqrt{x}}{x+4\sqrt{x}+4}\right)\)
\(S=\dfrac{\sqrt{x}-2+x+2\sqrt{x}}{\sqrt{x}\left(\sqrt{x}+2\right)\left(\sqrt{x}-2\right)}.\dfrac{x+4\sqrt{x}+4}{1-\sqrt{x}}\)
\(S=\dfrac{x+3\sqrt{x}-2}{\sqrt{x}\left(\sqrt{x}+2\right)\left(\sqrt{x}-2\right)}.\dfrac{\left(\sqrt{x}+2\right)^2}{1-\sqrt{x}}\)
\(S=\dfrac{\left(x+3\sqrt{x}-2\right)\left(\sqrt{x}+2\right)}{\sqrt{x}\left(\sqrt{x}-2\right)\left(1-\sqrt{x}\right)}\)
(đến đoạn này thì trong ngoặc ko tách ra đc nữa nên mik nghĩ là đến đây là xong, nếu sai thì bn nói mik)

Điều kiện xác định : \(x\ge0;y\ge0;\sqrt{x}-\sqrt{y}\ne-3\)
Ta có : \(\frac{x-y+3\sqrt{x}+3\sqrt{y}}{\sqrt{x}-\sqrt{y}+3}=\frac{\left(\sqrt{x}-\sqrt{y}\right)\left(\sqrt{x}+\sqrt{y}\right)+3\left(\sqrt{x}+\sqrt{y}\right)}{\sqrt{x}-\sqrt{y}+3}=\frac{\left(\sqrt{x}+\sqrt{y}\right)\left(\sqrt{x}-\sqrt{y}+3\right)}{\sqrt{x}-\sqrt{y}+3}=\sqrt{x}+\sqrt{y}\)

Trước hết ta sẽ giải quyết phần \(\sqrt{5-2\sqrt{3-\sqrt{3}}}\)
ta có công thức rút gọn sau: \(S+_-2\sqrt{P}\Rightarrow x^2-Sx+P\Leftrightarrow x_1=a;x_2=b\Rightarrow S+2\sqrt{P}=\left(\sqrt{a}+\sqrt{b}\right)^2\)
\(\sqrt{5-2\sqrt{3-\sqrt{3}}}\Rightarrow x^2-5x+3\sqrt{3}=0\left(1\right)\)
\(\left(a=1;b=-5;c=3-\sqrt{3}\right)\)
\(\Delta=b^2-4ac=\left(-5\right)^2-4.1.\left(3-\sqrt{3}\right)=13+4\sqrt{3}>0\)
\(\sqrt{\Delta}=\sqrt{13+4\sqrt{3}}=\sqrt{\left(2\sqrt{3}+1\right)^2}=2\sqrt{3}+1\)
Phương trình (1) có 2 nghiệm phân biệt:
\(x_1=\frac{-b+\sqrt{\Delta}}{2a}=\frac{-\left(-5\right)+2\sqrt{3}+1}{2.1}=3+\sqrt{3}\)
\(x_2=\frac{-b-\sqrt{\Delta}}{2a}=\frac{-\left(-5\right)-\left(2\sqrt{3}-1\right)}{2.1}=2-\sqrt{3}\)
\(\Rightarrow\sqrt{5-2\sqrt{3-\sqrt{3}}}=\sqrt{\left(\sqrt{3+\sqrt{3}}-\sqrt{2-\sqrt{3}}\right)^2}=\sqrt{3+\sqrt{3}}-\sqrt{2-\sqrt{3}}\)
\(F=\sqrt{3+\sqrt{3}}-\sqrt{2-\sqrt{3}}-\sqrt{3+\sqrt{3}}+\sqrt{2+\sqrt{3}}\)
\(\Leftrightarrow F=\sqrt{2+\sqrt{3}}-\sqrt{2-\sqrt{3}}\)
Nhân cả tử và mẫu của hai căn với căn 2
Từ đó ta sẽ được hằng đẳng thức ở tử và rút gọn mất căn:
\(\Leftrightarrow F=\frac{\sqrt{3}+1}{\sqrt{2}}-\frac{\sqrt{3}-1}{\sqrt{2}}=\sqrt{2}\)


Điều kiện xác định \(x\ge\frac{1}{2}\)
\(x^2-8x+10=\left(x+2\right)\sqrt{2x-1}\)
\(\Leftrightarrow x^2-13x=\left(x+2\right)\left(\sqrt{2x-1}-5\right)\)
\(\Leftrightarrow x\left(x-13\right)=\frac{\left(x+2\right)\left(2x-26\right)}{\sqrt{2x-1}+5}\)
\(\Leftrightarrow\left(x-13\right)\left(x-\frac{2\left(x+2\right)}{\sqrt{2x-1}+5}\right)=0\)
Từ đó tiếp tục giải bài toán :)


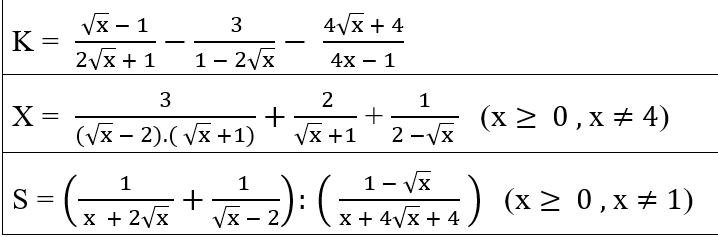
\(B=\dfrac{1}{a-b}\cdot\sqrt{a^4\left(a-b\right)^2}\)
\(=\dfrac{1}{a-b}\cdot a^2\cdot\left(a-b\right)\)
\(=a^2\)