Quan sát hình lăng trụ đứng tam giác ở hình bs.15 rồi điền số thích hợp vào các ô trống trong bảng sau:

K

Khách

Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Mua vip

PT

Pham Trong Bach

25 tháng 3 2019

Quan sát hình lăng trụ đứng tam giác ở hình bs.15 rồi điền số thích hợp vào các ô trống trong bảng sau:

1

CM

Cao Minh Tâm

25 tháng 3 2019

a	9	35	20	63	28
b	40	12	21	16	45
c	41	37	29	65	53
d	8	18	17	24	13
Diện tích một đáy	180	210	210	504	630
Diện tích xung quanh	720	1512	1190	3456	1638
Diện tích toàn phần	1080	1932	1610	4464	2898
Thể tích	1440	3780	3570	12096	8190

Các câu hỏi dưới đây có thể giống với câu hỏi trên

SG

Sách Giáo Khoa

6 tháng 5 2017

Quan sát hình lăng trụ đứng tam giác ở hình bs.15 rồi điền số thích hợp vào các ô trống trong bảng sau :

1

TK

Trần Kiều Anh

10 tháng 5 2017

a	9	35	20	63	28
b	40	12	21	16	45
c	41	37	29	65	53
h	8	18	17	24	13
Diện tích 1 đáy	180	210	210	504	630
Diện tích xung quanh	720	1512	1190	3456	1638
Diện tích toàn phần	1080	1932	1610	4464	2898
Thể tích	1440	3780	3570	12096	8190

SG

Sách Giáo Khoa

24 tháng 4 2017

Quan sát lăng trụ đứng tam giác (h.103) rồi điền số thích hợp vào các ô trống ở bảng sau :

1

HB

Hai Binh

24 tháng 4 2017

Dựa vào công thức: S_xq = 2p.h với p là nửa chu vi, h là chiều cao.

Ta có bảng:

Giải bài 24 trang 111 SGK Toán 8 Tập 2 | Giải toán lớp 8

SG

Sách Giáo Khoa

24 tháng 4 2017

Quan sát các lăng trụ đứng trong hình 96 rồi điền số thích hợp vào các ô trống ở bảng dưới đây :

1

LT

Lê Thiên Anh

24 tháng 4 2017

Giải bài 19 trang 108 SGK Toán 8 Tập 2 | Giải toán lớp 8

SG

Sách Giáo Khoa

24 tháng 4 2017

Quan sát hình 108 rồi điền số thích hợp vào các ô trống ở bảng sau :

1

NL

Nhật Linh

24 tháng 4 2017

Ta có : Diện tích đáy : S = b.h

Thể tích V = S.h₁

+ Ở cột 2 : S = $\frac{1}{2}$ b.h = $\frac{1}{2}$ . 5.2 = 5

V = S .h₁= 5. 8 = 40

+ Ở cột 3 : S = $\frac{1}{2}$ . b.h => h = $\frac{2.S}{b}$ = $\frac{2.12}{6}$ = 4

V = S .h₁= 12.5 = 60

+ Ở cột 4: h = $\frac{2.S}{b}$ = $\frac{2.6}{4}$ = 3

V = S .h₁=>h₁ = $\frac{V}{S}$ = $\frac{12}{6}$ = 2

+ Ở cột 5: V = S .h₁=>h₁ = $\frac{V}{S}$ = $\frac{50}{10}$ = 5

S = $\frac{1}{2}$ b.h = b = $\frac{2.S}{h}$ = $\frac{2.5}{4}$ = $\frac{5}{2}$

Vậy có kết quả sau khi điền vào bảng sau là:

b(cm)	5	6	4	5
h(cm)	2	4	3	4
h₁(cm)	8	5	2	10
Diện tích một đáy(cm)	5	12	6	$\frac{5}{2}$
thể tích	40	60	12	50

SG

Sách Giáo Khoa

24 tháng 4 2017

ABC.A'B'C' là một lăng trụ đứng tam giác (h.98)

a) Những cặp mặt nào song song với nhau ?

b) Những cặp mặt nào vuông góc với nhau ?

a) Sử dụng kí hiệu "//" và "\(\perp\)" để điền vào các ô trống ở bảng sau :

1

LT

Lê Thiên Anh

24 tháng 4 2017

a) Những cặp mặt phẳng song song nhau: (ABC) // (A'B'C')

b) Những cặp mặt phẳng vuông góc với nhau: (ABB'A') ⊥ (A'B'C); (ACC'A') ⊥ (A'B'C'); (BCC'B') ⊥ (A'B'C); (ABB'A') ⊥ (ABC); (ACC'A') ⊥ (ABC); (BCC'B') ⊥ (ABC)

c) Điền vào ô trống:

Giải bài 21 trang 108 SGK Toán 8 Tập 2 | Giải toán lớp 8

SG

Sách Giáo Khoa

6 tháng 5 2017

Quan sát các hình lăng trụ đứng trên hình 122 rồi điền số thích hợp vào các ô trống ở bảng dưới đây :

a) Viết công thức liên hệ giữa n, m, d, c

b) Hình lăng trụ đứng có 20 đỉnh thì có bao nhiêu mặt, bao nhiêu cạnh ?

c) Có thể làm được một hình lăng trụ đứng có 15 đỉnh hay không ?

1

NL

Nguyễn Lê Phước Thịnh

17 tháng 5 2022

Hình lăng trụ	SỐ cạnh của một đáy	Số mặt	SỐ đỉnh	SỐ cạnh
a	6	8	12	18
b	5	7	10	15

a: m=n+2

d=2n;

c=3n

b: Số cạnh của một đáy là:

n=d/2=20/2=10(cạnh)

c: Hình lăng trụ có 20 đỉnh thì

Số mặt là m=n+2=10+2=12(mặt)

Số cạnh là c=3n=30(cạnh)

d: Không thể làm một hình lăng trụ có 15 đỉnh bởi 15 là số lẻ

SG

Sách Giáo Khoa

6 tháng 5 2017

ABCD.XYHK là một lăng trụ đứng, đáy là hình chữ nhật (h.120) a) Quan sát hình và chỉ ra những cặp mặt phẳng song song với nhau b) Những cặp mặt phẳng nào vuông góc với nhau ? c) Hai mặt phẳng (BCHY) và (KXYH) có vuông góc với nhau hay không ? d) Sử dụng kí hiệu // và \(\perp\) để điền vào các ô trống ở bảng sau...

1

NL

Nguyễn Lê Phước Thịnh

17 tháng 5 2022

Tham khảo:

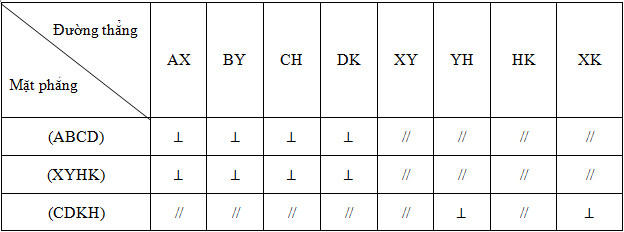
a. Những cặp mặt phẳng song song với nhau là:

mp (ABCD) và mp (XYHK)

mp (ADKX) và mp (BCHY)

mp (ABYX) và mp (CDKH)

b. Những cặp mặt phẳng vuông góc với nhau là:

mp (ABCD) và mp (ADKX); mp (XYHK) và mp (ADKX)

mp (ABCD) và mp (ABYX); mp (XYHK) và mp (ABYX)

mp (ABCD) và mp (BCHY); mp (XYHK) và mp (BCHY)

mp (ABCD) và mp (CDKH); mp (XYHK) và mp (CDKH)

mp (ADKX) và mp (CDKH); mp (ADKX) và mp (ABYX)

mp (BCHY) và mp (CDKH); mp (BCHY) và mp (ABYX)

c. Hai mặt phẳng (BCHY) và (KXYH) vuông góc với nhau.

d:

SG

Sách Giáo Khoa

22 tháng 4 2017

A, B, C và D là những đỉnh của hình hộp chữ nhật cho ở hình 88. Hãy điền số thích hợp vào các ô trống ở bảng sau :

Kết quả bài 12 minh họa công thức quan trọng sau :

\(DA=\sqrt{AB^2+BC^2+CD^2}\)

2

PT

Phạm Thị Trâm Anh

22 tháng 4 2017

Giải bài 12 trang 104 SGK Toán 8 Tập 2 | Giải toán lớp 8

LH

Lưu Hạ Vy

22 tháng 4 2017

Giải bài 12 trang 104 SGK Toán 8 Tập 2 | Giải toán lớp 8

SG

Sách Giáo Khoa

24 tháng 4 2017

A, B, C, D là các đỉnh của một hình hộp chữ nhật. Hãy quan sát hình 145 rồi điền số thích hợp vào các ô trống ở bảng sau :

1

HB

Hai Binh

24 tháng 4 2017

Ta có: Giải bài 55 trang 128 SGK Toán 8 Tập 2 | Giải toán lớp 8 Ta có bảng sau:

Giải bài 55 trang 128 SGK Toán 8 Tập 2 | Giải toán lớp 8

SG

Sách Giáo Khoa

6 tháng 5 2017

Cho hình chóp tứ giác đều (h.146).

Xem hình và điền số thích hợp vào các ô trống còn ở bảng sau :

1

NT

Nguyen Thuy Hoa

5 tháng 7 2017

Hình lăng trụ đứng. Hình chóp đều.