Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Vì ABCD là hình bình hành nên ta có: \(\overrightarrow {AD} = \overrightarrow {BC} \)\(\overrightarrow {AB} + \overrightarrow {AD} = \overrightarrow {AB} + \overrightarrow {BC} = \overrightarrow {AC} \) (đpcm)

Từ giả thiết ta có:
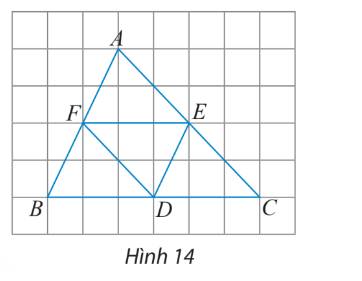
\(AF = FB = ED\); \(AE = EC = FD\); \(BD = DC = EF\)
Từ đó dựa vào hình ta có:
a) Các vectơ bằng vectơ \(\overrightarrow {EF} \)là \(\overrightarrow {DB} \) và \(\overrightarrow {CD} \)
b) Các vectơ đối vectơ \(\overrightarrow {EC} \) là \(\overrightarrow {EA} \) và \(\overrightarrow {DF} \)

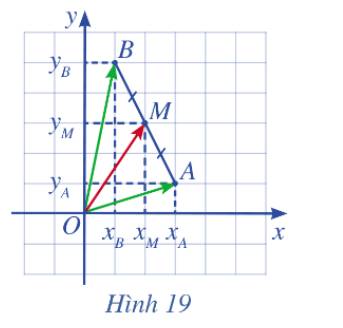
a) Ta có vectơ \(\overrightarrow {OM} \) biểu diễn theo hai vectơ \(\overrightarrow {OA} \) và \(\overrightarrow {OB} \) là: \(\overrightarrow {OM} = \frac{1}{2}\left( {\overrightarrow {OA} + \overrightarrow {OB} } \right)\)
b) Do tọa độ hai điểm A và B là: \(A\left( {{x_A},{y_A}} \right),B\left( {{x_B},{y_B}} \right)\) nên ta có:\(\overrightarrow {OA} = \left( {{x_A},{y_A}} \right),\overrightarrow {OB} = \left( {{x_B},{y_B}} \right)\)
Vậy \(\overrightarrow {OM} = \frac{1}{2}\left( {\overrightarrow {OA} + \overrightarrow {OB} } \right) = \frac{1}{2}\left( {{x_A} + {x_B};{y_A} + {y_B}} \right) = \left( {\frac{{{x_A} + {x_B}}}{2};\frac{{{y_A} + {y_B}}}{2}} \right)\)
Tọa độ điểm M chính là tọa độ của vectơ nên tọa độ M là \(M\left( {\frac{{{x_A} + {x_B}}}{2};\frac{{{y_A} + {y_B}}}{2}} \right)\)

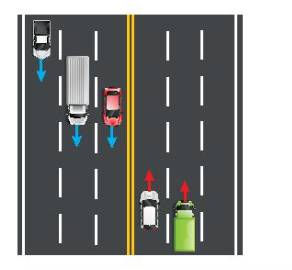
a) Các làn đường song song với nhau: Đúng.
b) Các xe chạy theo cùng một hướng: Sai.
Trong hình 4.5: Có 3 xe chạy theo hướng từ trên xuống dưới, 2 xe chạy thep hướng từ dưới lên trên
c) Hai xe bất kì đều chạy theo cùng một hướng hoặc hai hướng ngược nhau: Đúng.

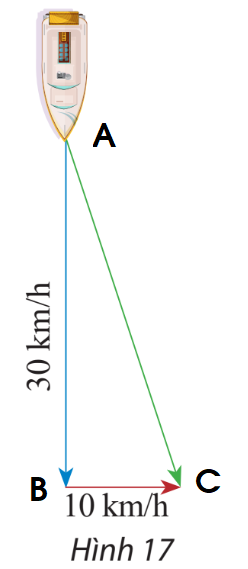
Gọi vecto vận tốc của tàu là \(\overrightarrow {AB} \), vecto vận tốc của dòng nước là vecto \(\overrightarrow {BC} \)
Gọi vecto vận tốc của tàu là \(\overrightarrow {AB} \), vecto vận tốc của dòng nước là vecto \(\overrightarrow {BC} \)
Ta có vecto tổng là \(\overrightarrow F = \overrightarrow {AB} + \overrightarrow {BC} = \overrightarrow {AC} \)
Độ dài vecto tổng là \(\left| {\overrightarrow F } \right| = \left| {\overrightarrow {AC} } \right| = AC = \sqrt {A{B^2} + B{C^2}} = \sqrt {{{30}^2} + {{10}^2}} = 10\sqrt {10} \)(km/h)
Vậy độ dài vecto tổng là \(10\sqrt {10} \)(km/h).
Ta có vecto tổng là \(\overrightarrow F = \overrightarrow {AB} + \overrightarrow {BC} = \overrightarrow {AC} \)
Độ dài vecto tổng là \(\left| {\overrightarrow F } \right| = \left| {\overrightarrow {AC} } \right| = AC = \sqrt {A{B^2} + B{C^2}} = \sqrt {{{30}^2} + {{10}^2}} = 10\sqrt {10} \)(km/h)
Vậy độ dài vecto tổng là \(10\sqrt {10} \)(km/h).

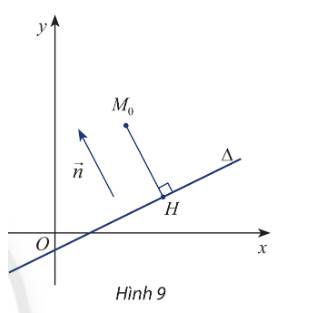
a) Ta có: \(\overrightarrow n \) và \(\overrightarrow {H{M_0}} = \left( {{x_0} - {x_H};{y_0} - {y_H}} \right)\)
Mà H là hình chiếu vuông góc của \({M_0}\) trên \(\Delta \) nên \(H{M_0} \bot \Delta \)
Mặt khác vectơ pháp tuyến \(\overrightarrow n \) cùng vuông góc với \(\Delta \)
Suy ra \(\overrightarrow n \) và \(\overrightarrow {H{M_0}} \)cùng phương (đpcm)
b) Ta có: \(\overrightarrow n = (a;b)\) và \(\overrightarrow {H{M_0}} = \left( {{x_0} - {x_H};{y_0} - {y_H}} \right)\)
Suy ra \(p = \overrightarrow n .\overrightarrow {H{M_0}} = a\left( {{x_0} - {x_H}} \right) + b\left( {{y_0} - {y_H}} \right) = a{x_0} + b{y_0} - \left( {a{x_H} + b{y_H}} \right)\) (1)
Mà H thuộc đường thẳng \(\Delta \) nên tọa độ điểm H thỏa mãn phương trình đường thẳng \(\Delta \)
Thay tọa độ điểm H vào phương trình \(\Delta :ax + by + c = 0\left( {{a^2} + {b^2} > 0} \right)\) ta có:
\(a{x_H} + b{y_H} + c = 0 \Leftrightarrow c = - \left( {a{x_H} + b{y_H}} \right)\)
Thay \(c = - \left( {a{x_H} + b{y_H}} \right)\) vào (1) ta có
\(p = a{x_0} + b{y_0} + c\) (đpcm)
c) Ta có: \(p = \overrightarrow n .\overrightarrow {H{M_0}} \Leftrightarrow \overrightarrow {H{M_0}} = \frac{p}{{\overrightarrow n }} \Rightarrow \left| {\overrightarrow {H{M_0}} } \right| = \left| {\frac{p}{{\overrightarrow n }}} \right| \Rightarrow \left| {\overrightarrow {H{M_0}} } \right| = \frac{{\left| p \right|}}{{\left| {\overrightarrow n } \right|}}\)

a) Ta có:
Giá của vectơ \(\overrightarrow {AB} \) là đường thẳng AB
Giá của vectơ \(\overrightarrow {CD} \) là đường thẳng CD.
Dễ thấy: AB // CD do đó hai vectơ này cùng phương.
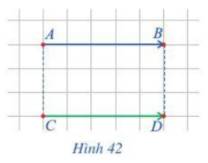
b) Quan sát hình 42, ta thấy cả hai vectơ \(\overrightarrow {AB} \) và \(\overrightarrow {CD} \) cùng hướng sang phải
Như vậy hai vectơ này cùng hướng.
c) Ta có: \(|\overrightarrow {AB} |\; = AB\); \(|\overrightarrow {CD} |\; = CD\) và AB = CD (cùng dài 5 ô vuông)
Vậy độ dài của hai vectơ là bằng nhau.

Dễ thấy:
\(AD = BC\) nhưng \(AD\) và \(BC\) không song song với nhau. Do đó hai vectơ \(\overrightarrow {AD} \) và \(\overrightarrow {BC} \) không bằng nhau.
\(CD > AB\) do đó hai vectơ \(\overrightarrow {AB} \) và \(\overrightarrow {CD} \) không bằng nhau.
\(AC\) và \(BD\) không song song với nhau. Do đó hai vectơ \(\overrightarrow {AC} \) và \(\overrightarrow {BD} \) không bằng nhau.

a) Phương trình tham số của đường thẳng \(d:\left\{ \begin{array}{l}x = 1 + 40t\\y = 1 + 30t\end{array} \right.\)
b) Thay \(t = 2\) vào phương trình\(d:\left\{ \begin{array}{l}x = 1 + 40t\\y = 1 + 30t\end{array} \right.\) ta được \(\left\{ \begin{array}{l}x = 1 + 40.2 = 81\\y = 1 + 30.2 = 61\end{array} \right.\)
Vậy khi \(t = 2\) thì tọa độ của ô tô là \(\left( {81;61} \right)\)
Thay \(t = 4\) vào phương trình\(d:\left\{ \begin{array}{l}x = 1 + 40t\\y = 1 + 30t\end{array} \right.\) ta được \(\left\{ \begin{array}{l}x = 1 + 40.4 = 161\\y = 1 + 30.4 = 121\end{array} \right.\)
Vậy khi \(t = 4\) thì tọa độ của ô tô là \(\left( {161;121} \right)\)
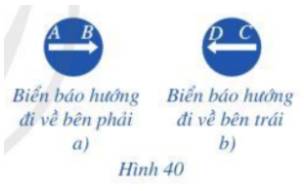





Giá của vectơ \(\overrightarrow {AB} \) là đường thẳng AB
Giá của vectơ \(\overrightarrow {CD} \) là đường thẳng CD.
Dễ thấy: đường thẳng AB trùng với đường thẳng CD.
Do đó hai vectơ \(\overrightarrow {AB} \) và \(\overrightarrow {CD} \) có cùng phương.
Lại có: vectơ \(\overrightarrow {AB} \) chỉ hướng đi về bên phải còn vectơ \(\overrightarrow {CD} \) chỉ hướng đi về bên trái.
Vậy hai vectơ \(\overrightarrow {AB} \) và \(\overrightarrow {CD} \) có ngược hướng.