Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

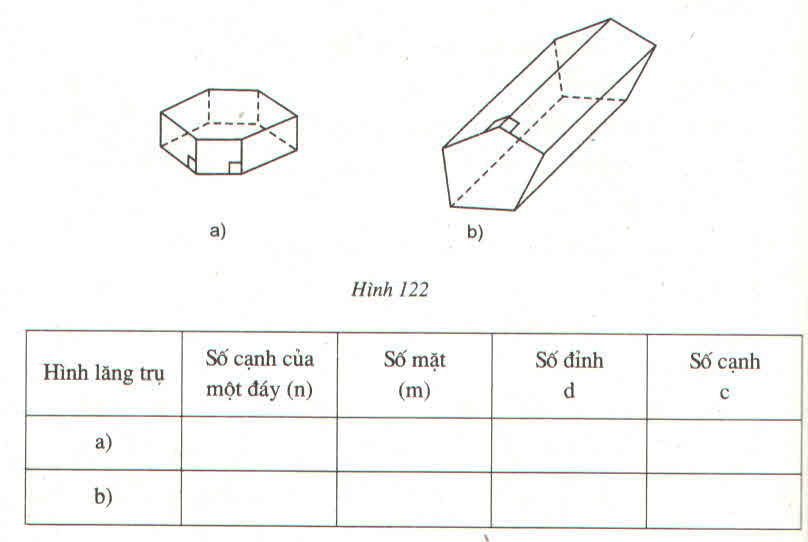
| Hình lăng trụ | Số cạnh của một đáy (n) | Số mặt (m) | Số đỉnh (d) | Số cạnh (c) |
| a) | 6 | 8 | 12 | 18 |
| b) | 5 | 7 | 10 | 15 |
Số cạnh của một đáy là: n = d/2 = 20/2 = 10 cạnh
Hình lăng trụ có 20 đỉnh thì :
Số mặt là m = n + 2 = 10 + 2 = 12 mặt
Số cạnh là c = 3n = 3.10 = 30 cạnh

| Hình lăng trụ | Số cạnh của một đáy (n) | Số mặt (m) | Số đỉnh (d) | Số cạnh (c) |
| a) | 6 | 8 | 12 | 18 |
| b) | 5 | 7 | 10 | 15 |
Không thể làm một hình lăng trụ đứng có 15 đỉnh vì d = 2n (số đỉnh của hình lăng trụ là một số chẵn)

| Hình lăng trụ | Số cạnh của một đáy (n) | Số mặt (m) | Số đỉnh (d) | Số cạnh (c) |
| a) | 6 | 8 | 12 | 18 |
| b) | 5 | 7 | 10 | 15 |
Công thức liên hệ giữa m,n,d,c :
m = n + 2 ; d = 2n; c = 3n

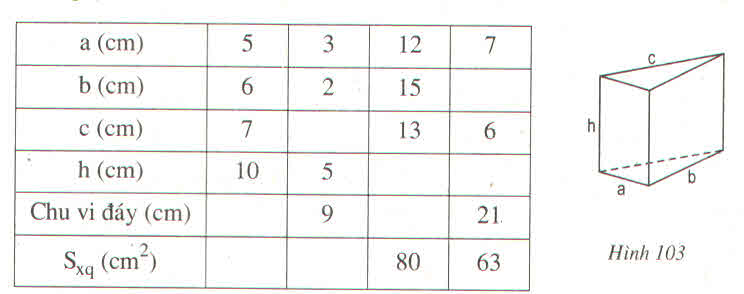
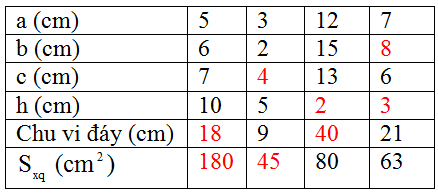
| a | 9 | 35 | 20 | 63 | 28 |
| b | 40 | 12 | 21 | 16 | 45 |
| c | 41 | 37 | 29 | 65 | 53 |
| h | 8 | 18 | 17 | 24 | 13 |
| Diện tích 1 đáy | 180 | 210 | 210 | 504 | 630 |
| Diện tích xung quanh | 720 | 1512 | 1190 | 3456 | 1638 |
| Diện tích toàn phần | 1080 | 1932 | 1610 | 4464 | 2898 |
| Thể tích | 1440 | 3780 | 3570 | 12096 | 8190 |

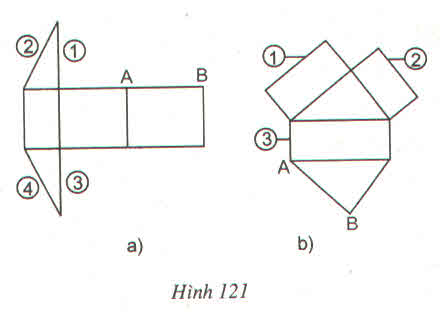
a: Hình a có 5 mặt ghép thành lăng trụ đứng có đáy là tam giác thì cạnh 2 sẽ được ghép với cạnh AB tạo thành lăng trụ đứng
b: Hình b có 5 mặt ghép thành lăng trụ đứng có đáy là tam giác có cạnh AB nên cạnh số 1 ghép với cạnh AB ta được lăng trụ đứng

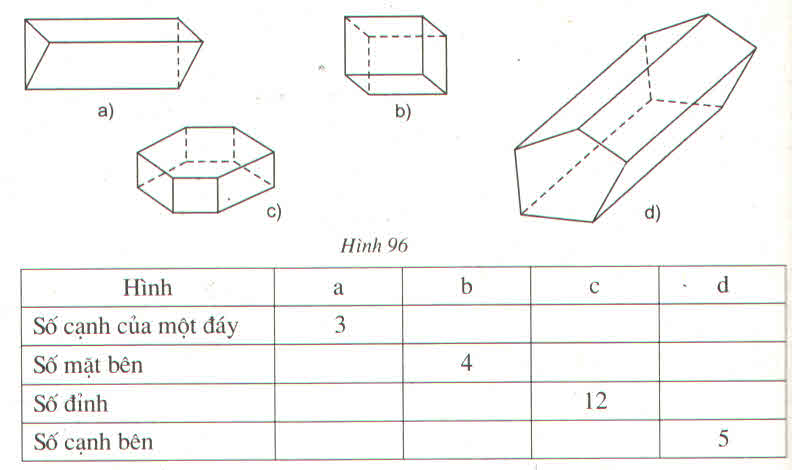
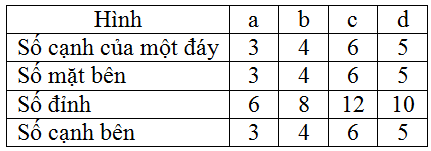
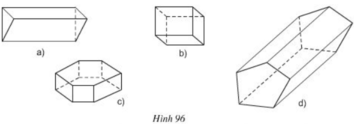
| Hình | a | b | c | d |
| Số cạnh của một đáy | 3 | 4 | 6 | 5 |
| Số mặt bên | 3 | 4 | 6 | 5 |
| Số đỉnh | 6 | 8 | 12 | 10 |
| Số cạnh bên | 3 | 4 | 6 | 5 |

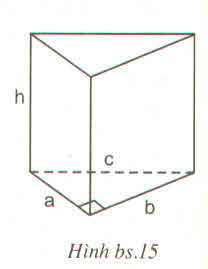
a) Đáy của hình lăng trụ đứng là một tam giác vuông cân
b) Các mặt bên nhận được không phải tất cả là hình vuông
\(\Bigg(\) hai hình vuông và một hình chữ nhật \(\Bigg)\)


a: m=n+2
d=2n;
c=3n
b: Số cạnh của một đáy là:
n=d/2=20/2=10(cạnh)
c: Hình lăng trụ có 20 đỉnh thì
Số mặt là m=n+2=10+2=12(mặt)
Số cạnh là c=3n=30(cạnh)
d: Không thể làm một hình lăng trụ có 15 đỉnh bởi 15 là số lẻ