Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a, \(\Delta=25-8=17\)>0 Vậy pt có 2 nghiệm pb
\(x=\dfrac{5\pm\sqrt{17}}{4}\)
b, \(\Delta=16-16=0\)Vậy pt có nghiệm kép
\(x_1=x_2=\dfrac{1}{4}\)
c, \(\Delta=1-4.2.5< 0\)Vậy pt vô nghiệm
d, \(\Delta=4+4.24=100>0\)Vậy pt có 2 nghiệm pb
\(x=\dfrac{-2-10}{-6}=2;x=\dfrac{-2+10}{-6}=-\dfrac{4}{3}\)

Mấy bài này đều là toán lớp 8 mà. Mình mới lớp 8 mà cũng làm được nữa là bạn lớp 9 mà không làm được afk?
a) (3x - 2)(4x + 5) = 0
⇔ 3x - 2 = 0 hoặc 4x + 5 = 0
1) 3x - 2 = 0 ⇔ 3x = 2 ⇔ x = 2/3
2) 4x + 5 = 0 ⇔ 4x = -5 ⇔ x = -5/4
Vậy phương trình có tập nghiệm S = {2/3;−5/4}
b) (2,3x - 6,9)(0,1x + 2) = 0
⇔ 2,3x - 6,9 = 0 hoặc 0,1x + 2 = 0
1) 2,3x - 6,9 = 0 ⇔ 2,3x = 6,9 ⇔ x = 3
2) 0,1x + 2 = 0 ⇔ 0,1x = -2 ⇔ x = -20.
Vậy phương trình có tập hợp nghiệm S = {3;-20}
c) (4x + 2)(x2 + 1) = 0 ⇔ 4x + 2 = 0 hoặc x2 + 1 = 0
1) 4x + 2 = 0 ⇔ 4x = -2 ⇔ x = −1/2
2) x2 + 1 = 0 ⇔ x2 = -1 (vô lí vì x2 ≥ 0)
Vậy phương trình có tập hợp nghiệm S = {−1/2}
d) (2x + 7)(x - 5)(5x + 1) = 0
⇔ 2x + 7 = 0 hoặc x - 5 = 0 hoặc 5x + 1 = 0
1) 2x + 7 = 0 ⇔ 2x = -7 ⇔ x = −7/2
2) x - 5 = 0 ⇔ x = 5
3) 5x + 1 = 0 ⇔ 5x = -1 ⇔ x = −1/5
Vậy phương trình có tập nghiệm là S = {−7/2;5;−1/5}

Bài 1:
a) \(\Delta=b^2-4ac=\left(-5\right)^2-4\cdot2\cdot1=25-8=17\)
Vì Δ>0 nên phương trình \(2x^2-5x+1=0\) có hai nghiệm là:
\(\left\{{}\begin{matrix}x_1=\frac{-b-\sqrt{\Delta}}{2a}\\x_2=\frac{-b+\sqrt{\Delta}}{2a}\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x_1=\frac{5-\sqrt{17}}{2\cdot2}=\frac{5-\sqrt{17}}{4}\\x_2=\frac{5+\sqrt{17}}{2\cdot2}=\frac{5+\sqrt{17}}{4}\end{matrix}\right.\)
Vậy: \(S=\left\{\frac{5-\sqrt{17}}{4};\frac{5+\sqrt{17}}{4}\right\}\)
b) Ta có: \(4x^2+4x+1=0\)
\(\Leftrightarrow\left(2x+1\right)^2=0\)
\(\Leftrightarrow2x+1=0\)
\(\Leftrightarrow2x=-1\)
hay \(x=-\frac{1}{2}\)
Vậy: \(S=\left\{\frac{-1}{2}\right\}\)
c) Ta có: \(-3x^2+2x+8=0\)
\(\Leftrightarrow-3x^2+6x-4x+8=0\)
\(\Leftrightarrow-3x\left(x-2\right)-4\left(x-2\right)=0\)
\(\Leftrightarrow\left(x-2\right)\left(-3x-4\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x-2=0\\-3x-4=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=2\\-3x=4\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=2\\x=\frac{-4}{3}\end{matrix}\right.\)
Vậy: \(S=\left\{2;\frac{-4}{3}\right\}\)
d) Ta có: \(5x^2-6x-1=0\)
\(\Delta=b^2-4\cdot a\cdot c=\left(-6\right)^2-4\cdot5\cdot\left(-1\right)=56\)
Vì Δ>0 nên phương trình \(5x^2-6x-1=0\) có hai nghiệm là:
\(\left\{{}\begin{matrix}x_1=\frac{-b-\sqrt{\Delta}}{2a}\\x_2=\frac{-b+\sqrt{\Delta}}{2a}\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x_1=\frac{6-\sqrt{56}}{2\cdot5}=\frac{3-\sqrt{14}}{5}\\x_2=\frac{6+\sqrt{56}}{2\cdot5}=\frac{3+\sqrt{14}}{5}\end{matrix}\right.\)
Vậy: \(S=\left\{\frac{3-\sqrt{14}}{5};\frac{3+\sqrt{14}}{5}\right\}\)
e) Ta có: \(-3x^2+14x-8=0\)
\(\Leftrightarrow-3x^2+12x+2x-8=0\)
\(\Leftrightarrow-3x\left(x-4\right)+2\left(x-4\right)=0\)
\(\Leftrightarrow\left(x-4\right)\left(-3x+2\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x-4=0\\-3x+2=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=4\\-3x=-2\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=4\\x=\frac{2}{3}\end{matrix}\right.\)
Vậy: \(S=\left\{4;\frac{2}{3}\right\}\)
g) Ta có: \(-7x^2+4x-3=0\)
\(\Delta=b^2-4ac=4^2-4\cdot\left(-7\right)\cdot\left(-3\right)=-68\)
Vì Δ<0 nên phương trình \(-7x^2+4x-3=0\) không có nghiệm
Vậy: S=∅

\(x^2-2-2\sqrt{4x-7}=0\)
\(\Leftrightarrow\left(4x-7-2\sqrt{4x-7}+1\right)+\left(x^2-4x+4\right)=0\)
\(\Leftrightarrow\left(\sqrt{4x-7}-1\right)^2+\left(x-2\right)^2=0\)
\(\Rightarrow\left[{}\begin{matrix}\sqrt{4x-7}-1=0\\x-2=0\end{matrix}\right.\)
Tự làm tiếp nhé.
. . .
\(4x^2-5x+1+2\sqrt{x-1}=0\)
\(\Leftrightarrow\left(x-1\right)\left(4x-1\right)+2\sqrt{x-1}=0\)
\(\Leftrightarrow\sqrt{x-1}\left[\left(4x-1\right)\sqrt{x-1}+2\right]=0\)
\(\Rightarrow x=1\)
. . .
\(\sqrt{x^2-4x+4}+\sqrt{x^2-6x+9}=1\)
\(\Leftrightarrow\sqrt{\left(x-2\right)^2}+\sqrt{\left(x-3\right)^2}=1\)
\(\Leftrightarrow\left|x-2\right|+\left|x-3\right|=1\)
\(VT=\left|x-2\right|+\left|3-x\right|\ge\left|x-2+3-x\right|=1=VP\)
Dấu "=" xảy ra khi \(\left(x-2\right)\left(3-x\right)\ge0\)
Đến đây lập bảng xét dấu
. . .
\(x^2-x+2=2\sqrt{x^2-x+1}\)
\(\Leftrightarrow\left(\sqrt{x^2-x+1}-1\right)^2=0\)
Tự làm tiếp nhé.
\(\sqrt{3x+1}-\sqrt{6-x}+3x^2-14x-8=0\)
\(\Leftrightarrow\left(\sqrt{3x+1}-4\right)+\left(1-\sqrt{6-x}\right)+\left(3x^2-14-5\right)=0\)
\(\Leftrightarrow\dfrac{3x+1-16}{\sqrt{3x+1}+4}+\dfrac{1-6+x}{1+\sqrt{6-x}}+\left(x-5\right)\left(3x+1\right)=0\)
\(\Leftrightarrow\dfrac{3\left(x-5\right)}{\sqrt{3x+1}+4}+\dfrac{x-5}{1+\sqrt{6-x}}+\left(x-5\right)\left(3x+1\right)=0\)
\(\Leftrightarrow\left(\dfrac{3}{\sqrt{3x+1}+4}+\dfrac{1}{1+\sqrt{6-x}}+3x+1\right)\left(x-5\right)=0\)
\(\Rightarrow x=5\)
. . .
\(\sqrt{2x^2-4x+5}-x+4=0\)
\(\Leftrightarrow\sqrt{2x^2-4x+5}=x-4\)
\(\Leftrightarrow\left\{{}\begin{matrix}x-4\ge0\\2x^2-4x+5=x^2-8x+16\end{matrix}\right.\)
Tự làm tiếp nhé.
. . .
\(\sqrt{2x+3}+\sqrt{x-1}=\sqrt{x+6}\)
\(\Leftrightarrow\sqrt{2x+3}=\sqrt{x+6}-\sqrt{x-1}\)
\(\Leftrightarrow2x+3=x+6-2\sqrt{\left(x+6\right)\left(x-1\right)}+x-1\)
\(\Leftrightarrow2\sqrt{x^2+5x-6}=2\)
\(\Leftrightarrow x^2+5x-6=1\)
Tự làm tiếp nhé.
. . .
\(x+y+\dfrac{1}{2}=\sqrt{x}+\sqrt{y}\)
\(\Leftrightarrow\left(x-\sqrt{x}+\dfrac{1}{4}\right)+\left(y-\sqrt{y}+\dfrac{1}{4}\right)=0\)
\(\Leftrightarrow\left(\sqrt{x}-\dfrac{1}{2}\right)^2+\left(\sqrt{y}-\dfrac{1}{2}\right)^2=0\)
Tự làm tiếp nhé.

a) ta có : \(S=x_1+x_2=\dfrac{7}{2};P=x_1x_2=1\)
b) ta có \(S=x_1+x_2=\dfrac{-9}{2};P=x_1x_2=\dfrac{7}{2}\)
c) ta có : \(S=x_1+x_2=\dfrac{-4}{2-\sqrt{3}};P=x_1x_2=\dfrac{2+\sqrt{2}}{2-\sqrt{3}}\)
d) ta có : \(S=x_1+x_2=\dfrac{3}{1,4}=\dfrac{15}{7};P=x_1x_2=\dfrac{1,2}{1,4}=\dfrac{6}{7}\)
e) ta có : \(S=x_1+x_2=\dfrac{-1}{5};P=x_1x_2=\dfrac{2}{5}\)
a) Theo hệ thức Vi-ét :
x1+x2=\(\frac{-b}{a}=\frac{7}{2}\)
x1x2=\(\frac{c}{a}=\frac{2}{2}=1\)
b) theo hệ thức Vi-ét:
x1+x2=\(\frac{-b}{a}=\frac{-9}{2}\)
x1x2=\(\frac{c}{a}=\frac{7}{2}\)
c)x1+x2=\(\frac{-b}{a}=\frac{-4}{2-\sqrt{3}}=-8-4\sqrt{3}\)
x1x2=\(\frac{c}{a}=\frac{2+\sqrt{2}}{2-\sqrt{3}}\)
d) x1+x2=\(\frac{-b}{a}=\frac{3}{1,4}=\frac{15}{7}\)
x1x2=\(\frac{c}{a}=\frac{1,2}{1,4}=\frac{6}{7}\)
e) x1+x2=\(\frac{-b}{a}=\frac{-1}{5}\)
x1x2=\(\frac{c}{a}=\frac{2}{5}\)



a) 4x2 + 4x + 1 = 0 có a = 4, b = 4, b' = 2, c = 1
∆' = 22 – 4 . 1 = 0: Phương trình có nghiệm kép
x1 = x2 =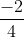 =
= 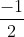
b) 13852x2 – 14x + 1 = 0 có a = 13852, b = -14, b’ = -7, c = 1
∆’ = (-7)2 – 13852 . 1 = 49 – 13852 < 0
Phương trình vô nghiệm.
c) 5x2 – 6x + 1 = 0 có a = 5, b = -6, b’ = -3, c = 1
∆’ = (-3)2 – 5 . 1 = 4, √∆’ = 2
x1 = = 1; x2 =
= 1; x2 = 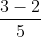 =
= 
d) -3x2 + 4√6x + 4 = 0 có a = -3, b = 4√6, b’ = 2√6, c = 4.
∆’ = (2√6)2 – (-3) . 4 = 24 + 12 = 36, √∆’ = 6
X1 = = ;
= ;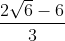 , x2 =
, x2 = 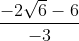 =
= 