HT
2
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
PT
1
TT
1
AH
Akai Haruma
Giáo viên
5 tháng 9 2021
Lời giải:
Theo định lý Bê-du về phép chia đa thức thì để $A(x)$ chia hết cho $x+1$ thì:
$A(-1)=0$
$\Leftrightarrow -a^2+3a+6-2a=0$
$\Leftrightarrow -a^2+a+6=0$
$\Leftrightarrow a^2-a-6=0$
$\Leftrightarrow (a+2)(a-3)=0$
$\Rightarrow a=-2$ hoặc $a=3$
CM
23 tháng 5 2017
Ta có
Phần dư của phép chia trên là R = 6 + a – a 2 . Đề phép chia trên là phép chia hết thì R = 0 ó - a 2 + a + 6 = 0
ó - a 2 – 2a + 3a + 6 = 0
ó -a(a + 2) + 3(a + 2) = 0
ó (a + 2)(-a + 3) = 0 ó a = - 2 a = 3
Vậy có hai giá trị của a thỏa mãn điều kiện đề bài a = -2; a = 3
Đáp án cần chọn là: B
O
0
LT
0
H
12 tháng 12 2018
ĐỂ x4 - x3 + 6x2 -x \(⋮x^2-x+5\)
\(\Rightarrow x-5=0\Rightarrow x=5\)
H
12 tháng 12 2018
b , ta có : \(3x^3+10x^2-5⋮3x+1\)
\(\Rightarrow3x^3+x^2+9x^2+3x-3x-1-4⋮3x+1\)
\(\Rightarrow x\left(3x+1\right)+3x\left(3x+1\right)-\left(3x+1\right)-4⋮3x+1\)
mà : \(\left(3x+1\right)\left(4x-1\right)⋮3x+1\)
\(\Rightarrow4⋮3x+1\Rightarrow3x+1\inƯ\left(4\right)=\left\{\pm1;\pm2;\pm4\right\}\)
Nếu : 3x + 1 = 1 => x = 0 ( TM )
3x + 1 = -1 => x = -2/3 ( loại )
3x + 1 = 2 => x = 1/3 ( loại )
3x + 1 = -2 => x = -1 ( TM )
3x + 1 = 4 => x = 1 ( TM )
3x + 1 = -1 => x = -5/3 ( loại )
\(\Rightarrow x\in\left\{0;\pm1\right\}\)
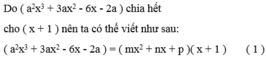
Ta có x + 1 =0
<=> x= -1
Ta có a2x3+3ax2-6x-2a =0
Theo ĐL Bơ_du ta có x= -1 là nghiệm của P(x)
<=> a2( - 1)3 +3a( -1)2 - 6(-1) - 2a =0
<=> -a2 +3a +6 -2a =0
<=> -a(a-3) - 2(a-3) =0
<=> -(a-3)(a+2)=0
<=> (a-3)(a+2)=0
<=> a-3=0 hoặc a+2=0
<=> a=3 hoặc a= -2
Vậy a=3 hoặc a= -2
Để P(x) chia hết cho x+1 thì hệ số số mũ bậc chẵn bằng số mũ bậc lẽ
Nên ta có:\(a^2-6=3a-2\)
\(\Leftrightarrow a^2-3a-4=0\)
\(a=4;-1\)
OKKK