
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a/Áp dụng tính chất của dãy tỉ số bằng nhau, ta có:
\(\dfrac{x}{3}=\dfrac{y}{6}=\dfrac{x+y}{3+6}=\dfrac{90}{9}=10\)
\(\Rightarrow\left\{{}\begin{matrix}x=10\cdot3=30\\y=10\cdot6=60\end{matrix}\right.\)
Vậy ...
b/Ta có:
\(\dfrac{x}{3}=\dfrac{4x}{12}\)
Áp dụng tính chất của dãy tỉ số bằng nhau, ta có:
\(\dfrac{4x}{12}=\dfrac{y}{6}=\dfrac{4x-y}{12-6}=\dfrac{42}{6}=7\)
\(\Rightarrow\left\{{}\begin{matrix}x=7\cdot3=21\\y=7\cdot6=42\end{matrix}\right.\)
Vậy ...
c/Đặt \(x=k;y=k\) ( k \(\in\) N* )
\(\Rightarrow x=3k;=6k\)
Mà \(xy=162\)
\(\Rightarrow3k\cdot6k=162\)
\(\Rightarrow18k^2=162\)
\(\Rightarrow k^2=9\)
\(\Rightarrow k=\pm3\)
\(\Rightarrow\left\{{}\begin{matrix}x=3\cdot3=9\\x=\left(-3\right)\cdot3=-9\\y=3\cdot6=18\\y=\left(-3\right)\cdot6=-18\end{matrix}\right.\)
Vậy ...
#NoSimp

Đặt \(\dfrac{x}{3}=\dfrac{y}{6}=k\Rightarrow x=3k;y=6k\)
\(xy=162\\ \Rightarrow18k^2=162\\ \Rightarrow k^2=9\\ \Rightarrow\left[{}\begin{matrix}k=3\\k=-3\end{matrix}\right.\\ \Rightarrow\left[{}\begin{matrix}x=9;y=18\\x=-9;y=-18\end{matrix}\right.\)
Ta có:\(\dfrac{x}{3}=\dfrac{y}{6}=k\)
\(\Rightarrow\left\{{}\begin{matrix}x=3k\\y=6k\end{matrix}\right.\)
mà \(x.y=162\)
\(\Rightarrow3k.6k=162\)
\(\Rightarrow18k^2=162\)
\(\Rightarrow k=3\)
\(\Rightarrow\left\{{}\begin{matrix}k=3\\k=-3\end{matrix}\right.\)
\(\Rightarrow\left\{{}\begin{matrix}\dfrac{x}{3}=\dfrac{y}{6}=3\\\dfrac{x}{3}=\dfrac{y}{6}=-3\end{matrix}\right.\)
\(\Rightarrow\left\{{}\begin{matrix}x=9;y=18\\x=-9;y=-18\end{matrix}\right.\)


a) Ta có hệ phương trình:
x/8 = y/12
x + y = 60 Giải bằng cách thay x/8 bằng y/12 trong phương trình thứ hai, ta có:
(y/12)*8 + y = 60
2y + y = 60
y = 20 Thay y = 20 vào x + y = 60, ta có x = 40. Vậy kết quả là x = 40, y = 20.
b) Ta có hệ phương trình:
x/3 = y/6
x*y = 162 Thay x/3 bằng y/6 trong phương trình thứ hai, ta có:
y^2 = 324
y = 18 Thay y = 18 vào x/3 = y/6, ta có x = 9. Vậy kết quả là x = 9, y = 18.
c) Ta có hệ phương trình:
x/y = 2/5
xy = 40 Từ phương trình thứ nhất, ta có x = 2y/5. Thay vào xy = 40, ta có:
(2y/5)*y = 40
y^2 = 100
y = 10 Thay y = 10 vào x = 2y/5, ta có x = 4. Vậy kết quả là x = 4, y = 10.
d) Ta có hệ phương trình:
x/7 = y/6
y/8 = z/5
x + y - z = 37 Thay x/7 bằng y/6 trong phương trình thứ ba, ta có x = (7/6)*y - z. Thay y/8 bằng z/5 trong phương trình thứ ba, ta có y = (8/5)*z. Thay x và y vào phương trình thứ ba, ta được:
(7/6)*y - z + y - z = 37
(19/6)*y - 2z = 37 Thay y = (8/5)*z vào phương trình trên, ta có:
(19/6)*(8/5)*z - 2z = 37
z = 30 Thay z = 30 vào y = (8/5)*z, ta có y = 48. Thay y và z vào x/7 = y/6, ta có x = 35. Vậy kết quả là x = 35, y = 48, z = 30.
e) Ta có hệ phương trình:
10x = 15y = 21z
3x - 5z + 7y = 37 Từ phương trình thứ nhất, ta có:
x = 3z/7
y = 3z/5 Thay x và y vào phương trình thứ hai, ta có:
3z/73 - 5z + 73z/5 = 37
3z - 5z + 12z - 245 = 0
10z = 245
z = 24.5 Thay z = 24.5 vào x = 3z/7 và y = 3z/5, ta có x = 10.5 và y = 14.7. Tuy nhiên, kết quả này không phải là một cặp số nguyên. Vậy hệ phương trình không có nghiệm thỏa mãn.

c1: -0,162000>-0,(162)
c2: y=2
c3: y=-10
c4: thêm đk AC=BF

2,Đặt \(\frac{x}{3}=\frac{y}{6}\)\(=k\)
Ta có x=3k; y=6k
Vì x+y=90 nên:3k+6k=90
\(\Leftrightarrow\)k(3+6)=90
9k=90
k=90:9=10
Suy ra k=10\(\hept{\begin{cases}x=3.10=30\\y=6.10=60\end{cases}}\)
3,
Đặt \(\frac{x}{3}=\frac{y}{6}\)\(=k\)
Ta có x=3k; y=6k
Vì 4x-y=42 nên:4.3k-6k=42
\(\Leftrightarrow\) 12k-6k=42
6k=42
k=42:6=7
Suy ra k=7\(\hept{\begin{cases}x=3.7=21\\y=6.7=42\end{cases}}\)
4,
Đặt \(\frac{x}{3}=\frac{y}{6}\)\(=k\)
Ta có x=3k; y=6k
Vì xy=162 nên:3k.6k=162
\(\Leftrightarrow\)k2.18=162
k2=162:18
k2=9
k=\(\pm\)3
Với k=3\(\hept{\begin{cases}x=3.3=9\\y=6.3=18\end{cases}}\)
Với k=-3\(\hept{\begin{cases}x=3.\left(-3\right)=-9\\y=6.\left(-3\right)=-18\end{cases}}\)
5,
Đặt \(\frac{x}{3}=\frac{y}{6}\)\(=k\)
Ta có x=3k; y=6k
Vì 2x2-y2=-8 nên:2.(3k)2-(6k)2=-8
\(\Leftrightarrow\)2.9k2-36k2=-8
18k2-36k2=-8
-18k2=-8
k2=-8/-18=4/9
k=\(\pm\)\(\frac{2}{3}\)
Với k=\(\frac{2}{3}\)\(\hept{\begin{cases}x=\frac{2}{3}.3=2\\y=\frac{2}{3}.6=4\end{cases}}\)
Với k=\(\frac{-2}{3}\)\(\hept{\begin{cases}x=\frac{-2}{3}.3=-2\\y=\frac{-2}{3}.6=-4\end{cases}}\)
6,
Đặt \(\frac{x}{3}=\frac{y}{6}\)\(=k\)
Ta có x=3k; y=6k
Vì x-y=9 nên:3k-6k=9
\(\Leftrightarrow\) -3k=9
k=9:(-3)
k=-3
Suy ra\(\hept{\begin{cases}x=-3.3=-9\\y=-3.6=-18\end{cases}}\)

a)5x+5x+2=650
\(\Rightarrow5^x\left(1+5^2\right)=650\)
\(\Rightarrow5^x\cdot26=650\)
\(\Rightarrow5^x=25\)
\(\Rightarrow5^x=5^2\)
\(\Rightarrow x=2\)
b)\(3^{x-1}+5\cdot3^{x-1}=162\)
\(\Rightarrow3^{x-1}\cdot\left(1+5\right)=162\)
\(\Rightarrow3^{x-1}\cdot6=162\)
\(\Rightarrow3^{x-1}=27\)
\(\Rightarrow3^{x-1}=3^3\)
\(\Rightarrow x-1=3\)
\(\Rightarrow x=4\)
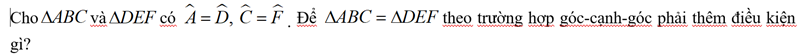
Ta có: \(\dfrac{x}{3}=\dfrac{y}{6}\Rightarrow x=\dfrac{3y}{6}=\dfrac{1}{2}y\)
Theo đề bài ta có : \(xy=162\Rightarrow\dfrac{1}{2}y.y=162\Rightarrow y^2=324\Rightarrow y=18\)
\(\Rightarrow x=\dfrac{1}{2}y=9\)
Đặt \(\dfrac{x}{3}=\dfrac{y}{6}=k\)
\(\Leftrightarrow\left\{{}\begin{matrix}x=3k\\y=6k\end{matrix}\right.\)
Ta có: xy=162
\(\Leftrightarrow18k^2=162\)
\(\Leftrightarrow k^2=9\)
Trường hợp 1: k=3
\(\Leftrightarrow\left\{{}\begin{matrix}x=3k=9\\y=6k=18\end{matrix}\right.\)
Trường hợp 2: k=-3
\(\Leftrightarrow\left\{{}\begin{matrix}x=3k=-9\\y=6k=-18\end{matrix}\right.\)