Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Bài 1:
| GT | \(\widehat{A}+\widehat{B}=90^0;\widehat{C}+\widehat{B}=90^0\) |
| KL | \(\widehat{A}=\widehat{C}\) |
Ta có: \(\widehat{A}+\widehat{B}=90^0\)
nên \(\widehat{A}=90^0-\widehat{B}\left(1\right)\)
Ta có: \(\widehat{C}+\widehat{B}=90^0\)
nên \(\widehat{C}=90^0-\widehat{B}\left(2\right)\)
Từ (1) và (2) suy ra \(\widehat{A}=\widehat{C}\)

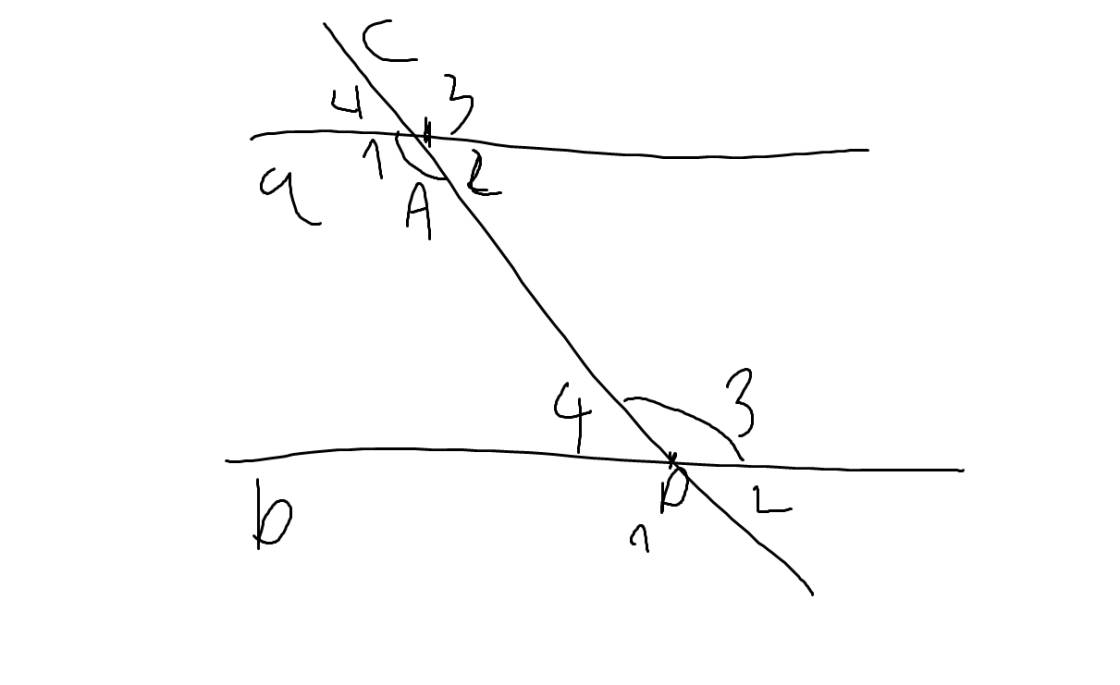
| GT | a cắt c tại A, a cắt b tại D \(\widehat{A_1}=\widehat{D_3}\) |
| KL | \(\widehat{D_3}+\widehat{A_2}=180^0\) |
\(\widehat{A_1}=\widehat{D_3}\)(hai góc so le trong bằng nhau)
mà \(\widehat{A_1}+\widehat{A_2}=180^0\)
nên \(\widehat{A_2}+\widehat{D_3}=180^0\)(ĐPCM)

Chứng minh định lí
A1 + B1 = 1800
Mà A1 + A2 = 1800 ( 2 góc kề bù )
\(\Rightarrow\)B1 = A2
Mà B1 và A2 là 2 góc đồng vị
\(\Rightarrow\)a // b
GT:Nếu hai đg thẳng a,b cất đg thảng c.............bù nhau
KL:Thì a và b song song với nhau

GT:ĐT a,b cắt c tạo thành một cập góc bù nhau
KL:a,b //
chứng minh
ta gọi hai điểm cắt nhau giữa ĐT a,b và c là A,B
Ta có tổng cặp góc trong cùng phía bàng 180 độ
Ta thấy :mỗi cặp góc trong cùng phía đều đối đỉnh với một góc ngoài cùng phía
=>a//b
c a b A B 1 1 2
Chứng minh định lí: Theo đề bài góc A1 + B1 = 180o
Ta có: góc A1 + A2 = 180o (tính chất kề bù)
Góc B1 = A2 mà hai góc này đồng vị => a//b

A B a b c 1 2 1
GT c cắt a tại A c cắt b tại B A2 + B1 = 180 o KL a // b
CM:
\(\widehat{B2}+\widehat{A1}=180^0\) (1)
\(\widehat{B1}+\widehat{B2}=180^0\) ( 2 góc kề bù ) (2)
Từ (1) và (2)
\(\Rightarrow\widehat{B2}+\widehat{A1}=\widehat{B1}+\widehat{B2}\)
\(\Rightarrow\widehat{A1}=\widehat{B1}\) mà 2 góc này ở vị trí đồng vị
\(\Rightarrow a//b\)

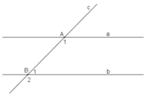
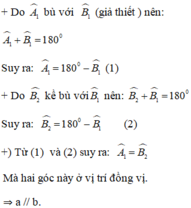
Giả thiết: "Đường thẳng c cắt hai đường thẳng a, b và trong các góc tạo thành có một cặp góc so le trong bằng nhau" ; Kết luận: " Hai góc so le trong còn lại bằng nhau."
Coin Hunter
Chứng minh định lý đâu bạn