Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Ta có :
\(0,25^8==\left(0,5^2\right)^8=0,5^{16}\)
\(0,125^4=\left(0,5^3\right)^4=0,5^{12}\)
\(\begin{array}{l}{\left( {0,25} \right)^8} = {\left[ {{{\left( {0,5} \right)}^2}} \right]^8}=(0,5)^{2.8} = {\left( {0,5} \right)^{16}};\\{\left( {0,125} \right)^4} = {\left[ {{{\left( {0,5} \right)}^3}} \right]^4} =(0,5)^{3.4}= {\left( {0,5} \right)^{12}};\\{\left( {0,0625} \right)^2} = {\left[ {{{\left( {0,5} \right)}^4}} \right]^2} =(0,5)^{4.2}= {\left( {0,5} \right)^8}\end{array}\)
anh có thể viết phân số ra như này ko ạ:
\(\frac{3}{4}\)
viết như vậy em nhìn rối mắt lắm ạ!
chúc b hok tốt
Ta có :
(0,36)8=(0,6.0,6)8=(0,62)8=0,62.8=0,616
(0,216)4=(0,6.0,6.0,6)4=(0,63)4=0,63.4=0,612
Ta có:
\(\left(0,36\right)^8=\left(0,6.0,6\right)^8=\left(0,6^2\right)^8=0,6^{16}\)
\(\left(0,216\right)^4=\left(0,6.0,6.0,6\right)^4=\left(0,6^3\right)^4=0,6^{12}\)
Bài 31 Viết các số%5E%7B8%7D)
và %5E%7B4%7D)
dưới dạng các lũy thừa của cơ số 0,5
Lời giải:
Ta có: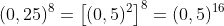
Giải : Ta có:
(0,25)8 =[(0,5)2]8=(0,5)16
(0,125)4=[(0,5)3]4=(0,5)12