Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

\(A\left( { - 2;0} \right)\) \( \Rightarrow \) hoành độ của điểm \(A\) là –2 và tung độ của điểm \(A\) là 0.
\(B\left( {0;4} \right)\) \( \Rightarrow \) hoành độ của điểm \(B\) là 0 và tung độ của điểm \(B\) là 4.
\(C\left( {5;4} \right)\) \( \Rightarrow \) hoành độ của điểm \(C\) là 5 và tung độ của điểm \(C\) là 4.
\(D\left( {3;0} \right)\) \( \Rightarrow \) hoành độ của điểm \(D\) là 3 và tung độ của điểm \(D\) là 0.
Biểu diễn các điểm \(A;B;C;D\) trên mặt phẳng tọa độ ta được:
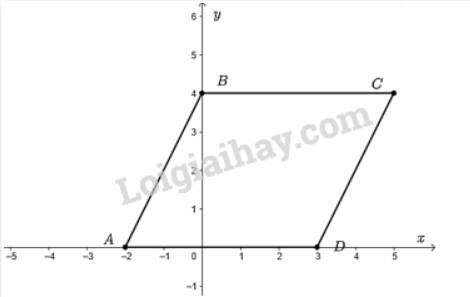
Vì hai điểm \(B;C\) có tung độ bằng nhau nên \(BC\) song song với \(Ox\); Hai điểm \(A;D\) có tung độ bằng nhau nên \(AD\) song song với \(Ox\).
Do đó, \(BC//AD\).
Lại có, \(AD = \left| {3 - \left( { - 1} \right)} \right| = 4;BC = \left| {4 - 0} \right| = 4\). Do đó, \(AD = BC\).
Xét tứ giác \(ABCD\)có:
\(AD = BC\)
\(BC//AD\)
Do đó, tứ giác \(ABCD\) là hình bình hành.

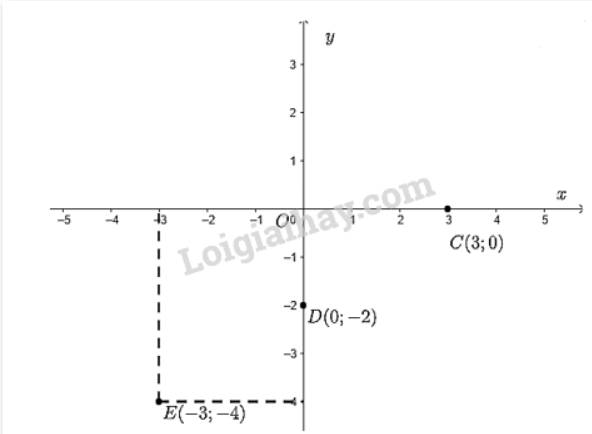
- Đánh dấu điểm \(C\left( {3;0} \right)\)
Từ điểm 3 trên trục hoành ta vẽ đường thẳng vuông góc với \(Ox\); Từ điểm 0 trên trục tung ta vẽ đường thẳng vuông góc với \(Oy\) (chính là trục \(Ox\)). Giao điểm của hai đường thẳng này chính là điểm \(C\left( {3;0} \right)\);
- Đánh dấu điểm \(D\left( {0; - 2} \right)\)
Từ điểm 0 trên trục hoành ta vẽ đường thẳng vuông góc với \(Ox\)(chính là trục \(Oy\)); Từ điểm -2 trên trục tung ta vẽ đường thẳng vuông góc với \(Oy\). Giao điểm của hai đường thẳng này chính là điểm \(D\left( {0; - 2} \right)\).
- Đánh dấu điểm \(E\left( { - 3; - 4} \right)\)
Từ điểm -3 trên trục hoành ta vẽ đường thẳng vuông góc với \(Ox\); Từ điểm -4 trên trục tung ta vẽ đường thẳng vuông góc với \(Oy\). Giao điểm của hai đường thẳng này chính là điểm \(E\left( { - 3; - 4} \right)\).
Ta có hình vẽ

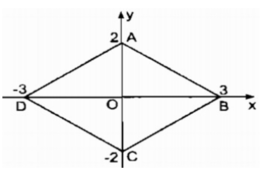
Ta có: A(0;2) và C(0;-2) là hai điểm đối xứng qua O(0;0)
⇒ OA = OC
B(3;0) và D(-3; 0) là hai điểm đối xứng qua O(0;0)
⇒ OB = OD
Tứ giác ABCD là hình bình hành (vì có hai đường chéo cắt nhau tại trung điểm của mỗi đường)
Lại có: Ox ⊥ Oy hay AC ⊥ BD.
Vậy tứ giác ABCD là hình thoi
Trong ∆ OAB vuông tại O, theo định lý Pi-ta-go ta có:
A B 2 = O A 2 + O B 2
A B 2 = 2 2 + 3 2 = 4 + 9 = 13
AB = 13
Vậy chu vi của hình thoi bằng 4 13

Bạn nhập lại hai hàm số đó nhé chính giữa mik không biết là dấu + hay -

a)
Điểm \(A\left( { - 2;0} \right) \Rightarrow \) hoành độ là -2 và tung độ là 0.
Điểm \(B\left( {3;0} \right) \Rightarrow \) hoành độ là 3 và tung độ là 0.
Điểm \(C\left( {4;0} \right) \Rightarrow \) hoành độ là 4 và tung độ là 0.
Biểu diễn ba điểm \(A;B;C\) trên hệ trục tọa độ ta được
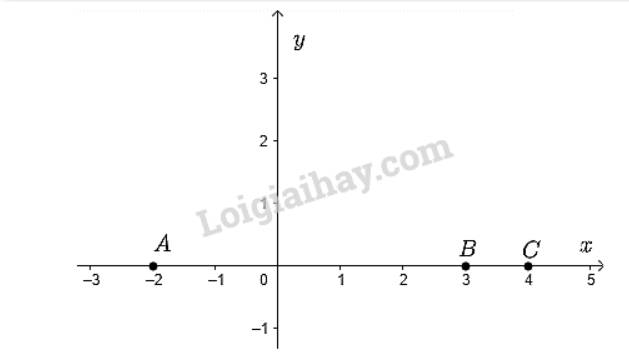
Nhận xét: Cả ba điểm \(A;B;C\) đều nằm trên trục hoành.
b) Từ ví dụ ở câu a ta thấy tất cả các điểm nằm trên trục hoành đều có tung độ bằng 0.

a) Xét ΔABC vuông tại A có \(\widehat{C}=30^0\)(gt)
mà cạnh đối diện với \(\widehat{C}\)
nên \(\dfrac{AB}{BC}=\dfrac{1}{2}\)(Định lí)
Xét ΔABC có BD là đường phân giác ứng với cạnh AC(gt)
nên \(\dfrac{AD}{CD}=\dfrac{AB}{BC}\)(Tính chất tia phân giác của tam giác)
hay \(\dfrac{AD}{CD}=\dfrac{1}{2}\)
b) Ta có: \(BC=2\cdot AB\)(cmt)
nên \(BC=2\cdot12.5=25\left(cm\right)\)
Áp dụng định lí Pytago vào ΔBAC vuông tại A, ta được:
\(BC^2=AB^2+AC^2\)
\(\Leftrightarrow AC^2=BC^2-AB^2=25^2-12.5^2=468.75\)
hay \(AC=\dfrac{25\sqrt{3}}{2}cm\)
Diện tích tam giác ABC là:
\(S_{ABC}=\dfrac{AB\cdot AC}{2}=\dfrac{12\cdot\dfrac{25\sqrt{3}}{2}}{2}=\dfrac{150\sqrt{3}}{2}=75\sqrt{3}\left(cm^2\right)\)

a) Xét tam giác ABC vuông tại A có:
* \(BC^2=AB^2+AC^2\)(định lý Py-ta-go)
\(< =>10^2=6^2+AC^2\)
\(< =>AC^2=100-36\)
\(< =>AC=\sqrt{64}\)
\(< =>AC=8\)
Chu vi tam giác ABC là : \(AB+AC+BC=6+10+8=24\left(cm\right)\)
Diện tích tam giác ABC là: \(\frac{AB.AC}{2}=\frac{6.8}{2}=24\left(cm^2\right)\)
b) Ta có: BD là phân giác của góc B (gt)
=> \(\frac{DA}{DC}=\frac{BA}{BC}\)(tính chất đường phân giác trong 1 tam giác)
Mà \(\frac{BA}{BC}=\frac{6}{10}=\frac{3}{5}\)
=>\(\frac{DA}{DC}=\frac{3}{5}\)
c) Xét tam giác ABI có:
* BD là phân giác góc B (gt)
* BD là đường cao (AI vuông góc BD)
=> Tam gi1c ABI cân tại B
=> BA = BI (tính chất)
Xét tam giác ABD và tam giác IBD có:
*AB = IB (cmt)
*Góc ABD = Góc IBD (BD là phân giác)
*BD là cạnh chung
=> tam giác ABD = tam giác IBD (c-g-c)
=> Góc BAD = Góc BID (tính chất)
Mà góc BAD = 90 độ (tam giác ABC vuông tại A)
=> Góc BID = 90 độ

a: A(0;4); B(-3;0); C(3;0)
\(AB=\sqrt{\left(-3-0\right)^2+\left(0-4\right)^2}=5\)
\(AC=\sqrt{\left(3-0\right)^2+\left(0-4\right)^2}=5\)
\(BC=\sqrt{\left(3+3\right)^2+\left(0-0\right)^2}=6\)
Chu vi tam giác ABC là:
5+5+6=16
Xét ΔABC có \(cosBAC=\dfrac{AB^2+AC^2-BC^2}{2\cdot AB\cdot AC}=\dfrac{5^2+5^2-6^2}{2\cdot5\cdot5}=\dfrac{7}{25}\)
=>\(sinBAC=\sqrt{1-\left(\dfrac{7}{25}\right)^2}=\dfrac{24}{25}\)
Diện tích tam giác ABC là:
\(S_{ABC}=\dfrac{1}{2}\cdot AB\cdot AC\cdot sinBAC\)
\(\dfrac{1}{2}\cdot5\cdot5\cdot\dfrac{24}{25}=\dfrac{24}{2}=12\)
b: Khoảng cách từ C đến AB là:
\(2\cdot\dfrac{S_{ABC}}{AB}=\dfrac{2\cdot12}{5}=\dfrac{24}{5}=4,8\)
Xin cảm ơn ạ.