Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

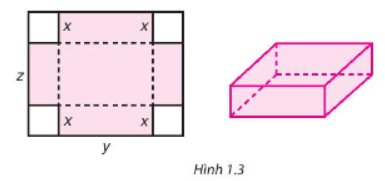
Hình gấp được là hình hộp chữ nhật có:
Chiều rộng là \(z - 2x\) (centimet)
Chiều dài là \(y - 2x\) (centimet)
Chiều cao là \(x\) (centimet)
Thể tích chiếc hộp là: \(\left( {z - 2x} \right).\left( {y - 2x} \right).x = \left( {zy - 2xz - 2xy + 4{x^2}} \right).x = xyz - 2{x^2}z - 2{x^2}y + 4{x^3}\) ( centimet khối)
Đa thức này có bậc là 3.

a) Diện tích miếng tôn ban đầu = ( x + 2 )( x + 2 ) = x2 + 4x + 4
Diện tích miếng tôn mà bác thợ cắt = ( x - 3 )( x - 3 ) = x2 - 6x + 9
=> Diện tích miếng tôn còn lại = x2 + 4x + 4 - ( x2 - 6x + 9 ) = x2 + 4x + 4 - x2 + 6x - 9 = 10x - 5
b) Với x = 7 => Diện tích miếng tôn còn lại = 10.7 - 5 = 70 - 5 = 65(cm)

Cắt một hình thoi theo đường kẻ xanh như hình vẽ trên, ta được 4 tam giác bằng nhau. Ghép 4 tam giác vào 4 góc của hình thoi còn lại như sau để được hình chữ nhật:
- Nhận xét:
+ Diện tích hình chữ nhật = 2 lần diện tích hình thoi
+ Hình chữ nhật có chiều dài và chiều rộng là 2 đường chéo của hìn thoi
=> Diện tích hình thoi = Diện tích hình chữ nhật : 2 = Tích 2 đường chéo của hình thoi : 2

3\(a^2\)+4a+1=3\(a^2\)+3a+a+1
=(3\(a^2\)+3a)+(a+1)
=3a(a+1)+(a+1)
=(a+1)(3a+1)

S A B x x x x 20 cm
Mình vẽ hơi xấu nên nó k bằng nhau ^_^
a) ta thấy chiều dài của hcn B là cạnh của đáy S
Cạnh đầu tiên của đáy là 20 - 2x
Ta thấy chiều dài của hcn A là cạnh của đáy S
Cạnh thứ hai của đáy là 20 - 2x
Vậy Diện tích đáy S là (20 - 2x)2
b) khi gấp lại thành hình hộp chữ nhật thì x cũng là chiều cao của hình nên
Thể tích HHCN là x(20 - 2x)2

Gọi x (cm) là độ dài cạnh AC (x > 2).
Gọi hình chữ nhật là MNPA như hình vẽ.
Ta có: MC = AC – AM = x – 2 (cm)
Vì MN // AB nên theo định lý Talet ta có tỉ lệ:
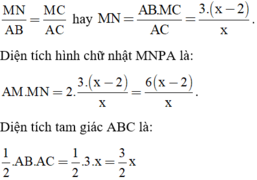
Vì diện tích tam giác ABC gấp đôi diện tích hình chữ nhật MNPA nên ta có phương trình:
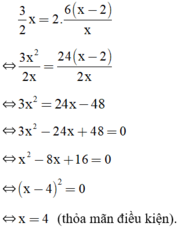
Vậy độ dài đoạn thẳng AC là 4cm.
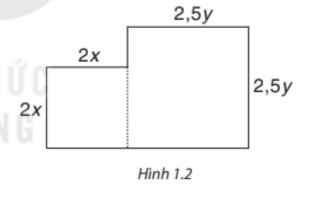

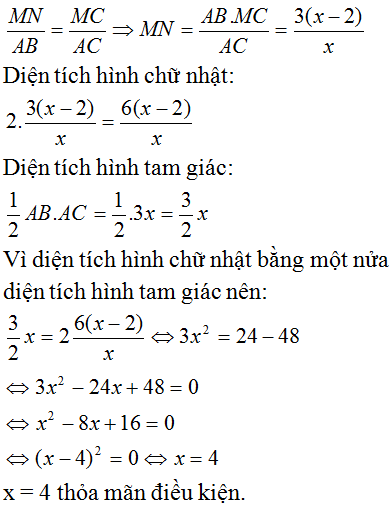
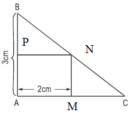
Diện tích hai hình vuông là: \(2x.2x + 2,5y.2,5y = 4{x^2} + 6.25{y^2}\)
Diện tích hai hình tròn là: \({\pi .{x^2} + \pi .{y^2}}\)
Diện tích phần còn lại của miếng bìa là:
\(\begin{array}{l}S = 4{x^2} + 6.25{y^2} - \pi .{x^2} - \pi .{y^2}\\ = \left( {4 - \pi } \right){x^2} + \left( {6,25 - \pi } \right){y^2}\end{array}\)
Biểu thức này là một đa thức, có bậc là 2.