Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Tham khảo: Đường truyền của ba tia sáng đặc biệt qua thấu kính hội tụ: (1): Tia tới đến quang tâm thì tia ló tiếp tục truyền thẳng theo phương của tia tới. (2): Tia tới song song với trục chính thì tia ló qua tiêu điểm. (3): Tia tới qua tiêu điểm thì tia ló song song với trục chính.

a)Bạn tự vẽ hình nha!!!
b)Khoảng cách từ ảnh đến thấu kính:
\(\dfrac{1}{f}=\dfrac{1}{d}+\dfrac{1}{d'}\Rightarrow\dfrac{1}{10}=\dfrac{1}{40}+\dfrac{1}{d'}\)
\(\Rightarrow d'=\dfrac{40}{3}\approx13,33cm\)
Độ cao ảnh: \(\dfrac{h}{h'}=\dfrac{d}{d'}\Rightarrow\dfrac{h}{h'}=\dfrac{40}{\dfrac{40}{3}}=3\)
Vậy vật lớn hơn ảnh và lớn gấp 3 lần.

b) Xét \(\Delta ABO\sim\Delta A'B'O\left(g.g\right)\)
\(\Rightarrow\dfrac{AB}{A'B'}=\dfrac{AO}{A'O}\Leftrightarrow\dfrac{h}{h'}=\dfrac{d}{d'}\left(1\right)\)
Xét \(\Delta IOF'\sim\Delta B'A'F'\left(g.g\right)\)
\(\Rightarrow\dfrac{IO}{A'B'}=\dfrac{OF}{A'O}\Leftrightarrow\dfrac{AB}{A'B'}=\dfrac{OF}{OA'-OF'}\Leftrightarrow\dfrac{h}{h'}=\dfrac{f}{d'-f}\left(2\right)\)
Từ (1) và (2) \(\Rightarrow\dfrac{d}{d'}=\dfrac{f}{d'-f}\Leftrightarrow\dfrac{18}{d'}=\dfrac{12}{d'-12}\Leftrightarrow5d'-60=48\Leftrightarrow d'=36\left(cm\right)\)

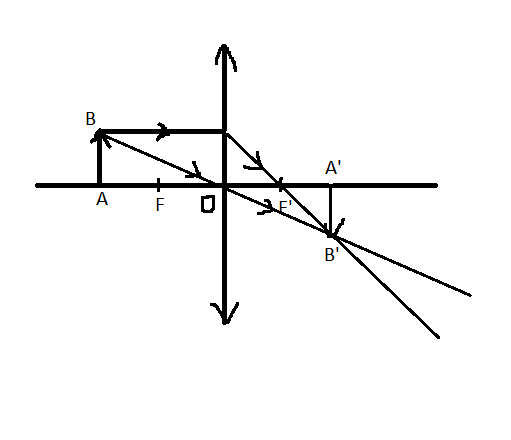
Khoảng cách từ ảnh đến thấu kính:
\(\dfrac{1}{f}=\dfrac{1}{d}+\dfrac{1}{d'}\Rightarrow\dfrac{1}{12}=\dfrac{1}{20}+\dfrac{1}{d'}\Rightarrow d'=30cm\)

Nếu làm ra thì dài nên mik chỉ bạn cách làm nha
Trường hợp vật cách TKHT 8cm
=> vật nằm trong khoảng tiêu cự
dùng công thức \(\dfrac{h'}{h}=\dfrac{d'}{d};\dfrac{1}{d}-\dfrac{1}{d'}=\dfrac{1}{f}\)
Trường hợp vật cách TKHT 16cm, 24cm, 36cm
=> vật nằm ngoài khoảng tiêu cự
dùng công thức \(\dfrac{h'}{h}=\dfrac{d'}{d};\dfrac{1}{d}+\dfrac{1}{d'}=\dfrac{1}{f}\)
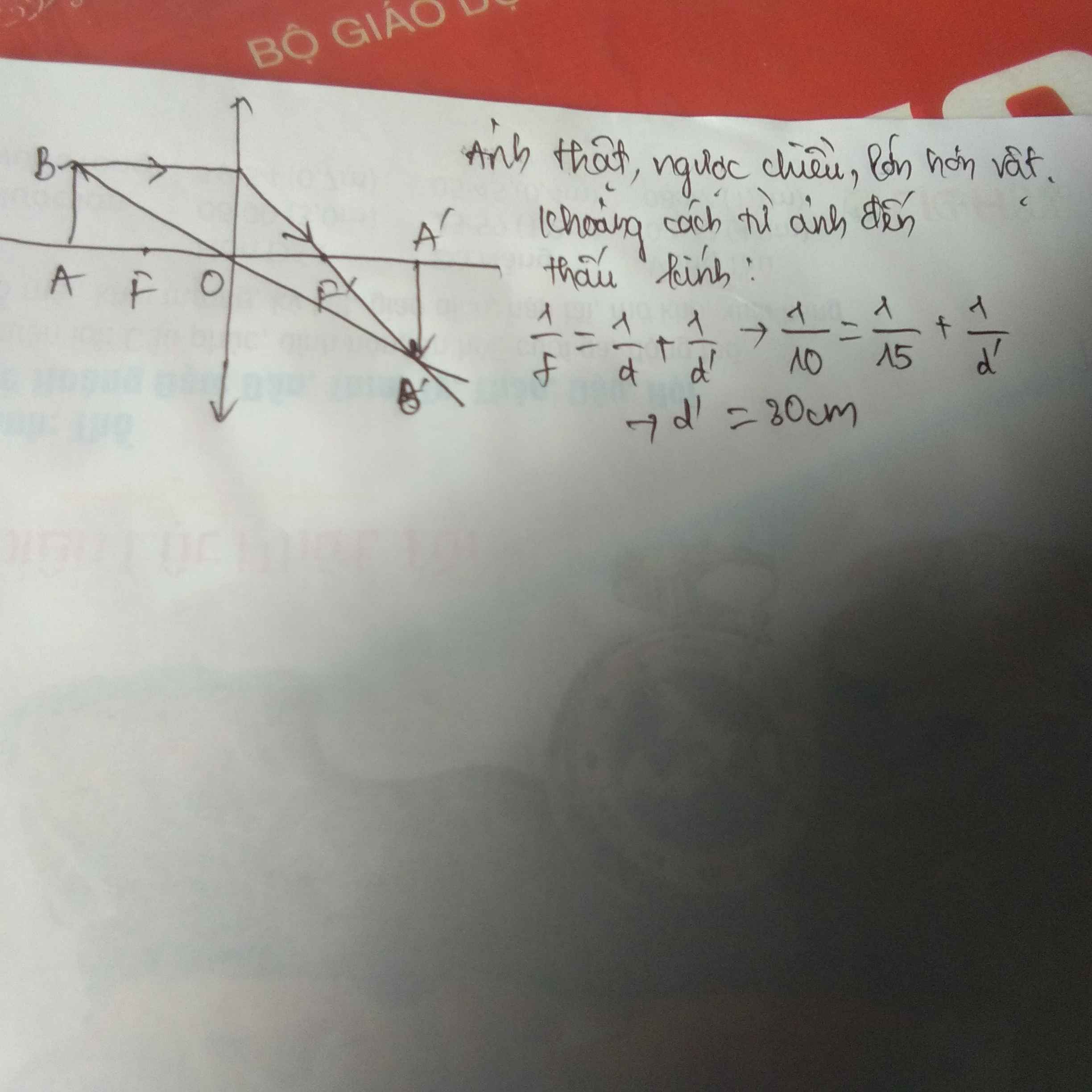
Tham khảo :v