Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Vị trí hai vân sáng trùng nhau thỏa mãn
\(k_1 i_1 = k_2 i_2 \)
<=> \(k_1 \lambda_1 = k_2 \lambda_2\)
<=> \(\frac{k_1}{k_2}= \frac{\lambda_2}{\lambda_1} = \frac{660}{500}= \frac{33}{25}.\)(*)
Vị trí hai vân sáng trùng nhau đầu tiên (trừ vân trung tâm) ứng với \(k_1;k_2\) nhỏ nhất thỏa mãn (*) tức là \(k_1 = 33; k_2 = 25.\)
Thay \(k_1 =33=> \Delta x_{min}= 33.\frac{500.10^{-3}.1,2}{2}=9,9mm.\)
Với \(\lambda = 500nm = 500,10^{-3}\mu m; a = 2mm; D = 1,2m.\)

Chọn D
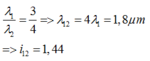
Trong khoảng đó (kể cả 2 đầu) có 5 vân của λ1, 4 vân của λ2, trừ đi 2 vân 2 đầu tính 2 lần => có 7 vân

Phương pháp:
Sử dụng lí thuyết về bài toán trùng nhau của 2 bức xạ trong giao thoa sóng ánh sáng
Hai bức xạ trùng nhau: x1 = x2 <=> k1.λ1 = k2.λ2
Cách giải:
+ Ta có: i1 = 0,6 mm và i2 = 0,78 mm
+ Vị trí hai bức xạ trùng nhau:
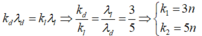

+ Số vân sáng của λ 1 = 500 nm trên đoạn MN là:
![]()
có 10 giá trị
+ Số vân sáng của λ 2 = 650 nm trên đoạn MN là:
![]()
có 8 giá trị
+ Số vân sáng trùng của hai bức xạ trên đoạn MN là:
![]()
có 1 giá trị
+ Số vân sáng quan sát được là: N = N1 + N2 – N0 = 17
Chọn B

\(i =\frac{\lambda D}{a}= \frac{0,6.1,5}{0,5}= 1,8mm.\)
Nhận xét
\(\frac{x_M}{i}=3 \in Z\)=> M là vân sáng bậc 3.

- Điều kiện để cho vân sáng tại vị trí M của bức xạ đơn sắc:
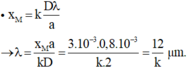
- Với khoảng giá trị của bước sóng 0,38 µm ≤ λ ≤0,76 µm. Sử dụng chức năng Mode → 7 ta tìm được tại M có hai bức xạ đơn sắc cho vân sáng ứng với:
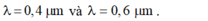

Đáp án B
+ Điều kiện để cho vân sáng tại vị trí M của bức xạ đơn sắc:
![]()
+ Với khoảng giá trị của bước sóng
![]() .
.
Sử dụng chức năng Mode ![]() 7 ta tìm được tại M có hai bức xạ đơn sắc cho vân sáng ứng với
7 ta tìm được tại M có hai bức xạ đơn sắc cho vân sáng ứng với ![]() và
và ![]() .
.
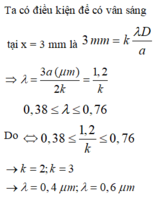
Vân trung tâm trùng nhau Vân trùng = k1i1 = k2i2
Gọi \(x_T\) là khoảng cách từ vân chính giữa đến vân cùng màu gần nó nhất (hai vân trùng nhau gần nhất).
Vì tại vị trí trùng nhau đều có bức xạ của 2 vân nên: \(x_T=k_1i_1=k_2i_2\)(\(k_1,k_2\) tối giản).
\(\Rightarrow k_1\frac{\lambda_1D}{a}=k_2\frac{\lambda_2D}{a}\Rightarrow k_1\lambda_1=k_2\lambda_2\)
\(\Rightarrow\frac{k_1}{k_2}=\frac{\lambda_2}{\lambda_1}=\frac{660}{500}=\frac{33}{25}\)
\(\Rightarrow\begin{cases}k_1=33\\k_2=25\end{cases}\)
Vậy \(x_T=k_1i_1=33.\frac{0,5.1,2}{2}=9,9mm\)
Đáp án C.