Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a:
Theo đề, ta có:
\(\left\{{}\begin{matrix}x_B+x_C=-8\\x_C+x_A=4\\x_B+x_A=4\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x_B+x_C=-8\\x_C-x_B=0\\x_A+x_B=4\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x_C=-4\\x_B=-4\\x_A=4-x_B=4-\left(-4\right)=8\end{matrix}\right.\)
Theo đề, ta có:
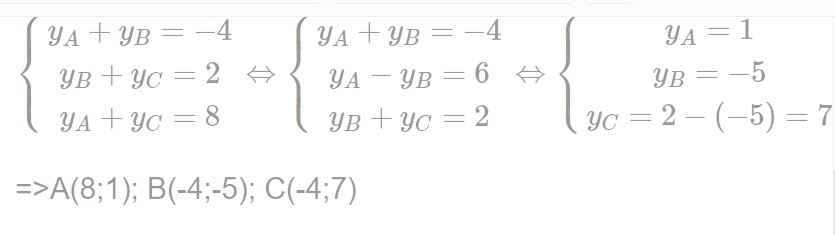
b: Tọa độ trọng tâm của tam giác MNP là:
\(\left\{{}\begin{matrix}x=\dfrac{-4+2+2}{3}=0\\y=\dfrac{1+4-2}{3}=1\end{matrix}\right.\)
A(8;1); B(-4;-5); C(-4;7)
Vì 0=(8-4-4)/3 và 1=(1-5+7)/3
nên ΔBAC và ΔMNP có cùng trọng tâm

A B C A' B' C' a)Do A',B',C' là trung điểm BC,CA,AB=> A'B' song song với AB,B'C'song song với BC,C'A' song song với CA
\(\overrightarrow{A'B'}=\left(6;3\right)\) => VTPT của đường thẳng AB là: \(\overrightarrow{n}=\left(1;-2\right)\)
và C' thuộc (AB)=>Phương trình đường thẳng AB là:
(AB): x-2y-6=0
Tương tự ta có phương trình đường thẳng BC là:
(BC): x+4=0
Tọa độ điểm B là nghiệm hệ
\(\left\{{}\begin{matrix}\text{x-2y-6=0}\\x+4=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=-4\\y=-5\end{matrix}\right.\)
=>B(-4;-5)
A'(-4;1) là TĐ của BC => tọa độ C(-4;7)
C'(2;-2) là TĐ của AB =>tọa độ A(8;1)
b) Gọi tọa độ trọng tâm G của tam giác A'B'C' là G(x;y)
=>\(\overrightarrow{GA'}+\overrightarrow{GB'}+\overrightarrow{GC'}=0\)
=>\(\left\{{}\begin{matrix}\left(-4-x\right)+\left(2-x\right)+\left(2-x\right)=0\\\left(1-y\right)+\left(4-y\right)+\left(-2-y\right)=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=0\\y=1\end{matrix}\right.\)
=>G(0;1)
Thay vào tính
Ta có:\(\overrightarrow{GA}+\overrightarrow{GB}+\overrightarrow{GC}\) =(8-4-4;1-1+7-1-5-1)=(0;0)
=>G là trọng tâm tam giác ABC=>ĐPCM

a) Do M, N, P là trung điểm của các cạnh BC, CA, AB nên:
\(\left\{ \begin{array}{l}\frac{{{x_B} + {x_C}}}{2} = {x_M}\\\frac{{{x_B} + {x_A}}}{2} = {x_P}\\\frac{{{x_A} + {x_C}}}{2} = {x_N}\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}{x_B} + {x_C} = 4\\{x_B} + {x_A} = 2\\{x_A} + {x_C} = 8\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}{x_A} = 3\\{x_B} = - 1\\{x_C} = 5\end{array} \right.\) và \(\left\{ \begin{array}{l}\frac{{{y_B} + {y_C}}}{2} = {y_M}\\\frac{{{y_B} + {y_A}}}{2} = {y_P}\\\frac{{{y_A} + {y_C}}}{2} = {y_N}\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}{y_B} + {y_C} = 0\\{y_B} + {y_A} = 4\\{y_A} + {y_C} = 6\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}{y_A} = 5\\{y_B} = - 1\\{y_C} = 1\end{array} \right.\)
Vậy \(A\left( {3;5} \right),B\left( { - 1; - 1} \right),C\left( {5;1} \right)\)
b) Trọng tâm tam giác ABC có tọa độ là: \(\left\{ \begin{array}{l}\frac{{{x_A} + {x_B} + {x_C}}}{3} = \frac{{3 + \left( { - 1} \right) + 5}}{3} = \frac{7}{3}\\\frac{{{y_A} + {y_B} + {y_C}}}{3} = \frac{{5 + \left( { - 1} \right) + 1}}{3} = \frac{5}{3}\end{array} \right.\)
Trọng tâm tam giác MNP có tọa độ là: \(\left\{ \begin{array}{l}\frac{{{x_M} + {x_N} + {x_P}}}{3} = \frac{{2 + 4 + 1}}{3} = \frac{7}{3}\\\frac{{{y_M} + {y_N} + {y_P}}}{3} = \frac{{0 + 2 + 3}}{3} = \frac{5}{3}\end{array} \right.\)
Vậy trọng tâm của 2 tam giác ABC và MNP là trùng nhau vì có cùng tọa độ.

Tọa độ G là;
\(\left\{{}\begin{matrix}x=\dfrac{4+2+0}{3}=2\\y=\dfrac{0-4-2}{3}=-2\end{matrix}\right.\)
Tọa độ M là:
x=(2+0)/2=1 và y=(-4-2)/2=-3
Tọa độ N là:
x=(4+0)/2=2 và y=(0-2)/2=-1
Tọa độ P là;
x=(4+2)/2=3 và y=(0-4)/2=-2
Tọa độ trọng tâm của tam giác MNP là:
\(\left\{{}\begin{matrix}x=\dfrac{1+2+3}{3}=2\\y=\dfrac{-3-1-2}{3}=-2\end{matrix}\right.\)
=>Tam giác ABC và tam giác MNP có chung trọng tâm

Câu 1:
a: Vì I thuộc trục Ox nên I(x;0)
\(\overrightarrow{AI}=\left(x+1;-1\right)\)
\(\overrightarrow{AB}=\left(1;2\right)\)
Vì A,I,B thẳng hàng nên \(\dfrac{x+1}{1}=-\dfrac{1}{2}\)
=>x=-3/2
b: \(\overrightarrow{AM}=\left(m+5;2m\right)\)
Vì A,M,B thẳng hàng nên \(\dfrac{m+5}{1}=\dfrac{2m}{2}\)
=>m+5=m(vô lý)

1/ M là TĐ của BC=> \(\left\{{}\begin{matrix}x_M=\frac{x_B+x_C}{2}\\y_M=\frac{y_B+y_C}{2}\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x_B+x_C=2\\y_B+y_C=-2\end{matrix}\right.\)
Tương tự \(\left\{{}\begin{matrix}x_C+x_A=6\\y_C+y_A=4\end{matrix}\right.;\left\{{}\begin{matrix}x_A+x_B=0\\y_A+y_B=-10\end{matrix}\right.\)
Tự kết hợp các hpt vs để tìm nhoa, bởi đến đây là siu ez rùi đoá :)
2/ \(\left\{{}\begin{matrix}x_G=\frac{x_A+x_B+x_C}{3}\\y_G=\frac{y_A+y_B+y_C}{3}\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}2=\frac{1+x_B-2}{3}\\1=\frac{3+y_B+4}{3}\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x_B=7\\y_B=-4\end{matrix}\right.\Rightarrow B\left(7;-4\right)\)
3/ \(\left\{{}\begin{matrix}x_C=\frac{x_A+x_B+x_D}{3}\\y_C=\frac{y_A+y_B+y_D}{3}\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}2=\frac{-4+2+x_D}{3}\\-2=\frac{1+4+y_D}{3}\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x_D=8\\y_D=-11\end{matrix}\right.\Rightarrow D\left(8;-11\right)\)

a) Gọi tọa độ các điểm như sau: \(A\left( {{x_A};{y_A}} \right),B\left( {{x_B};{y_B}} \right),C\left( {{x_C};{y_C}} \right)\)
\(M\left( {2;2} \right),N\left( {3;4} \right),P\left( {5;3} \right)\) lần lượt là trung điểm của các cạnh AB, BC và CA nên ta có:
\(\left\{ \begin{array}{l}{x_A} + {x_B} = 2{x_M}=4\\{x_A} + {x_C} = 2{x_P}=10\\{x_C} + {x_B} = 2{x_N}=6\\{y_A} + {y_B} = 2{y_M}=4\\{y_A} + {y_C} = 2{y_P}=8\\{y_C} + {y_B} = 2{y_N}=6\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}{x_A} + {x_B} = 4\\{x_C} - {x_B} = 6\\{x_C} + {x_B} = 6\\{y_A} + {y_B} = 4\\{y_C} - {y_B} = 4\\{y_C} + {y_B} = 6\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}{x_A} = 4\\{x_B} = 0\\{x_C} = 6\\{y_A} = 3\\{y_B} = 1\\{y_C} = 5\end{array} \right.\)
Vậy các đỉnh của tam giác có tọa độ là \(A\left( {4;3} \right),B\left( {0;1} \right),C\left( {6;5} \right)\)
b) Gọi \(G\left( {{x_G};{y_G}} \right),G'\left( {{x_{G'}};{y_{G'}}} \right)\) là trọng tâm của hai tam giác ABC và MNP
Áp dụng tính chất trọng tâm ta có:
\(\begin{array}{l}{x_G} = \frac{{{x_A} + {x_B} + {x_C}}}{3} = \frac{{4 + 0 + 6}}{3} = \frac{{10}}{3};{y_G} = \frac{{{y_A} + {y_B} + {y_C}}}{3} = \frac{{3 + 1 + 5}}{3} = 3\\{x_{G'}} = \frac{{{x_M} + {x_N} + {x_P}}}{3} = \frac{{2 + 3 + 5}}{3} = \frac{{10}}{3};{y_{G'}} = \frac{{{y_M} + {y_N} + {y_P}}}{3} = \frac{{2 + 4 + 3}}{3} = 3\end{array}\)
Suy ra \(G\left( {\frac{{10}}{3};3} \right)\) và \(G'\left( {\frac{{10}}{3};3} \right)\), tọa độ của chúng bằng nhau nên hai điểm G và G’ trùng nhau (đpcm)
c) Ta có: \(\overrightarrow {AB} = \left( { - 4; - 2} \right),\overrightarrow {AC} = \left( {2;2} \right),\overrightarrow {BC} = \left( {6;4} \right)\)
Suy ra: \(AB = \left| {\overrightarrow {AB} } \right| = \sqrt {{{( - 4)}^2} + {{( - 2)}^2}} = 2\sqrt 5 ,AC = \left| {\overrightarrow {AC} } \right| = \sqrt {{2^2} + {2^2}} = 2\sqrt 2 \)
\(BC = \left| {\overrightarrow {BC} } \right| = \sqrt {{6^2} + {4^2}} = 2\sqrt {13} \)
\(\begin{array}{l}\cos A = \cos \left( {\overrightarrow {AB} ,\overrightarrow {AC} } \right) = \frac{{\overrightarrow {AB} .\overrightarrow {AC} }}{{AB.AC}} = \frac{{( - 4).2 + ( - 2).2}}{{2\sqrt 5 .2\sqrt 2 }} = - \frac{{3\sqrt {10} }}{{10}} \Rightarrow \widehat A \approx 161^\circ 33'\\\cos B = \cos \left( {\overrightarrow {BA} ,\overrightarrow {BC} } \right) = \frac{{\overrightarrow {BA} .\overrightarrow {BC} }}{{BA.BC}} = \frac{{4.6 + 2.4}}{{2\sqrt 5 .2\sqrt {13} }} = \frac{{8\sqrt {65} }}{{65}} \Rightarrow \widehat B = 7^\circ 7'\\\widehat C = 180^\circ - \widehat A - \widehat B = 180^\circ - 161^\circ 33' - 7^\circ 7' = 11^\circ 20'\end{array}\)

Theo tích chất đường trung bình trong một tam giác ta có: \(\overrightarrow {PN} = \overrightarrow {BM} = \overrightarrow {MC} \) và \(\overrightarrow {MP} = \overrightarrow {NA} \)
Gọi \(A\left( {{a_1},{a_2}} \right),B\left( {{b_1};{b_2}} \right),C\left( {{c_1};{c_2}} \right)\)
Ta có: \(\overrightarrow {PN} = \left( {2;3} \right)\),\(\overrightarrow {BM} = \left( {1 - {b_1}; - 2 - {b_2}} \right)\), \(\overrightarrow {MC} = \left( {{c_1} - 1;{c_2} + 2} \right)\), \(\overrightarrow {MP} = \left( {5;4} \right)\), \(\overrightarrow {NA} = \left( {{a_1} - 4;{a_2} + 1} \right)\)
Có \(\overrightarrow {PN} = \overrightarrow {BM} \Leftrightarrow \left\{ \begin{array}{l}2 = 1 - {b_1}\\3 = - 2 - {b_2}\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}{b_1} = - 1\\{b_2} = - 5\end{array} \right.\) .Vậy \(B\left( { - 1; - 5} \right)\)
Có \(\overrightarrow {PN} = \overrightarrow {MC} \Leftrightarrow \left\{ \begin{array}{l}2 = {c_1} - 1\\3 = {c_2} + 2\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}{c_1} = 3\\{c_2} = 1\end{array} \right.\) .Vậy \(C\left( {3;1} \right)\)
Có \(\overrightarrow {NA} = \overrightarrow {MP} \Leftrightarrow \left\{ \begin{array}{l}5 = {a_1} - 4\\4 = {a_2} + 1\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}{a_1} = 9\\{a_2} = 3\end{array} \right.\) .Vậy \(A\left( {9;3} \right)\)