Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

\(AB\left\{{}\begin{matrix}quaA\left(-1;-3\right)\\VTCP\overrightarrow{AB}=\left(-2;8\right)\end{matrix}\right.\)
\(PTTS\) của \(AB:\left\{{}\begin{matrix}x=-1-2t\\y=-3+8t\end{matrix}\right.\)
Gọi \(I\left(x_I;y_I\right)\) là tâm đường tròn
\(I\) là trung điểm \(AB\)
\(\left\{{}\begin{matrix}x_I=\dfrac{x_A+x_B}{2}=\dfrac{-1-3}{2}=-2\\y_I=\dfrac{y_A+y_B}{2}=\dfrac{-3+5}{2}=1\end{matrix}\right.\)
\(\Rightarrow I\left(-2;1\right)\)
\(AB=\sqrt{\left(-2\right)^2+8^2}=2\sqrt{17}\)
Mà \(R=\dfrac{AB}{2}=\dfrac{2\sqrt{17}}{2}=\sqrt{17}\)
Vậy \(PT\left(C\right):\left(x+2\right)^2+\left(y-1\right)^2=17\)

`|AB| = \sqrt((1-3)^2+(-2-4)^2)=2\sqrt10`
`=>` PT: `(x-1)^2+(y+2)^2=40`

a) Viết phương trình tổng quát của AB và tính diện tích tam giác ABC
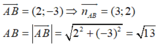
Phương trình tổng quát của AB là: 3(x - 1) + 2(y - 2) = 0 ⇔ 3x + 2y - 7 = 0
Kẻ CH ⊥ AB, (H ∈ AB)
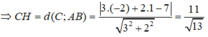
Diện tích tam giác ABC là:
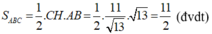
b) Viết phương trình đường tròn đường kính AB
Gọi I là trung điểm của AB
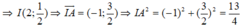
Đường tròn đường kính AB là đường tròn tâm I bán kính IA:

\(\overrightarrow{BA}=\left(2;4\right)\Rightarrow AB=\sqrt{2^2+4^2}=2\sqrt{5}\)
Gọi M là trung điểm AB \(\Rightarrow\left\{{}\begin{matrix}M\left(-1;0\right)\\AM=\dfrac{AB}{2}=\sqrt{5}\end{matrix}\right.\)
Đường tròn đường kính AB có tâm M và bán kính \(R=AM\) nên có pt:
\(\left(x+1\right)^2+y^2=5\)

a, Bán kính: \(R=2\sqrt{5}\)
Phương trình đường tròn: \(\left(x+1\right)^2+\left(y-2\right)^2=20\)
Giao điểm của d và (C) có tọa độ là nghiệm hệ:
\(\left\{{}\begin{matrix}\left(x+1\right)^2+\left(y-2\right)^2=20\\x+3y+5=0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}\left(3y+4\right)^2+\left(y-2\right)^2=20\\x=-3y-5\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}10y^2+20y=0\\x=-3y-5\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}\left\{{}\begin{matrix}y=0\\x=-5\end{matrix}\right.\\\left\{{}\begin{matrix}y=-2\\x=1\end{matrix}\right.\end{matrix}\right.\)
\(\Rightarrow\left\{{}\begin{matrix}M=\left(0;-5\right)\\N=\left(-2;1\right)\end{matrix}\right.\) là các giao điểm
b, Gọi H là trung điểm AB.
Đường thẳng \(\Delta\) vuông góc với d nên có phương trình dạng: \(3x-y+m=0\left(m\in R\right)\)
Ta có: \(S_{IAB}=\dfrac{1}{2}.R^2.sinAIB=10.sinAIB=5\sqrt{3}\)
\(\Rightarrow sinAIB=\dfrac{\sqrt{3}}{2}\)
Mà tam giác ABC tù nên \(\widehat{AIB}=120^o\)
\(\Rightarrow\widehat{HBI}=30^o\)
Khi đó:
\(IH=d\left(I;\Delta\right)\)
\(\Leftrightarrow R.sinHBI=\dfrac{\left|-3-2+m\right|}{\sqrt{10}}\)
\(\Leftrightarrow2\sqrt{5}.sin30^o=\dfrac{\left|m-5\right|}{\sqrt{10}}\)
\(\Leftrightarrow m=5\pm5\sqrt{2}\)
\(\Rightarrow\left[{}\begin{matrix}\Delta:3x-y+5+5\sqrt{2}=0\\\Delta:3x-y+5-5\sqrt{2}=0\end{matrix}\right.\)

a, Bán kính: \(R=2\sqrt{545}\)
Phương trình đường tròn: \(\left(x+1\right)^2+\left(y-2\right)^2=2180\)
Giao điểm của \(\left(C\right);\left(d\right)\) có tọa độ là nghiệm hệ:
\(\left\{{}\begin{matrix}x+3y+5=0\\\left(x+1\right)^2+\left(y-2\right)^2=2180\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x=-3y-5\\\left(-3y-4\right)^2+\left(y-2\right)^2=2180\end{matrix}\right.\)
\(\Leftrightarrow...\)

Đường tròn (C) tâm O(0;0) bán kính R=1
Phương trình đường thẳng IO có dạng: \(y=x\)
Do A;B là giao điểm của 2 đường tròn \(\Rightarrow AB\perp IO\)
Gọi H là trung điểm AB \(\Rightarrow H\in OI\) ; \(AH=\dfrac{AB}{2}=\dfrac{\sqrt{2}}{2}\)
\(\Rightarrow OH=\sqrt{OA^2-AH^2}=\sqrt{1-\dfrac{1}{2}}=\dfrac{\sqrt{2}}{2}\)
Do H thuộc OI nên tọa độ có dạng: \(H\left(x;x\right)\Rightarrow OH=\sqrt{x^2+x^2}=\sqrt{2x^2}\)
\(\Rightarrow\sqrt{2x^2}=\dfrac{\sqrt{2}}{2}\Rightarrow x=\pm\dfrac{1}{2}\) \(\Rightarrow\left[{}\begin{matrix}H\left(\dfrac{1}{2};\dfrac{1}{2}\right)\\H\left(-\dfrac{1}{2};-\dfrac{1}{2}\right)\end{matrix}\right.\)
Đường thẳng AB qua H và vuông góc OI nên nhận \(\left(1;1\right)\) là 1 vtpt có dạng:
\(\left[{}\begin{matrix}1\left(x-\dfrac{1}{2}\right)+1\left(y-\dfrac{1}{2}\right)=0\\1\left(x+\dfrac{1}{2}\right)+1\left(y+\dfrac{1}{2}\right)=0\end{matrix}\right.\) \(\Leftrightarrow\left[{}\begin{matrix}x+y-1=0\\x+y+1=0\end{matrix}\right.\)

a) Để tìm tọa độ tâm và bán kính của đường tròn ©, ta cần viết lại phương trình của nó dưới dạng chuẩn:
\begin{align*}
x^2 + y^2 - 2x + 6y - 2 &= 0 \
\Leftrightarrow (x-1)^2 + (y+3)^2 &= 14
\end{align*}
Vậy, tọa độ tâm của đường tròn © là $(1,-3)$ và bán kính của đường tròn © là $\sqrt{14}$.
b) Đường tròn có tâm $I(4,3)$ và đi qua $A(-4,1)$ có phương trình là:
$$(x-4)^2 + (y-3)^2 = (-4-4)^2 + (1-3)^2 = 20$$
c) Để tìm phương trình đường tròn (C') có tâm là $I(4,3)$ và cắt đường thẳng $d: 3x+4y-4=0$ tại hai điểm $M$ và $N$ sao cho $MN=6$, ta có thể làm như sau:
Tìm giao điểm $H$ của đường thẳng $d$ và đường vuông góc với $d$ đi qua $I$.Tìm hai điểm $M$ và $N$ trên đường thẳng $d$ sao cho $HM=HN=3$.Xây dựng đường tròn (C') có tâm là $I$ và bán kính bằng $IN=IM=\sqrt{3^2+4^2}=5$.
Để tìm giao điểm $H$, ta cần tìm phương trình của đường thẳng vuông góc với $d$ đi qua $I$. Đường thẳng đó có phương trình là:
$$4x - 3y - 7 = 0$$
Giao điểm $H$ của đường thẳng này và $d$ có tọa độ là $(\frac{52}{25}, \frac{9}{25})$.
Để tìm hai điểm $M$ và $N$, ta có thể sử dụng công thức khoảng cách giữa điểm và đường thẳng. Khoảng cách từ điểm $H$ đến đường thẳng $d$ là:
$$d(H,d) = \frac{|3\cdot \frac{52}{25} + 4\cdot \frac{9}{25} - 4|}{\sqrt{3^2+4^2}} = \frac{1}{5}$$
Vậy, hai điểm $M$ và $N$ cách $H$ một khoảng bằng $\frac{3}{5}$ và $\frac{4}{5}$ đơn vị theo hướng vuông góc với $d$. Ta có thể tính được tọa độ của $M$ và $N$ như sau:
$$M = \left(\frac{52}{25} - \frac{4}{5}\cdot 4, \frac{9}{25} + \frac{3}{5}\cdot 3\right) = \left(\frac{12}{25}, \frac{54}{25}\right)$$
và
$$N = \left(\frac{52}{25} + \frac{4}{5}\cdot 4, \frac{9}{25} + \frac{4}{5}\cdot 3\right) = \left(\frac{92}{25}, \frac{27}{5}\right)$$
Cuối cùng, phương trình đường tròn (C') có tâm là $I(4,3)$ và cắt đường thẳng $d$ tại hai điểm $M$ và $N$ sao cho $MN=6$ là:
$$(x-4)^2 + (y-3)^2 = 5^2$$
Tọa độ tâm I là:
x=(4-2)/2=1 và y=(-1+5)/2=2
I(1;2); A(4;-1)
\(IA=\sqrt{\left(4-1\right)^2+\left(-1-2\right)^2}=3\sqrt{2}\)
=>Phương trình đường tròn là:
(x-1)^2+(y-2)^2=18