Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a/ CD qua E và vuông góc BC nên pt có dạng:
\(1\left(x-6\right)-1\left(y-0\right)=0\Leftrightarrow x-y-6=0\)
Ta có: \(AB=d\left(A;BC\right)=\frac{\left|3+5-2\right|}{\sqrt{1^2+1^2}}=3\sqrt{2}\)
\(AD=d\left(A;CD\right)=\frac{\left|3-5-6\right|}{\sqrt{1^2+\left(-1\right)^2}}=4\sqrt{2}\)
\(\Rightarrow S_{ABCD}=AB.AD=24\)
b/ Do M thuộc d nên tọa độ có dạng: \(M\left(1+t;2-3t\right)\)
Áp dụng công thức khoảng cách:
\(d\left(M;\Delta\right)=4\Leftrightarrow\frac{\left|3\left(1+t\right)+4\left(2-3t\right)+5\right|}{\sqrt{3^2+4^2}}=4\)
\(\Leftrightarrow\left|16-9t\right|=20\Rightarrow\left[{}\begin{matrix}16-9t=20\\16-9t=-20\end{matrix}\right.\)
\(\Rightarrow\left[{}\begin{matrix}t=-\frac{4}{9}\\t=4\end{matrix}\right.\) \(\Leftrightarrow\left[{}\begin{matrix}M\left(\frac{5}{9};\frac{10}{3}\right)\\M\left(5;-10\right)\end{matrix}\right.\)

a: vecto AB=(6;-4)
PTTS là:
x=-6+6t và y=3-4t
b: Vì (d) vuông góc AB nên (d) có VTPT là (3;-2)
Phương trình(d) là:
3(x-3)+(-2)(y-2)=0
=>3x-9-2y+4=0
=>3x-2y-5=0

Câu 1:
Do \(\Delta\) song song d nên nhận \(\left(2;-1\right)\) là 1 vtpt
Phương trình \(\Delta\) có dạng: \(2x-y+c=0\) (\(c\ne2015\))
Tọa độ giao điểm của \(\Delta\) và Ox: \(\left\{{}\begin{matrix}y=0\\2x-y+c=0\end{matrix}\right.\) \(\Rightarrow M\left(-\frac{c}{2};0\right)\)
Tọa độ giao điểm \(\Delta\) và Oy: \(\left\{{}\begin{matrix}x=0\\2x-y+c=0\end{matrix}\right.\) \(\Rightarrow N\left(0;c\right)\)
\(\overrightarrow{MN}=\left(\frac{c}{2};c\right)\Rightarrow\frac{c^2}{4}+c^2=45\Leftrightarrow c^2=36\Rightarrow\left[{}\begin{matrix}c=6\\c=-6\end{matrix}\right.\)
Có 2 đường thẳng thỏa mãn: \(\left[{}\begin{matrix}2x-y+6=0\\2x-y-6=0\end{matrix}\right.\)
Bài 2:
Bạn tham khảo ở đây:
Câu hỏi của tôn hiểu phương - Toán lớp 10 | Học trực tuyến

Phương trình hoành độ giao điểm:
\(x^2+2x-m+1=x+1\)
\(\Leftrightarrow x^2+x-m=0\left(1\right)\)
\(\left(d\right),\left(P\right)\) cắt nhau tại hai điểm phân biệt khi phương trình \(\left(1\right)\) có hai nghiệm phân biệt
\(\Leftrightarrow\Delta=4m+1>0\Leftrightarrow m>-\dfrac{1}{4}\)
Phương trình \(\left(1\right)\) có hai nghiệm phân biệt \(x=\dfrac{-1\pm\sqrt{4m+1}}{2}\)
\(x=\dfrac{-1+\sqrt{4m+1}}{2}\Rightarrow y=\dfrac{1+\sqrt{4m+1}}{2}\Rightarrow A\left(\dfrac{-1+\sqrt{4m+1}}{2};\dfrac{1+\sqrt{4m+1}}{2}\right)\)
\(x=\dfrac{-1-\sqrt{4m+1}}{2}\Rightarrow y=\dfrac{1-\sqrt{4m+1}}{2}\Rightarrow B\left(\dfrac{-1-\sqrt{4m+1}}{2};\dfrac{1-\sqrt{4m+1}}{2}\right)\)
\(AB=8\Leftrightarrow\sqrt{8m+2}=8\Leftrightarrow m=\dfrac{31}{4}\left(tm\right)\)
2.
a, \(AB=2\sqrt{5},BC=5\sqrt{10},CA=\sqrt{170}\)
\(AM^2=\dfrac{AB^2+AC^2}{2}-\dfrac{BC^2}{4}=\dfrac{65}{2}\Rightarrow AM=\dfrac{\sqrt{130}}{2}\)
b, \(\left\{{}\begin{matrix}x_D-4-2\left(x_D-2\right)+4\left(x_D+3\right)=0\\y_D-3-2\left(y_D-7\right)+4\left(y_D+8\right)=0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x_D=-4\\y_D=-\dfrac{14}{3}\end{matrix}\right.\)
\(\Rightarrow D\left(-4;-\dfrac{14}{3}\right)\)
c, \(\left\{{}\begin{matrix}\overrightarrow{AA'}=\left(x_{A'}-4;y_{A'}-3\right)\\\overrightarrow{BC}=\left(-5;-15\right)\\\overrightarrow{BA'}=\left(x_{A'}-2;y_{A'}-7\right)\end{matrix}\right.\)
\(AA'\perp BC\Leftrightarrow\left\{{}\begin{matrix}\overrightarrow{AA'}.\overrightarrow{BC}=0\left(1\right)\\\overrightarrow{BA'}=k\overrightarrow{BC}\left(2\right)\end{matrix}\right.\)
\(\left(1\right)\Leftrightarrow-5\left(x_{A'}-4\right)-15\left(y_{A'}-3\right)=0\Leftrightarrow x_{A'}+3y_{A'}=13\)
\(\left(2\right)\Leftrightarrow\left\{{}\begin{matrix}x_{A'}-2=-5k\\y_{A'}-7=-15k\end{matrix}\right.\Leftrightarrow3x_{A'}-y_{A'}=-1\)
\(\left\{{}\begin{matrix}x_{A'}+3y_{A'}=13\\3x_{A'}-y_{A'}=-1\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x_{A'}=1\\y_{A'}=4\end{matrix}\right.\Rightarrow A'\left(1;4\right)\)

A(m-1;-1); B(2;2-2m); C(m+3;3)
\(\overrightarrow{AB}=\left(2-m+1;2-2m+1\right)\)
=>\(\overrightarrow{AB}=\left(3-m;3-2m\right)\)
\(\overrightarrow{AC}=\left(m+3-m+1;3+1\right)\)
=>\(\overrightarrow{AC}=\left(4;4\right)\)
Để A,B,C thẳng hàng thì \(\dfrac{3-m}{4}=\dfrac{3-2m}{4}\)
=>3-m=3-2m
=>m=0
\(\left\{{}\begin{matrix}\overrightarrow{AB}=\left(3-m;3-2m\right)\\\overrightarrow{AC}=\left(4;4\right)\end{matrix}\right.\)
3 điểm A;B;C thẳng hàng khi và chỉ khi \(\overrightarrow{AB}=k\overrightarrow{AC}\) với \(k\ne0\)
Hay \(\dfrac{3-m}{4}=\dfrac{3-2m}{4}\Rightarrow m=0\)
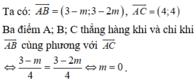

Điểm A cho là thừa.
M là giao của 2 đường thẳng BC và đường thẳng y = 3.
Đường thẳng BC là (đi qua B và C):
\(\frac{y-y_B}{y_C-y_B}=\frac{x-x_B}{x_C-x_B}\) hay là \(\frac{y-2}{5-2}=\frac{x-1}{2-1}\) hay là y = 3x - 1
Giao của hai đường thẳng y = 3x -1 và y = 3 là điểm có hoành độ thỏa mãn:
3x - 1 = 3 => x = 4/3
Vậy điểm M có tọa độ: (4/3 ; 3)
có j lên mạng á bạn