Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Trên cùng một nửa mặt phẳng bờ chứa tia OA có C O A ^ < B O A ^ nên tia OC nằm giữa hai tia OA, OB

hình thì tự vẽ
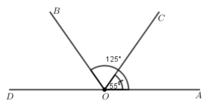
trên nửa mặt phẳng oa có 2 tia oc ob , boa=145,coa=55 mà coa<boa (55<145) suy ra tia oc nằm giữa tia 0b và oa nêm ta có hệ thức
boc+ coa=boa
suy ra boc+ 55=145
boc=145-55
boc =90

Trên cùng 1 nửa mặt phẳng bờ chứa tia OA có tia OC nằm giữa tia OB và OC
=> COA + COB = BOA (Thay số)
=> 55* + COB = 145*
=> COB = 145* - 55*
Vậy: COB = 90*

a ) Trên nửa mặt phẳng bờ chứa tia At , có hai tia Ay và Ax , tAx < tAy
\(\Rightarrow\) 75o < 150o
\(\Rightarrow\) Tia Ax nằm giữa hai tia còn lại .
b ) Trên nửa mặt phẳng bờ chứa tia OA có góc AOB = 1200 ; góc AOC = 1050
\(\Rightarrow\) góc AOB > góc AOC ( 120 > 105 )
\(\Rightarrow\) Tia OC nằm giữa 2 tia OA và OB .

55 độ O A B C 145 độ
Ta có \(\widehat{BOA}=\widehat{AOC}+\widehat{BOC}\)
Hay 145o = 55o + \(\widehat{BOC}\)
=> \(\widehat{BOC}\)= 145o - 55o = 90o
Vậy góc BOC = 90o

a) Trên cùng 1 nửa mp bờ chứa tia Oa có:
\(\widehat{aOb}< \widehat{aOc}\left(50^o< 100^o\right)\)
=> Ob nằm giữa Oa và Oc
Vậy Ob nằm giữa hai tia Oa và Oc
b) Vì Ob nằm giữa Oa và Oc nên:
\(\widehat{aOb}+\widehat{bOc}=\widehat{aOc}\)
=> 50o + \(\widehat{bOc}\) = 100o
hay \(\widehat{bOc}=100^o-50^o\)
\(\widehat{bOc}=50^o\)
Vậy \(\widehat{bOc}=50^o\)
c) Ta có: Ob nằm giữa Oa và Oc (1)
\(\widehat{aOb}=\widehat{bOc}\left(=50^o\right)\) (2)
Từ (1) và (2) suy ra Ob là tia phân giác của góc aOc
Vậy Ob là tia phân giác của \(\widehat{aOc}\)
a) Trên cùng một nữa mặt phẳng có bờ chưa tia Oa.
Có góc : aOb = 50o và aOc = 100o
=> Góc aOB < aOc
=> Tia Ob nằm giữa hai tia Oa và Oc.
b) Tia Ob nằm giữa hai tia Oa và Oc
=> aOb + bOc = aOc
=> 50 + bOc = 100
=> bOc = 100 - 50
=> bOc = 50o
Ta có tia Ob nằm giữa hai tia Oa và Oc
Và aOb = bOc = 50o
Vậy Ob là tia phân giác của góc aOc