Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đặt \(A=\frac{1}{2}+\frac{1}{4}+\frac{1}{8}+\frac{1}{16}+\frac{1}{32}+\frac{1}{64}+\frac{1}{128}\)
\(\Rightarrow2A=1+\frac{1}{2}+\frac{1}{4}+\frac{1}{16}+\frac{1}{32}+\frac{1}{64}\)
\(\Rightarrow2A-A=1-\frac{1}{128}=\frac{127}{128}\)

a, Số số hạng của dãy số là 9(số);
=> Tổng của dãy số là (9+1)*9/2=45
b,Số số hạng của dãy số là 50 số
=> Tổng của dãy số là (50+1)*50/2=1275
c, Số số hạng của dãy số là (99-1)/2+1=50 số
=> Tổng của dãy số là (99+1)*50/2= 2500

B)A*2=(1/2+1/4+....+1/256)*2
=1+1/2+1/4+....+1/128)
A*2-A=(1+1/2+1/4+...+1/128)-(1/2+1/4+...+1/256)
=1-1/256
=255/256
a) Đặt A = \(\frac{5}{2}+\frac{5}{6}+\frac{5}{18}+\frac{5}{54}+\frac{5}{162}\)
\(\Rightarrow\frac{1}{3}\times A=\frac{5}{6}+\frac{5}{18}+\frac{5}{54}+\frac{5}{162}+\frac{5}{486}\)
Lấy \(A-\frac{1}{3}\times A\)theo vế ta có :
\(A-\frac{1}{3}\times A=\left(\frac{5}{2}+\frac{5}{6}+\frac{5}{18}+\frac{5}{54}+\frac{5}{162}\right)-\left(\frac{5}{6}+\frac{5}{18}+\frac{5}{54}+\frac{5}{162}+\frac{5}{486}\right)\)
\(\Rightarrow\frac{2}{3}\times A=\frac{5}{2}-\frac{5}{486}\)
\(\Rightarrow\frac{2}{3}\times A=\frac{605}{243}\)
\(\Rightarrow A=\frac{605}{243}:\frac{2}{3}\)
\(\Rightarrow A=\frac{605}{162}\)
Vậy \(\frac{5}{2}+\frac{5}{6}+\frac{5}{18}+\frac{5}{54}+\frac{5}{162}=\frac{605}{162}\)
b) Đặt B = \(\frac{1}{2}+\frac{1}{4}+\frac{1}{8}+...+\frac{1}{128}+\frac{1}{256}\)
=> \(\frac{1}{2}\times B=\frac{1}{4}+\frac{1}{8}+\frac{1}{16}+...+\frac{1}{256}+\frac{1}{512}\)
Lấy B trừ \(\frac{1}{2}\times B\)theo vế ta có :
\(B-\frac{1}{2}\times B=\left(\frac{1}{2}+\frac{1}{4}+\frac{1}{6}+...++\frac{1}{128}+\frac{1}{256}\right)-\left(\frac{1}{4}+\frac{1}{6}+\frac{1}{8}+...+\frac{1}{512}\right)\)
\(\Rightarrow\frac{1}{2}\times B=\frac{1}{2}-\frac{1}{512}\)
\(\Rightarrow\frac{1}{2}\times B=\frac{255}{512}\)
\(\Rightarrow B=\frac{255}{512}:\frac{1}{2}\)
\(\Rightarrow B=\frac{255}{256}\)
Vậy \(\frac{1}{2}+\frac{1}{4}+\frac{1}{8}+\frac{1}{16}+...+\frac{1}{256}=\frac{255}{256}\)

Bài 1:
Ta thấy: 1 + 2 = 3 3 + 5 = 8
2 + 3 = 5 5 + 8 = 13
Dãy số trên được lập theo quy luật sau: Kể từ số hạng thứ 3 trở đi mỗi số hạng bằng tổng của hai số hạng đứng liền trước nó.
Ba số hạng tiếp theo là: 21 + 34 = 55; 34 + 55 = 89; 55 + 89 = 144
Vậy dãy số được viết đầy đủ là: 1, 2, 3, 5, 8, 13, 34, 55, 89, 144
Bài 2:
Ta nhận thấy: 8 = 1 + 3 + 4 27 = 4+ 8 + 15
15 = 3 + 4 + 8
Từ đó ta rút ra được quy luật của dãy số là: Mỗi số hạng (kể từ số hạng thứ 4) bằng tổng của ba số hạng đứng liền trước nó.
Viết tiếp ba số hạng, ta được dãy số sau: 1, 3, 4, 8, 15, 27, 50, 92, 169.
Bài 3:
Giải:
a). Ta nhận xét :
Số hạng thứ 10 là : 1024 = 512 x 2
Số hạng thứ 9 là : 512 = 256 x 2
Số hạng thứ 8 là : 256 = 128 x 2
Số hạng thứ 7 là : 128 = 64 x 2
……………………………..
Từ đó ta suy luận ra quy luật của dãy số này là: mỗi số hạng của dãy số gấp đôi số hạng đứng liền trước đó.
Vậy số hạng đầu tiên của dãy là: 1 x 2 = 2.
b). Ta nhận xét :
Số hạng thứ 10 là : 110 = 11 x 10
Số hạng thứ 9 là : 99 = 11 x 9
Số hạng thứ 8 là : 88 = 11 x 8
Số hạng thứ 7 là : 77 = 11 x 7
…………………………..
Từ đó ta suy luận ra quy luật của dãy số là: Mỗi số hạng bằng số thứ tự của số hạng ấy nhân với 11.
Vậy số hạng đầu tiên của dãy là : 1 x 11 = 11.
bài 1:
các số đó là : 55, 89, 144
bài 2 :
đề bài sai, mk nghĩ thế ( mong online math đừng trừ điểm nhé )
bài 3 :
a, nhận xét :
ta thấy : số hạng thứ 10 = 1024 = 2 . 2 . 2 . 2 . 2 . 2 . 2 . 2 . 2 . 2 ( 10 số 2 )
số hạng thứ 9 = 512 = 2 . 2 . 2 . 2 . 2 . 2 . 2 . 2 . 2 ( 9 số 2 )
tương tự, ta có :
số hạng thứ 8 = 8 số 2 nhân với nhau
số hạng thứ 7 = 7 số 2 nhân với nhau
=> số hạng thứ 1 = 2
b, gọi số hạng đầu tiên là x, ta có :
( 110 - x ) : 11 + 1 = 10 ( theo công thức tìm số số hạng )
110 - x = ( 10 - 1 ) . 11
110 - x = 99
x = 110 - 99
x = 11
vậy số hạng đầu tiên của dãy là 11
kick mk nha
thank you very much

Cộng thêm 1/2 vào biểu thức đã cho, có:
S + 1/2= 1/2+1/4+ 1/8+ 1/16+1/32+1/64+1/128
Nhận xét:
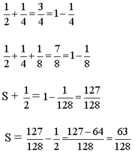

gọi tổng đó là A ta có :
A = 1/2 + 1/4 + 1/8 +1/16 + 1/32 +1/64 + 1/128
2A= ( 1/2 * 2) + ( 1/4 * 2 ) + ( 1/8 * 2) + ( 1/16 * 2) + ( 1/32 * 2 ) + ( 1/64 * 2 ) + ( 1/128 * 2)
2A= 1+ 1/2 + 1/4 + 1/8 + 1/16 + 1/32 + 1/64
TA LẤY 2A - 1A = 1A
A = ( 1 + 1/2 +1/4 + 1/8 + 1/16 + 1/32 + 1/64 ) - ( 1/2 + 1/4 + 1/8 + 1/16 + 1/32 + 1/64 + 1/128 )
TA THẤY 1/2 - 1/2 = 0 ; 1/4 - 1/4 = 0 ; 1/8 - 1/8 = 0 ;1/16 - 1/16 = 0 ; 1/32 - 1/32 = 0 ; 1/64- 1/64 = 0
NÊN A = 1 - 1/128 = 127/128
gọi tổng đó là A ta có :
A = 1/2 + 1/4 + 1/8 +1/16 + 1/32 +1/64 + 1/128
2A= ( 1/2 * 2) + ( 1/4 * 2 ) + ( 1/8 * 2) + ( 1/16 * 2) + ( 1/32 * 2 ) + ( 1/64 * 2 ) + ( 1/128 * 2)
2A= 1+ 1/2 + 1/4 + 1/8 + 1/16 + 1/32 + 1/64
TA LẤY 2A - 1A = 1A
A = ( 1 + 1/2 +1/4 + 1/8 + 1/16 + 1/32 + 1/64 ) - ( 1/2 + 1/4 + 1/8 + 1/16 + 1/32 + 1/64 + 1/128 )
TA THẤY 1/2 - 1/2 = 0 ; 1/4 - 1/4 = 0 ; 1/8 - 1/8 = 0 ;1/16 - 1/16 = 0 ; 1/32 - 1/32 = 0 ; 1/64- 1/64 = 0
NÊN A = 1 - 1/128 = 127/128
a) Số các số hạng là:
( 99-49):2+1\(=\)26 ( số )
Tổng của dãy số trên là:
( 99 + 49 ) x 26 : 2 \(=\)1924
Đáp số: 1924
b) \(\frac{1}{2}+\frac{1}{4}+\frac{1}{8}+\frac{1}{16}+\frac{1}{32}+\frac{1}{64}+\frac{1}{128}\)
\(=\frac{1}{1}-\frac{1}{2}+\frac{1}{2}-\frac{1}{4}+\frac{1}{4}-\frac{1}{8}+\frac{1}{8}-\frac{1}{16}+\frac{1}{16}-\frac{1}{32}+\frac{1}{32}-\frac{1}{64}+\frac{1}{64}-\frac{1}{128}\)
\(=\frac{1}{1}-\frac{1}{128}\)
\(=\frac{127}{128}\)
a) Số các số hạng là (99 - 49) : 2 + 1 = 26 số
Tổng của dãy trên là:
(99 + 49) x 26 : 2 = 1924
Đáp số : 1924
b) 1/2 + 1/4 + 1/8 + 1/16 + 1/32 + 1/64 + 1/128
= 1/1 - 1/2 + 1/2 - 1/4 + 1/4 - 1/8 + 1/8 - 1/16 + 1/16 - 1/32 + 1/32 - 1/64 + 1/64 - 1/128
= 1/1 - 1/128
= 127/128