
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Sửa đề: x=21
=>x-1=20
\(A=x^{10}+x^9\left(x-1\right)+x^8\left(x-1\right)+...+x^3\left(x-1\right)+x^2\left(x-1\right)+x\left(x-1\right)\)
\(=x^{10}+x^{10}-x^9+x^9-x^8+...+x^3-x^2+x^2-x\)
\(=2x^{10}-x=2\cdot21^{10}-21\)

Lời giải:
\(A=x^{10}+20x^9+20x^8+...+20x^3+20x^2+20x\)
\(=x^{10}+21x^9+21x^8+....+21x^3+21x^2+21x-(x^9+x^8+...+x^3+x^2+x)\)
\(=x^{10}-x.x^9-x.x^8-...-x.x^3-x.x^3-x.x-(x^9+x^8+...+x^3+x^2+x)\)
\(=-(x^9+x^8+....+x^2)-(x^9+x^8+x^3+x^2+x)\)
\(=-2(x^2+x^3+...+x^9)-x\)
\(Ax=-2(x^3+x^4+...+x^{10})-x^2\)
\(Ax-A=-2(x^3+x^4+...+x^{10})-x^2+2(x^2+...+x^9)+x\)
\(A(x-1)=x^2+x-2x^{10}\)
\(A=\frac{x^2+x-2x^{10}}{x-1}=\frac{21^2-21-2.21^{10}}{-22}=\frac{21^{10}-210}{11}\)

Ta có: \(x=-24\Leftrightarrow-x=24\Leftrightarrow1-x=25\)
Thay vào E ta được:
\(E=x^{20}+\left(1-x\right)x^{19}+\left(1-x\right)x^{18}+...+\left(1-x\right)x^2+\left(1-x\right)x+\left(1-x\right)\)
\(E=x^{20}+x^{19}-x^{20}+x^{18}-x^{19}+...+x^2-x^3+x-x^2+1-x\)
\(E=1\)

\(x=7\Rightarrow\left\{{}\begin{matrix}4=x-3\\20=3x-1\end{matrix}\right.\)\(\Rightarrow P\left(7\right)=x^{100}-4x^{99}-20x^{98}-4x^{97}-...-20x^2-4x\\ =x^{100}-\left(x-3\right)x^{99}-\left(3x-1\right)x^{98}-\left(x-3\right)x^{97}-...-\left(3x-1\right)x^2-\left(x-3\right)x\\ =x^{100}-x^{100}+3x^{99}-3x^{99}+x^{98}-x^{98}+3x^{97}-...-3x^3+x^2-x^2+3x\\ =3x\\ =21\)

Thay x = 20 vào biểu thức B ta có
\(B=x^6-x.x^5-x.x^4-x.x^3-x.x^2-x.x+3\)
\(=x^6-x^6-x^5-x^4-x^3-x^2+3\)
\(=-x^5-x^4-x^3-x^2+3\)
\(=-x^2\left(x^3+x^2+x+1\right)+3\)
\(=-20^2\left(20^3+20^2+20+1\right)+3\)
\(=-400\left(8000+400+20+1\right)+3\)
\(=-400.8421+3\)
\(=-3368397\)
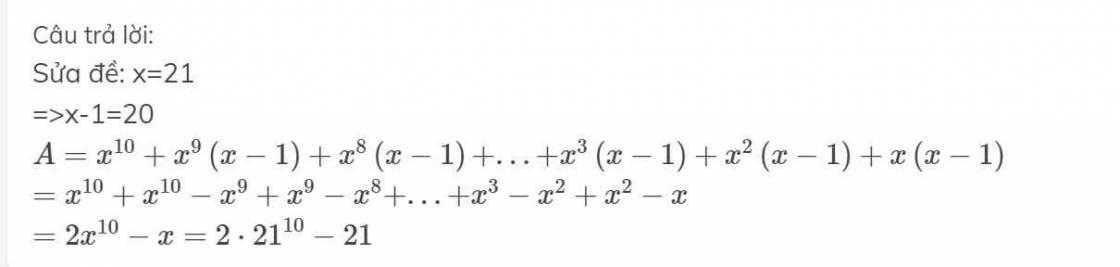
bài này tớ ko hiểu qui luật