K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
SG
5
TP
18 tháng 4 2017
a) Ta có: 1.120 = 2.60 = 4.30 = 5.24 =8.15 = 120
Nên x và y là hai đại lượng tỉ lệ nghịch với nhau.
b) Vì 5.12,5 ≠ 6.10 nên x và y không tỉ lệ nghịch với nhau.
VK
18 tháng 4 2017
Gọi k là hệ số tỉ lệ giữa x và y
a) Ta có:
\(1.120=2.60=4.30=5.24=8.15=k=120\)
\(\Rightarrow\) Hai đại lượng x và y tỉ lệ nghịch với nhau.
b) Ta có:
\(2.30=3.20=4.15=6.10=k=120\)
Mà: \(5.12,5=62.5\ne120\)
\(\Rightarrow\) Hai đại lượng x và y không tỉ lệ nghịch với nhau
27 tháng 5 2017
Ta có : AB=AC
=> \(\Delta ABC\) là tam giác vuông cân tại A ( vì tam giác có 2 cạnh bằng nhau )
=> \(\widehat{ABC}=A\widehat{CB}\) ( hai cạnh đáy của tam giác cân )
=> \(\widehat{ABC}=A\widehat{CB}=45^0\)
=> \(\widehat{CBD}=\widehat{A}+\widehat{BCA}=135^0\) ( góc ngoài của tam giác )
Ta lại có:
BD=BC
=> \(\Delta BCD\) cân tại B ( vì tam giác có 2 cạnh bằng nhau )
=> \(\widehat{BDC}=\widehat{BCD}\) ( hai cạnh đáy của tam giác cân )
=> \(\widehat{BDC}=\widehat{BCD}=\dfrac{\left(180^0-135^0\right)}{2}=\dfrac{45^0}{2}=22,5^0\)
Mà \(\widehat{ACD}=\widehat{BCA}+\widehat{BCD}\)
=> \(\widehat{ACD}=45^0+22,5^0=67,5^0\)
Vậy trong \(\Delta ACD\) có :
\(\left\{{}\begin{matrix}\widehat{A}=90^0\\\widehat{ADC}=22,5^0\\\widehat{ACD}=67,5^0\end{matrix}\right.\)
19 tháng 4 2017
Ghép a-d' ; b –a', c-b', d-c'
Trong một tam giác
a - d' đường phân giác xuất phát từ đỉnh A - là đoạn thẳng có hai mút là đỉnh A và giao điểm của cạnh BC với tia phân giác của góc A.
b - a' đường trung trực ứng với cạnh BC - là đường vuông góc với cạnh BC tại trung điểm của nó.
c - b' đường cao xuất phát từ đỉnh A - là đoạn vuông góc kẻ từ A đến đường thẳng BC.
d - c' đường trung tuyến xuất phát từ đỉnh A - là đoạn thẳng nối A với trung điểm của cạnh BC.
19 tháng 4 2017
Trả lời
Ghép a-d' ; b –a', c-b', d-c'
Trong một tam giác
a - d' đường phân giác xuất phát từ đỉnh A - là đoạn thẳng có hai mút là đỉnh A và giao điểm của cạnh BC với tia phân giác của góc A.
b - a' đường trung trực ứng với cạnh BC - là đường vuông góc với cạnh BC tại trung điểm của nó.
c - b' đường cao xuất phát từ đỉnh A - là đoạn vuông góc kẻ từ A đến đường thẳng BC.
d - c' đường trung tuyến xuất phát từ đỉnh A - là đoạn thẳng nối A với trung điểm của cạnh BC.
SG
1
LV
20 tháng 4 2017
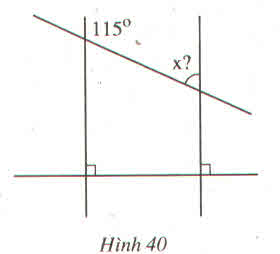
Đáp án và hướng dẫn giải bài 58:
Ta có: a⊥c; b⊥c ⇒ a//b ( hai đường thẳng cùng vuông góc đường thẳng thứ ba)
⇒ ∠A + ∠B = 1800 (2 góc trong cùng phía)
⇒ 1150 + ∠B = 1800
⇒∠B = 650
20 tháng 4 2017
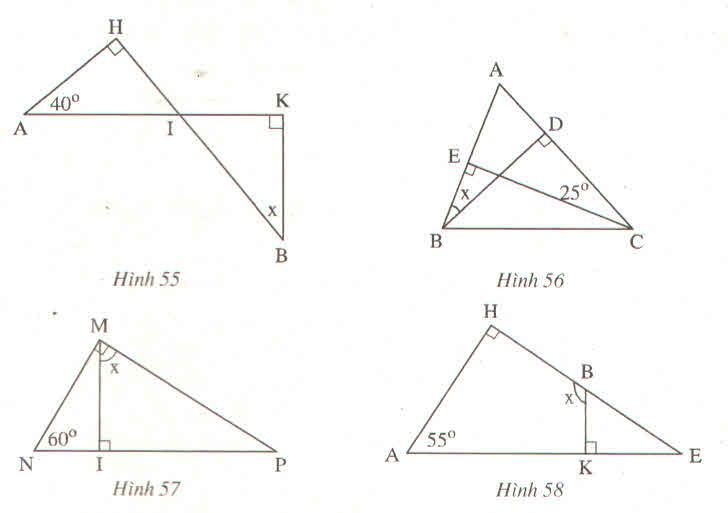
Hình 55:
Ta có ∠A + ∠AIH = 900 (Vì tam giác AHI cân tại H) ⇒∠AIH = 900 – 400 = 500
mà ∠AIH = ∠BIK( 2 góc đối đỉnh) ⇒∠BIK = 500
Ta lại có: ∠IBK +∠BIK = 900 (Vì tam giác IKB cân tại K)
⇒ ∠IBK = 900 – 500 = 400
⇒ x = 400
Hình 56:
Các em có thể giải theo cách của bài 55 tuy nhiên là hơi dài và chúng ta có cách khác làm nhanh hơn. (Áp dụng hình 56 và các hình sau nhé)
Ta có :
Xét tam giác ABD cân tại D ta có ∠ABD + ∠BAD = 900
Xét tam giác ACE cân tại E ta có ∠ACE + ∠EAC = 900
Mà ta có ∠BAD cũng chính là góc ∠EAC
Suy ra ∠ABD = ∠ACE = 250
Vậy ∠ABD = 250 => x = 250
Hình 57:
Xét tam giác MNP vuông tại M ⇒ ∠MNP+ ∠MPN = 900
⇔ 600 + ∠MPN = 900
⇒ ∠MPN = 900 – 600 = 300
Tiếp tục xét tam giác IMP vuông tại I ⇒ ∠IMP + ∠IPM = 900
⇔ ∠IMP + 300 = 900 ( vì∠IPM = ∠MPN )
⇒∠IMP = 900 – 300 = 600
Vậy ∠IMP = 600 => x = 600
Hình 58:
Ta có
Xét tam gác HAE vuông tại H nên ta có ∠HEA = 900 – ∠HAE = 900 – 550 = 350
hay chính là góc ∠BEK = 350
Ta có: ∠HBK = ∠BEK + ∠BKE (Góc ngoài tam giác BKE)
⇒ ∠HBK = 350+ 900 = 1250
Vậy x = 1250
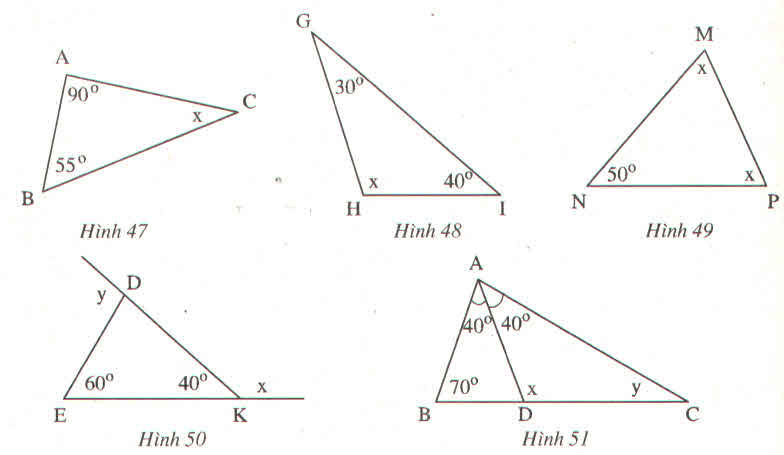
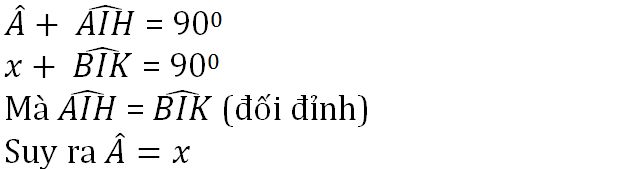
Hình 47:
x+ 900 + 550 = 1800
⇒ x = 1800 – ( 900+ 550)= 350
Hình 48:
x+ 400 + 300 = 1800
⇒ x= 1800 – ( 400+ 390)= 1100
Hình 49:
x+ x + 500= 1800
⇒2x= 1800 – 500 = 1300
⇒ x= 1300 : 2 = 650
Hình 50:
y = 600 + 400= 1000 (Mỗi góc ngoài của một tam giác bằng tổng hai góc không kề với nó)
Ta có: x + 400 = 1800 (kề bù)
⇒x = 1800 – 400 = 1400
Hình 51:
Trong ∆ ABC có
(400+ 400) + 700 + y = 1800
⇒ y + 1500 = 1800
⇒ y = 1800 – 1500= 300
Trong ∆ ACD có:
x + 400 + 300= 1800 ( Góc y = 300 giải được ở trên)
x= 1800 – ( 400+ 300)= 1100