Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a: Ta có:
\(\left(\dfrac{2}{5}+\dfrac{1}{5}\right)+\dfrac{1}{5}=\dfrac{3}{5}+\dfrac{1}{5}=\dfrac{4}{5}\)
\(\dfrac{2}{5}+\left(\dfrac{1}{5}+\dfrac{1}{5}\right)=\dfrac{2}{5}+\dfrac{2}{5}=\dfrac{4}{5}\)
\(\dfrac{4}{5}=\dfrac{4}{5}\). Vậy \(\left(\dfrac{2}{5}+\dfrac{1}{5}\right)+\dfrac{1}{5}=\dfrac{2}{5}+\left(\dfrac{1}{5}+\dfrac{1}{5}\right)\)
Ta có:
\(\left(\dfrac{2}{9}+\dfrac{5}{9}\right)+\dfrac{1}{9}=\dfrac{7}{9}+\dfrac{1}{9}=\dfrac{8}{9}\)
\(\dfrac{2}{9}+\left(\dfrac{5}{9}+\dfrac{1}{9}\right)=\dfrac{2}{9}+\dfrac{6}{9}=\dfrac{8}{9}\)
\(\dfrac{8}{9}=\dfrac{8}{9}\). Vậy \(\left(\dfrac{2}{9}+\dfrac{5}{9}\right)+\dfrac{1}{9}=\dfrac{2}{9}+\left(\dfrac{5}{9}+\dfrac{1}{9}\right)\)
b: \(\left(\dfrac{1}{3}+\dfrac{2}{3}\right)+\dfrac{4}{3}=\dfrac{3}{3}+\dfrac{4}{3}=\dfrac{7}{3}\)
\(\dfrac{1}{3}+\left(\dfrac{2}{3}+\dfrac{4}{3}\right)=\dfrac{1}{3}+\dfrac{6}{3}=\dfrac{7}{3}\)
\(\dfrac{7}{3}=\dfrac{7}{3}\). Vậy \(\left(\dfrac{1}{3}+\dfrac{2}{3}\right)+\dfrac{4}{3}=\dfrac{1}{3}+\left(\dfrac{2}{3}+\dfrac{4}{3}\right)\)
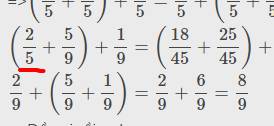
Đề của anh bị sai mới đúng chứ ạ? Anh Đạt ghi là \(\left(\dfrac{2}{9}+\dfrac{5}{9}\right)+\dfrac{1}{9}\) chứ có phải \(\dfrac{2}{5}\) đâu ạ?

\(\left(1-\frac{1}{2}\right)\left(1-\frac{1}{3}\right)\left(1-\frac{1}{4}\right).....\left(1-\frac{1}{100}\right).200x=4036\)
\(\Leftrightarrow\frac{1}{2}.\frac{2}{3}.\frac{3}{4}.....\frac{99}{100}.200x=4036\)
\(\Leftrightarrow\frac{1.2.3...99}{2.3.4....100}.200x=4036\)
\(\Leftrightarrow\frac{1}{100}.200x=4036\)
\(\Leftrightarrow\frac{1}{100}.200x=4036\)
\(\Leftrightarrow2x=4036\)
\(\Leftrightarrow x=4036:2=2018\)
\(\left(1-\frac{1}{2}\right)\times\left(1-\frac{1}{3}\right)\times...\times\left(1-\frac{1}{100}\right)\times200\times x=4036\)
=> \(\frac{1}{2}\times\frac{2}{3}\times...\times\frac{99}{100}\times200\times x=4036\)
=> \(\frac{1\times2\times...\times99}{2\times3\times...\times100}\times200\times x=4036\)
\(\Rightarrow\frac{1}{100}\times200\times x=4036\)
\(\Rightarrow2\times x=4036\)
=> x = 2018

1 \(A=\left(1+\frac{1}{2}\right)\times\left(1+\frac{1}{3}\right)\times\left(1+\frac{1}{4}\right)\times.........\times\left(1+\frac{1}{2016}\right)\times\left(1+\frac{1}{2017}\right)\)
\(A=\frac{3}{2}\times\frac{4}{3}\times\frac{5}{4}\times......\times\frac{2016}{2017}\times\frac{2018}{2017}\)
\(A=\frac{2018}{2}=1009\)
\(B=\frac{2}{3.5}+\frac{2}{5.7}+\frac{2}{7.9}+.......+\frac{2}{43.45}\)
\(B=\frac{1}{3}-\frac{1}{5}+\frac{1}{5}-\frac{1}{7}+\frac{1}{7}-......+\frac{1}{43}-\frac{1}{45}\)
\(B=\frac{1}{3}-\frac{1}{45}\)
\(B=\frac{14}{45}\)
2 \(\frac{2017}{2018}\times\frac{23}{47}+\frac{24}{2018}\times\frac{2017}{47}\)
\(=\frac{2017}{2018}\times\frac{23}{47}+\frac{24}{47}\times\frac{2017}{2018}\)
\(=\frac{2017}{2018}\times\left(\frac{23}{47}+\frac{24}{47}\right)\)
\(=\frac{2017}{2018}\times1\)
=\(\frac{2017}{2018}\)
bạn nào xem giải thế có đúng ko

\(a,\frac{1}{2\times3}+\frac{1}{3\times4}+\frac{1}{4\times5}+\frac{1}{5\times6}=\frac{1}{2}-\frac{1}{3}+\frac{1}{3}-\frac{1}{4}+\frac{1}{4}-\frac{1}{5}+\frac{1}{5}-\frac{1}{6}\)
\(=\frac{1}{2}-\frac{1}{6}=\frac{1}{3}\)
\(b,\left(1-\frac{1}{2}\right)\times\left(1-\frac{1}{3}\right)\times\left(1-\frac{1}{4}\right)=\frac{1}{2}\times\frac{2}{3}\times\frac{3}{4}\)
\(=\frac{1\times2\times3}{2\times3\times4}=\frac{1}{4}\)

\(\left(2.8x-32\right):\frac{2}{3}=90\)
\(2.8\cdot x-32=90\cdot\frac{2}{3}\)
\(\frac{14}{5}x-32=60\)
\(\frac{14}{5}x=60+32\)
\(\frac{14}{5}x=92\)
\(x=\frac{230}{7}\)
B , c , d tương tự

Bài 1 :
\(a)\) Ta có :
\(3x=4y=6z\)
\(\Leftrightarrow\)\(\frac{3x}{12}=\frac{4y}{12}=\frac{6z}{12}\)
\(\Leftrightarrow\)\(\frac{x}{4}=\frac{y}{3}=\frac{z}{2}\)
\(\Leftrightarrow\)\(\frac{2x}{8}=\frac{y}{3}=\frac{5z}{10}\)
Áp dụng tính chất dãy tỉ số bằng nhau ta có :
\(\frac{2x}{8}=\frac{y}{3}=\frac{5z}{10}=\frac{2x-5z}{8-10}=\frac{-36}{-2}=18\)
Do đó :
\(\frac{x}{4}=18\)\(\Rightarrow\)\(x=18.4=72\)
\(\frac{y}{3}=18\)\(\Rightarrow\)\(y=18.3=54\)
\(\frac{z}{2}=18\)\(\Rightarrow\)\(z=18.2=36\)
Vậy \(x=72\)\(;\)\(y=54\) và \(z=36\)
Chúc bạn học tốt ~
2) Ta có: \(\frac{a}{b+c}=\frac{b}{c+a}=\frac{c}{a+b}\)
Áp dụng tính chất dãy tỉ số bằng nhau ta có:
\(\frac{a}{b+c}=\frac{b}{c+a}=\frac{c}{a+b}=\frac{a+b+c}{b+c+c+a+a+b}=\frac{a+b+c}{2.\left(a+b+c\right)}=\frac{1}{2}\)
\(\Rightarrow\frac{a}{b+c}=\frac{1}{2}\Rightarrow2a=b+c\)
\(\frac{b}{c+a}=\frac{1}{2}\Rightarrow2b=c+a\)
\(\frac{c}{a+b}=\frac{1}{2}\Rightarrow2c=a+b\)
Ta có: \(\left(1+\frac{a}{b}\right)\left(1+\frac{b}{c}\right)\left(1+\frac{c}{a}\right)=\frac{b+a}{b}.\frac{c+b}{c}.\frac{a+c}{a}=\frac{2c.2a.2b}{b.c.a}=8\)
Vậy \(\left(1+\frac{a}{b}\right)\left(1+\frac{b}{c}\right)\left(1+\frac{c}{a}\right)=8\)

\(\left(x+\frac{1}{2}\right)+\left(x+\frac{1}{4}\right)+\left(x+\frac{1}{8}\right)+\left(x+\frac{1}{16}\right)=\frac{23}{16}\)
\(4x+\frac{15}{16}=\frac{23}{16}\)
\(4x=\frac{1}{2}\)
\(x=\frac{1}{8}\)
Vậy \(x=\frac{1}{8}\)
\(\left(x+\frac{1}{2}\right)+\left(x+\frac{1}{4}\right)+\left(x+\frac{1}{8}\right)+\left(x+\frac{1}{16}\right)=\frac{23}{16}\)
\(\Rightarrow\left(x+x+x+x+x\right)+\left(\frac{1}{2}+\frac{1}{4}+\frac{1}{8}+\frac{1}{16}\right)=\frac{23}{16}\)
\(\Rightarrow5x+\frac{15}{32}=\frac{23}{16}\)
\(\Rightarrow5x=\frac{23}{16}-\frac{15}{32}\)
\(\Rightarrow5x=\frac{31}{32}\)
\(\Rightarrow x=\frac{31}{32}.\frac{1}{5}=\frac{31}{160}\)
M = (345 x (6789 + 3456 - 245)/690) x 99/100 x 98/99 x...x 2/3 x 1/2
M = ((345 x 10000)/690) x 99/2 (rút gọn)
M = (10000/2) x 99/2
M = 5000 x 99/2
M = 247500
Ok nha