Tính giá trị biểu thức: A=2 tan\(32^0\).tan\(58^o\) - si\(n^2\) \(24^o\)...

K

Khách

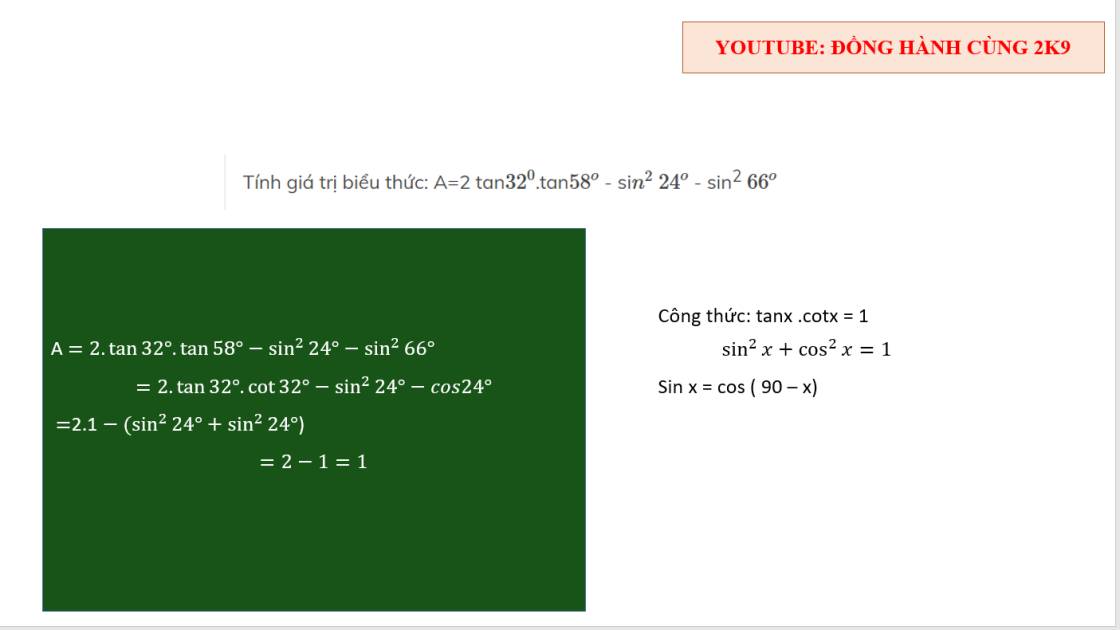
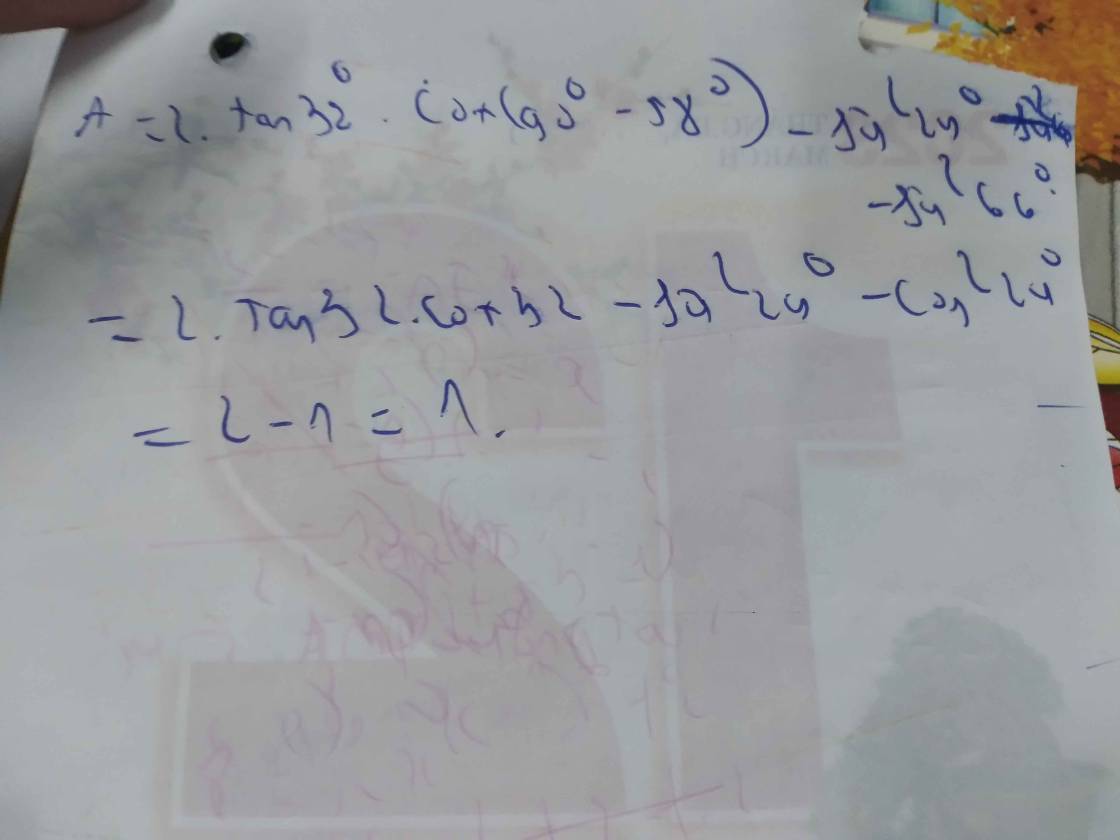
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Mua vip

N

nguyenhoangtung

4 tháng 8 2023

Tính giá trị biểu thức: A=2 tan\(32^0\).tan\(58^o\) - si\(n^2\) \(24^o\) - sin² \(66^o\)

2

NT

Nguyễn Tuấn Anh

4 tháng 8 2023

NL

Nguyễn Lê Phước Thịnh

4 tháng 8 2023

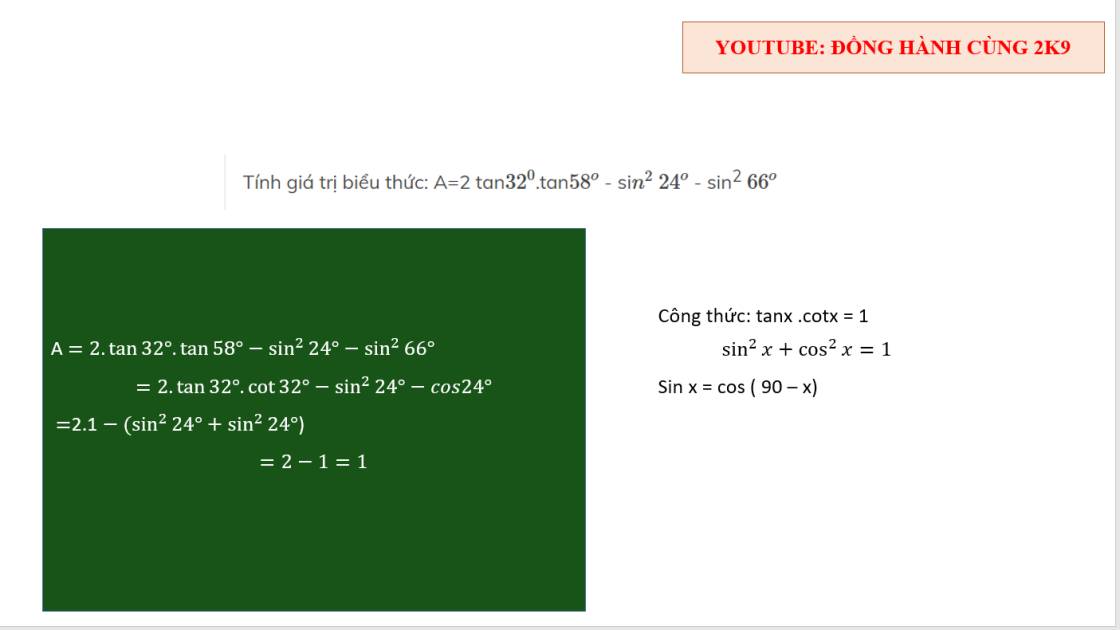
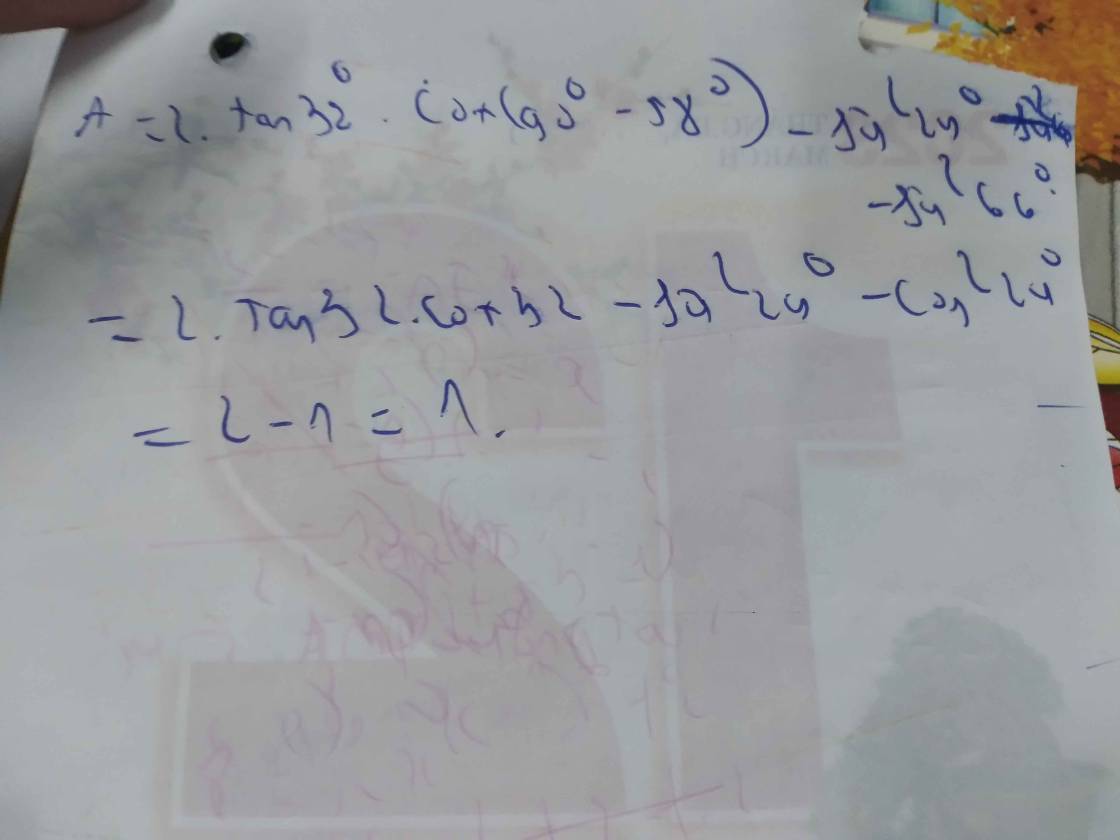
loading...

Các câu hỏi dưới đây có thể giống với câu hỏi trên

KB

Không Biết

10 tháng 11 2019

a. Cho \(\alpha\) là góc nhọn, rút gọn biểu thức :

\(A=\frac{2cos^2\alpha-1}{sin\alpha+cos\alpha}\)

b. Tính giá trị biểu thức :

P = tan 1^o.tan 2^o..... tan 88^o.tan 89^o

1

NV

Nguyễn Việt Lâm

Giáo viên

10 tháng 11 2019

\(A=\frac{2cos^2a-\left(sin^2a+cos^2a\right)}{sina+cosa}=\frac{cos^2a-sin^2a}{sina+cosa}=\frac{\left(cosa-sina\right)\left(cosa+sina\right)}{sina+cosa}=cosa-sina\)

\(P=tan1.tan89.tan2.tan88...tan44.tan46.tan45\)

\(=tan1.cot1.tan2.cot2...tan44.cot44.tan45\) (công thức \(tanx=cot\left(90^0-x\right)\))

\(=1.1.1....1=1\)

NV

Nguyễn Việt Lâm

Giáo viên

13 tháng 11 2019

\(2cos^2x-cos^2x-sin^2x=cos^2x-sin^2x\) , phép trừ của lớp 1 là \(2-1=1\) thôi mà bạn?

Còn \(tan45^0=1\) là 1 gía trị lượng giác cơ bản ai cũng nên biết chứ nhỉ? Ít nhất giá trị của các góc đặc biệt như 30 ; 45; 60; 90 cũng nên thuộc :(

QM

Quân Minh

14 tháng 8 2020 - olm

Câu hỏi hay

a) cho sin a = \(\frac{2}{3}\) . Tính giá trị của biểu thức P = tan² a - 2 cot² a

b) cho sin a.cos a =\(\frac{2\sqrt{2}}{9}\). tính giá trị đúng của biểu thức M = \(\frac{1}{\tan a+\cot a}\)

0

NT

Nguyễn Thị Bình Yên

25 tháng 7 2018

Cho 0o < x < 90o, CM các biểu thức sau không phụ thuộc vào biến: \(1.A=2\left(\sin^4x+\cos^4x+\sin^2x\cos^2x\right)^2-\left(\sin^8x+\cos^8x\right)\) \(2.B=\left(\dfrac{1-\tan^2x}{\tan x}\right)^2-\left(1+\tan^2x\right)\left(1+\cot^2x\right)\) \(3.C=\left(\sin^4x+\cos^4x-1\right)\left(\tan^2x+\cot^2x+2\right)\) \(4.D=\dfrac{\tan^2x-\cos^2x}{\sin^2x}+\dfrac{\cot^2x-\sin^2x}{\cos^2x}\) \(5.E=\dfrac{\cot^2x-\cos^2x}{\cot^2x}+\dfrac{\sin x\cdot\cos x}{\cot...

2

MP

Mysterious Person

4 tháng 9 2018

câu 1 : ta có : \(A=\left(sin^4x+cos^4x+sin^2x.cos^2x\right)^2-\left(sin^8x+cos^8x\right)\)

\(=\left(1-sin^2x.cos^2x\right)^2-\left(1-3sin^2x.cos^2x\right)\)

\(=\left(1-sin^2x.cos^2x\right)^2-\left(1-sin^2x.cos^2x\right)+2sin^2xcos^2x\)

\(=-sin^2x.cos^2x\left(1-sin^2x.cos^2x\right)+2sin^2x.cos^2x\)

\(=sin^2x.cos^2x\left(1+sin^2x.cos^2x\right)\)

tới đây mk xin sử dụng kiến thức lớp 10 một chút

\(=\dfrac{sin^22x}{4}\left(1+\dfrac{sin^22x}{4}\right)=\dfrac{sin^22x}{4}+\dfrac{sin^42x}{16}\)

vẩn phụ thuộc vào x \(\Rightarrow\) đề sai .

MP

Mysterious Person

4 tháng 9 2018

câu 1 : câu này bn có thể tìm trong trang của mk , mk nhớ đã làm nó rồi nhưng tìm hoài không đc . nếu đc bn có thể chờ mk đi hok về mk sẽ kiếm cho bn hoắc có thể là lm lại cho bn nha :)

câu 2 : https://hoc24.vn/hoi-dap/question/657072.html

câu 3 : https://hoc24.vn/hoi-dap/question/657069.html

câu 4 : https://hoc24.vn/hoi-dap/question/656635.html

câu 5 : https://hoc24.vn/hoi-dap/question/657071.html

NT

Nam Truong Van

27 tháng 9 2018

Điền vào chỗ trống {......}để đơn giản các biểu thức sau: a)\(\dfrac{ }{ }\) 1 + tan\(^2\) a =1 +\((\dfrac{...}{...})\)2 =\(\dfrac{....+....}{cos^2a}=\dfrac{........}{cos^2a}\) b) 1 + cot2 a= + \((\dfrac{...}{...})^2\) = \(\dfrac{....+....}{sin^2a}=\dfrac{....}{sin^2a}\) c) tan2 a (2 sin2a + 3 cos2 a - 2) =tan2 a[cos2 a +2 (........ +.........)-2...

2

LM

lâm mỹ ngọc

27 tháng 9 2018

a) 1 + tan22 a =1 +(\(\dfrac{sina}{cosa}\))² =\(\dfrac{sina+cosa}{cos^2a}\)=\(\dfrac{1}{cos^2a}\)

b) 1 + cot2 a= 1 +(\(\dfrac{cosa}{sina}\))² = \(\dfrac{cosa+sina}{sin^2a}\)=\(\dfrac{1}{sin^2a}\)

c) tan2 a (2 sin2a + 3 cos2 a - 2)

=tan2 a[cos2 a +2 (\(sina^2+cos^2a\))-2 ]

=\(\dfrac{sin^2a}{cos^2a}\)×\(cos^2a=sin^2a\)

NL

Nguyễn Lê Phước Thịnh

7 tháng 9 2022

b: \(1+cot^2a=1+\left(\dfrac{cosa}{sina}\right)^2=\dfrac{1}{sin^2a}\)

c: \(=tan^2a\left[2\left(1-cos^2a\right)+3cos^2a-2\right]\)

\(=tan^2a\left[cos^2a\right]\)

\(=\dfrac{sin^2a}{cos^2a}\cdot cos^2a=sin^2a\)

NT

Nguyễn Thương

12 tháng 10 2018

Chứng minh các biểu thức sau ko phụ thuộc vào góc \(\alpha\)

A= (\(\tan\alpha+\cot\alpha\))²- ( \(\tan\alpha-\cot\alpha\))²

B= sin ⁶\(\alpha+cos^6\alpha+3sin^2\alpha.cos^2\alpha\)

1

MP

Mysterious Person

12 tháng 10 2018

+) ta có : \(A=\left(tan\alpha+cot\alpha\right)^2-\left(tan\alpha-cot\alpha\right)^2\)

\(=tan^2\alpha+cot^2\alpha+2-tan^2\alpha-cot^2\alpha+2=4\) (không phụ thuộc vào \(\alpha\)) \(\Rightarrow\) (đpcm)

+) ta có : \(B=sin^6\alpha+cos^6\alpha+3sin^2\alpha.cos^2\alpha\)

\(=\left(sin^2\alpha\right)^3+\left(cos^2\alpha\right)^3+3sin^2\alpha.cos^2\alpha\)

\(=\left(sin^2\alpha+cos^2\alpha\right)\left(sin^4\alpha+cos^4\alpha-sin^2\alpha.cos^2\alpha\right)+3sin^2\alpha.cos^2\alpha\)

\(=\left(\left(sin^2\alpha+cos^2\alpha\right)^2-3sin^2\alpha.cos^2\alpha\right)+3sin^2\alpha.cos^2\alpha\)

\(=1\) (không phụ thuộc vào \(\alpha\) ) \(\Rightarrow\) (đpcm)

ML

My Le Tra

10 tháng 8 2019

Tính

A=\(\tan^2\alpha+\sin^2\alpha-\cot\)(90^o-α)-\(\cos^2\)(90^o-α)

B=(\(\sin^2-\cos^2\))²+4\(\sin\alpha.\cos\alpha\)

0

HN

Huỳnh Nguyên

26 tháng 6 2018

1. cho x là góc nhọn, chứng minh \(\dfrac{1}{\sin^2}x\) - 1 = \(\dfrac{1}{\tan^2x}\) 2. cho \(\cos x=\dfrac{1}{3}\); tính giá trị của \(A=\dfrac{1}{\cot^2x}+1\) 3. đơn giản biểu thức: \(\tan^2\alpha-\sin^2\alpha.\tan^2\alpha\) 4.cho 00 < 900, c/m...

2

AH

Akai Haruma

Giáo viên

27 tháng 6 2018

Hỏi đáp Toán

AH

Akai Haruma

Giáo viên

27 tháng 6 2018

Hỏi đáp Toán

QM

Quân Minh

13 tháng 8 2020

a) cho sin a = \(\frac{2}{3}\) . Tính giá trị của biểu thức P = tan² a - 2 cot²a

b) cho sin a.cos a =\(\frac{2\sqrt{2}}{9}\). tính giá trị đúng của biểu thức M = \(\frac{1}{\tan a+\cot a}\)

1

NV

Nguyễn Việt Lâm

Giáo viên

14 tháng 8 2020

a/ \(cos^2a=1-sin^2a=\frac{5}{9}\)

\(P=\frac{sin^2a}{cos^2a}-\frac{2cos^2a}{sin^2a}=\frac{\frac{4}{9}}{\frac{5}{9}}-\frac{\frac{10}{9}}{\frac{4}{9}}=-\frac{17}{10}\)

b/ \(M=\frac{1}{\frac{sina}{cosa}+\frac{cosa}{sina}}=\frac{1}{\frac{sin^2a+cos^2a}{sina.cosa}}=sina.cosa=\frac{2\sqrt{2}}{9}\)

NL

Nguyễn Lê Ngọc Quang

20 tháng 10 2017

Câu 1: Cho hai góc nhọn phụ nhau A và B. Hệ thức nào sau đây không đúng ? A. Sin A = Cos(90o -B) B. Sin A = Cos B C. Tan A - cot B = 0 D. Tan A.tan B = 1 Câu 2: Cho \(\alpha+\beta=90^o\) , ta có: A. \(\sin\alpha=\sin\beta\) B. \(\tan\alpha.\cot\alpha=\dfrac{\sqrt{2}}{2}\) C. \(\sin^2\alpha+\cos^2\beta=1\) D. \(\tan\alpha=\dfrac{\cos\beta}{\cos\alpha}\) Câu 3: Cho tam giác ABC vuông tại A có AB = 10cm, góc ACB =40o a) Tính độ dài BC...

0