Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Để tính độ dài cạnh kề với cạnh có độ dài bằng 4, ta có thể sử dụng định lý Pythagoras. Định lý này cho biết rằng trong một tam giác vuông, bình phương của độ dài cạnh huyền (đường chéo dài nhất) bằng tổng bình phương của độ dài hai cạnh góc vuông.
Trong trường hợp này, ta có độ dài hai đường chéo là 6 và 8. Để tìm độ dài cạnh kề với cạnh có độ dài bằng 4, ta cần tìm độ dài cạnh còn lại của hình bình hành.
Áp dụng định lý Pythagoras, ta có: (độ dài cạnh kề)^2 + (độ dài cạnh kề)^2 = (độ dài đường chéo)^2
Đặt độ dài cạnh kề là x, ta có: x^2 + 4^2 = 6^2
Giải phương trình trên, ta có: x^2 + 16 = 36 x^2 = 36 - 16 x^2 = 20 x = √20
Vậy độ dài cạnh kề với cạnh có độ dài bằng 4 là √20.

Đáp án: A
Gọi chiều dài, chiều rộng của mảnh vườn lần lượt là ![]() (m)
(m) ![]()
Theo đề bài ta có:
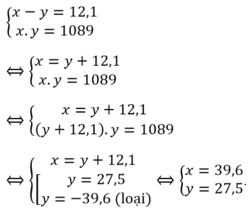

BH là đường cao nên cũng là đường trung trực của tam giác ABC đều
\(\Rightarrow BH\perp AC\) tại H cũng là trung điểm của BC
\(\Rightarrow AH=HC=\dfrac{1}{2}AC=\dfrac{3}{2}a\)
Vì \(\Delta AHB\) vuông tại H nên \(BH=\sqrt{AB^2-AH^2}=\sqrt{9a^2-\dfrac{9}{4}a^2}=\dfrac{3a\sqrt{3}}{2}\)
\(S_{ABC}=\dfrac{1}{2}BH\cdot AC=\dfrac{1}{2}\cdot\dfrac{3a\sqrt{3}}{2}\cdot3a=\dfrac{9a^2\sqrt{3}}{4}\left(đvdt\right)\)

a: AB=20cm; AH=(25+20)/2=22,5m
S=22,5^2=506,25m2
b: Xét tứ giác ABMC có
AB//MC
AB=MC
=>ABMC là hbh
=>S ABI=S CMI
c: BI/IC=1

Lời giải:
Gọi bán kính đáy của hình trụ là $r$ thì chiều cao $h=4r$
Diện tích xung quanh: $S_{xq}=2\pi rh =2r.4r\pi = 8r^2\pi = 288\pi$
$\Rightarrow r^2=36\Rightarrow r=6$ (cm)

S A B C D H P A' B' C' D' P' H
Giả sử các cạnh bên của hình chóp cắt nhau tại S.
Họi H và H lần lượt là tâm đường trong ngoại tiếp các hình vuông ABCD và A'B'C'D'
Thì S, H, H' thẳng hàng và AH, SH' lần lượt là các đường cao của các hình chóp S.ABCD và S.A'B'C'D'
Gọi P là trung điểm của BC, P' là trung điểm của B'C'
Ta có SP và SP' là các trung đoạn của các hình chóp đều S.ABCD và S.A'B'C'D'
Xét tam giác SHP vuông tại H nên \(SP=\sqrt{SH^2+HP^2}=\sqrt{3^2+4^2}=5\left(cm\right)\)
Vì B'C' vuông góc với BC và B'C'=1/2B'C' là đường trung bình của tam giác SBC
Do đó : \(SH'=\frac{1}{2}SH=2cm;SP'=\frac{1}{2}SP=2,5cm\)
Thể tích hình chóp S.ABCD là
\(V_1=\frac{1}{3}SH.BC^2=\frac{1}{3}.4.6^2=48cm^3\)
Thể tích hình chóp S.A'B'C'D' là
\(V_2=\frac{1}{3}SH'.A'B'^2=\frac{1}{3}.2.3^2=48-6=42cm^3\)
Thể tích của hình chóp cụt là : \(V=V_1-V_2=48-6=42cm^3\)
Diện tích xung quanh của hình chóp cụt là :
\(S_{xq}=AB^2+A'B'^2+4\frac{PP'\left(AB+A'B'\right)}{2}=6^2+3^2+4\frac{2,5\left(6+3\right)}{2}=90cm^2\)

Gọi O là giao của hai đường chéo
Ta có: \(\overrightarrow{AB}=\overrightarrow{AO}+\overrightarrow{OB}\); \(\overrightarrow{AD}=\overrightarrow{AO}+\overrightarrow{OD}=\overrightarrow{AO}-\overrightarrow{OB}\)
Suy ra : \(\overrightarrow{AB}.\overrightarrow{AD}=AO^2-OB^2=3^2-4^2=-7\)
\(\Leftrightarrow AB^2.AD^2=49\)\(\Leftrightarrow AD^2=\dfrac{49}{16}\Leftrightarrow AD=\dfrac{7}{4}\)


Chiều cao là:
(25-7):2=9 (cm)
Cạnh đáy là:
9+7=16 (cm)
diện tích hình bình hành là:
16x9=144 (cm2)
đ/s :
Chiều cao hình bình hành là :
( 25 - 7 ) : 2 = 9 ( cm )
Cạnh đáy hình bình hành là :
25 - 9 = 16 ( cm )
diện tích hình bình hành là :
16 x 9 = 144 ( cm2 )
Đáp số : 144 cm2