K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
S
11 tháng 4 2017
Đề bài: Tìm đạo hàm cấp hai của hàm số sau:
\(y=cos^2x\)
Lời giải:
\(y'=2cosx.\left(cosx\right)'=2cosx.\left(-sinx\right)=-2sinx.cosx=-sin2x\)
\(y"=-\left(2x\right)'.cos2x=-2cos2x\)
BT
26 tháng 5 2017
\(y'\left(x\right)=x'cos2x+\left(cos2x\right)'.x\)\(=cos2x-2sin2x.x\)
\(y''\left(x\right)=\left(cos2x-2xsin2x\right)'\)\(=-2sin2x-\left(2sin2x-2x.\left(-cos2x\right).2\right)\)
\(=-2sin2x-2sin2x-4xcos2x\)
\(=-4sin2x-4xcos2x\).
\(=-4\left(sin2x+xcos2x\right)\).
SG
0
PT
1
PT
1
CM
8 tháng 10 2019
Chọn D
y ' = sin 2 x + cos 2 x / . 2 sin 2 x − cos 2 x − 2 sin 2 x − cos 2 x / . sin 2 x + cos 2 x 2 sin 2 x − cos 2 x 2
y ' = 2 cos 2 x − 2 sin 2 x 2 sin 2 x − cos 2 x − 4 cos 2 x + 2 sin 2 x sin 2 x + cos 2 x 2 sin 2 x − cos 2 x 2 = 4. c os2x. sin2x - 2cos 2 2 x − 4 sin 2 2 x + 2. sin 2 x . c os2x ( 2 sin 2 x − cos 2 x ) 2 − ( 4cos2x . sin2x + 4cos 2 2 x + 2 sin 2 2 x + 2 sin 2 x . c os2x ( 2 sin 2 x − c os2x) 2
y ' = − 6 cos 2 2 x − 6 sin 2 2 x 2 sin 2 x − cos 2 x 2 = − 6 2 sin 2 x − cos 2 x 2
PT
1
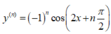
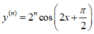
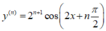
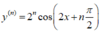
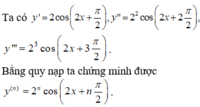
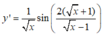
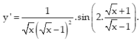
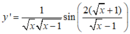
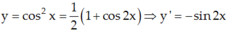
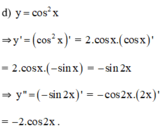
y = cos (2x)
y' = (2x)'.(-sin(2x))
y' = -2sin(2x)
Vậy y' = -2sin(2x)