Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a: \(y'=\left(x^2\right)'+\left(3x\right)'-\left(6x^6\right)'+\left(\dfrac{2x-3}{x-1}\right)'\)
\(=2x+3-6\cdot6x^5+\dfrac{\left(2x-3\right)'\left(x-1\right)-\left(2x-3\right)\left(x-1\right)'}{\left(x-1\right)^2}\)
\(=-36x^5+2x+3+\dfrac{2\left(x-1\right)-2x+3}{\left(x-1\right)^2}\)
\(=-36x^5+2x+3+\dfrac{1}{\left(x-1\right)^2}\)
b: \(\left(\sqrt{2x^2-3x+1}\right)'=\dfrac{\left(2x^2-3x+1\right)'}{2\sqrt{2x^2-3x+1}}\)
\(=\dfrac{4x-3}{2\sqrt{2x^2-3x+1}}\)
\(y'=3\cdot2x-4+\dfrac{4x-3}{2\sqrt{2x^2-3x+1}}\)
\(=6x-4+\dfrac{4x-3}{2\sqrt{2x^2-3x+1}}\)
c: \(\left(\sqrt{4x^2-3x+1}\right)'=\dfrac{\left(4x^2-3x+1\right)'}{2\sqrt{4x^2-3x+1}}\)
\(=\dfrac{8x-3}{2\sqrt{4x^2-3x+1}}\)
\(y'=\left(\sqrt{4x^2-3x+1}\right)'-4'=\dfrac{8x-3}{2\sqrt{4x^2-3x+1}}\)

a. \(y'=\dfrac{-1}{\left(x-1\right)}\)
b. \(y'=\dfrac{5}{\left(1-3x\right)^2}\)
c. \(y=\dfrac{\left(x+1\right)^2+1}{x+1}=x+1+\dfrac{1}{x+1}\Rightarrow y'=1-\dfrac{1}{\left(x+1\right)^2}=\dfrac{x^2+2x}{\left(x+1\right)^2}\)
d. \(y'=\dfrac{4x\left(x^2-2x-3\right)-2x^2\left(2x-2\right)}{\left(x^2-2x-3\right)^2}=\dfrac{-4x^2-12x}{\left(x^2-2x-3\right)^2}\)
e. \(y'=1+\dfrac{2}{\left(x-1\right)^2}=\dfrac{x^2-2x+3}{\left(x-1\right)^2}\)
g. \(y'=\dfrac{\left(4x-4\right)\left(2x+1\right)-2\left(2x^2-4x+5\right)}{\left(2x+1\right)^2}=\dfrac{4x^2+4x-14}{\left(2x+1\right)^2}\)
2.
a. \(y'=4\left(x^2+x+1\right)^3.\left(x^2+x+1\right)'=4\left(x^2+x+1\right)^3\left(2x+1\right)\)
b. \(y'=5\left(1-2x^2\right)^4.\left(1-2x^2\right)'=-20x\left(1-2x^2\right)^4\)
c. \(y'=3\left(\dfrac{2x+1}{x-1}\right)^2.\left(\dfrac{2x+1}{x-1}\right)'=3\left(\dfrac{2x+1}{x-1}\right)^2.\left(\dfrac{-3}{\left(x-1\right)^2}\right)=\dfrac{-9\left(2x+1\right)^2}{\left(x-1\right)^4}\)
d. \(y'=\dfrac{2\left(x+1\right)\left(x-1\right)^3-3\left(x-1\right)^2\left(x+1\right)^2}{\left(x-1\right)^6}=\dfrac{-x^2-6x-5}{\left(x-1\right)^4}\)
e. \(y'=-\dfrac{\left[\left(x^2-2x+5\right)^2\right]'}{\left(x^2-2x+5\right)^4}=-\dfrac{2\left(x^2-2x+5\right)\left(2x-2\right)}{\left(x^2-2x+5\right)^4}=-\dfrac{4\left(x-1\right)}{\left(x^2-2x+5\right)^3}\)
f. \(y'=4\left(3-2x^2\right)^3.\left(3-2x^2\right)'=-16x\left(3-2x^2\right)^3\)

a: \(y'=\dfrac{\left(x^2+3x-1\right)'\cdot\left(x+2\right)-\left(x^2+3x-1\right)\cdot\left(x+2\right)'}{\left(x+2\right)^2}\)
\(=\dfrac{\left(2x+3\right)\left(x+2\right)-\left(x^2+3x-1\right)}{\left(x+2\right)^2}\)
\(=\dfrac{2x^2+7x+6-x^2-3x+1}{\left(x+2\right)^2}=\dfrac{x^2+4x+7}{\left(x+2\right)^2}\)
b: \(y'=\dfrac{\left(2x^2-x\right)'\cdot\left(x^2+1\right)-\left(2x^2-x\right)\left(x^2+1\right)'}{\left(x^2+1\right)^2}\)
\(=\dfrac{4x\left(x^2+1\right)-2x\left(2x^2-x\right)}{\left(x^2+1\right)^2}\)
\(=\dfrac{4x^3+4x-4x^3+2x^2}{\left(x^2+1\right)^2}=\dfrac{2x^2+4x}{\left(x^2+1\right)^2}\)
c: \(\left(\dfrac{3-2x}{x-1}\right)'=\dfrac{\left(3-2x\right)'\left(x-1\right)-\left(3-2x\right)\left(x-1\right)'}{\left(x-1\right)^2}\)
\(=\dfrac{-2\left(x-1\right)-\left(3-2x\right)}{\left(x-1\right)^2}=\dfrac{-2x+2-3+2x}{\left(x-1\right)^2}=-\dfrac{1}{\left(x-1\right)^2}\)
\(\left(\sqrt{2x-3}\right)'=\dfrac{\left(2x-3\right)'}{2\sqrt{2x-3}}=\dfrac{1}{\sqrt{2x-3}}\)
\(y'=\left(\dfrac{3-2x}{x-1}\right)'+\left(\sqrt{2x-3}\right)'\)
\(=\dfrac{-1}{\left(x-1\right)^2}+\dfrac{1}{\sqrt{2x-3}}\)

a) =
=
.
b) =
=
.
c) =
=
.
d) y' =\(\dfrac{\left(x^2+7x+3\right)'\left(x^2-3x\right)-\left(x^2+7x+3\right)\left(x^2-3x\right)'}{\left(x^2-3x\right)^2}\)=\(\dfrac{\left(2x+7\right)\left(x^2-3x\right)-\left(x^2+7x+3\right)\left(2x-3\right)}{\left(x^2-3x\right)^2}\)=\(\dfrac{-2x^2-6x+9}{\left(x^2-3x\right)^2}\)

a) Đặt \(u = 3{\rm{x}}\) thì \(y = \sin u\). Ta có: \(u{'_x} = {\left( {3{\rm{x}}} \right)^\prime } = 3\) và \(y{'_u} = {\left( {\sin u} \right)^\prime } = \cos u\).
Suy ra \(y{'_x} = y{'_u}.u{'_x} = \cos u.3 = 3\cos 3{\rm{x}}\).
Vậy \(y' = 3\cos 3{\rm{x}}\).
b) Đặt \(u = \cos 2{\rm{x}}\) thì \(y = {u^3}\). Ta có: \(u{'_x} = {\left( {\cos 2{\rm{x}}} \right)^\prime } = - 2\sin 2{\rm{x}}\) và \(y{'_u} = {\left( {{u^3}} \right)^\prime } = 3{u^2}\).
Suy ra \(y{'_x} = y{'_u}.u{'_x} = 3{u^2}.\left( { - 2\sin 2{\rm{x}}} \right) = 3{\left( {\cos 2{\rm{x}}} \right)^2}.\left( { - 2\sin 2{\rm{x}}} \right) = - 6\sin 2{\rm{x}}{\cos ^2}2{\rm{x}}\).
Vậy \(y' = - 6\sin 2{\rm{x}}{\cos ^2}2{\rm{x}}\).
c) Đặt \(u = \tan {\rm{x}}\) thì \(y = {u^2}\). Ta có: \(u{'_x} = {\left( {\tan {\rm{x}}} \right)^\prime } = \frac{1}{{{{\cos }^2}x}}\) và \(y{'_u} = {\left( {{u^2}} \right)^\prime } = 2u\).
Suy ra \(y{'_x} = y{'_u}.u{'_x} = 2u.\frac{1}{{{{\cos }^2}x}} = 2\tan x\left( {{{\tan }^2}x + 1} \right)\).
Vậy \(y' = 2\tan x\left( {{{\tan }^2}x + 1} \right)\).
d) Đặt \(u = 4 - {x^2}\) thì \(y = \cot u\). Ta có: \(u{'_x} = {\left( {4 - {x^2}} \right)^\prime } = - 2{\rm{x}}\) và \(y{'_u} = {\left( {\cot u} \right)^\prime } = - \frac{1}{{{{\sin }^2}u}}\).
Suy ra \(y{'_x} = y{'_u}.u{'_x} = - \frac{1}{{{{\sin }^2}u}}.\left( { - 2{\rm{x}}} \right) = \frac{{2{\rm{x}}}}{{{{\sin }^2}\left( {4 - {x^2}} \right)}}\).
Vậy \(y' = \frac{{2{\rm{x}}}}{{{{\sin }^2}\left( {4 - {x^2}} \right)}}\).

tham khảo:
a)\(y'=xsin2x+sin^2x\)
\(y'=sin^2x+xsin2x\)
b)\(y'=-2sin2x+2cosx\\ y'=2\left(cosx-sin2x\right)\)
c)\(y=sin3x-3sinx\)
\(y'=3cos3x-3cosx\)
d)\(y'=\dfrac{1}{cos^2x}-\dfrac{1}{sin^2x}\)
\(y'=\dfrac{sin^2x-cos^2x}{sin^2x.cos^2x}\)


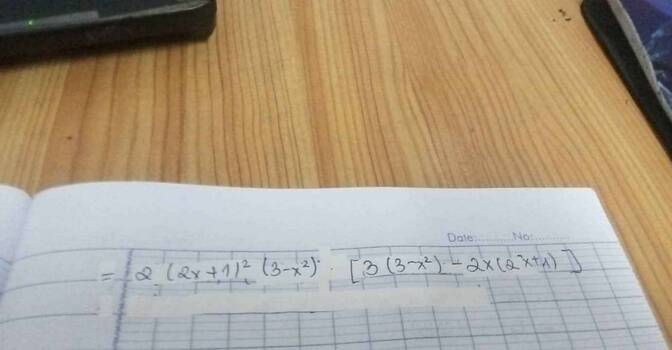
a) ta có : \(\left(y\right)'=\left(x^4-3x^3+\sqrt{\dfrac{x-3}{4}}\right)'=\left(x^4-3x^3+\left(\dfrac{x-3}{4}\right)^{0,5}\right)'\)
\(=\left(x^4\right)'-\left(3x^3\right)'+\left(\left(\dfrac{x-3}{4}\right)^{0,5}\right)'=4x^3-9x^2+\dfrac{1}{2}\left(\dfrac{x-3}{4}\right)^{-0,5}\)
\(=4x^3-9x^2+\dfrac{1}{2\sqrt{\dfrac{x-3}{4}}}\)
câu b với câu c ; mk o hiểu cái đề